Критерий существования седловых точек

Теорема

Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях.

Доказательство:

Так как функция α(Р) непрерывна на компакте S_A, то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях:

Аналогичным образом обосновывается существование и верхней цены игры в смешанных стратегиях.

 

Критерий существования седловых точек

Седловым элементом матрицы называется элемент, являющийся минимальным в своей строке и максимальным в своем столбце.

Ситуацию (s*, t*) назовем седловой точкой игры G = < S, T, j>, если

" s Î S " t Î T j(s, t*) £ j(s*, t*) £ j(s*, t). (3)

Теорема 2 (критерий существования седловой точки).

Для того, чтобы матричная игра G = < S, T, j> имела седловые точки необходимо и достаточно, чтобы были равны величины a и b.

Доказательство.

Необходимость.

Пусть (s*, t*) – седловая точка, т. е. выполнено (3).

1) Так как j(s_i, t*) £ j(s*, t*), а j(s*, t*) – число, то

,

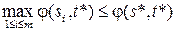а отсюда следует (берем минимум по j, от которого левая часть не зависит), что

(4)

2) Так как j(s*, t*) £ j(s*, t_j), а j(s*, t*) – число, то

,

а отсюда следует, что

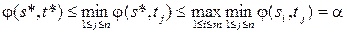(5)

3) Объединяя (4) и (5), получаем b £ j(s*, t*) £ a.

Поскольку по теореме о минимаксе и максимине a £ b, то a = b.

Замечание 1.

В равенстве (3) s* и t* максиминная и минимаксная стратегии соответственно.

Достаточность.

Пусть выполнено a = b, т. е. .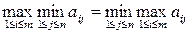

Обозначим

s* Î S: ,

t* Î T: .

Докажем, что (s*, t*) – седловая точка.

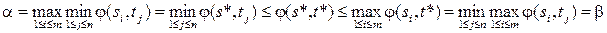
(а) (б)

Поскольку a = b, то в последней цепочке все неравенства выполняются в виде равенств. Следовательно, получаем:

Из (а): " j

Из (б): " i

Последние два неравенства и дают (3).

Теорема доказана.

 

Вопрос 12.

Цена игры в смешанных стратегиях. Стратегии, оптимальные во множестве смешанных стратегий. Полное (общее) и частное решения игры в смешанных стратегиях. Основная теорема теории игр Дж. фон Неймана.

Если нижняя и верхняя 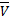цены игры в смешанных стратегиях совпадают, то их общее значение V= = 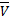называется ценой игры в смешанных стратегиях. Нижняя и верхняя цены игры в чистых стратегиях α и β и цены игры в смешанных стратегиях V связаны между собой неравенствами α≤V≤β.

Стратегии P^O и Q^O соответственно игроков А и В, удовлетворяющие равенствам V=α(P^O)=β(Q^O) (и тогда это общее значение очевидно равно H(P^O,Q^O)), называется оптимальными смешанными стратегиями игроков А и В.

Таким образом, оптимальные смешанные (в частности, чистые) стратегии P^O и Q^O соответственно игроков А и В обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.

Множество оптимальных смешанных стратегий соответственно игроков А и В обозначим через (S_A)^О и (S_B)^О.

Полным решением игры в смешанных стратегиях называется трехэлементная совокупность {(S_A)^O,(S_B)^O,V}. Любая пара оптимальных стратегий P^O и Q^O соответственно игроков А и В и цена игры в смешанных стратегиях V образуют частное решение в смешанных стратегиях.

Основная теорема теории игр Дж. фон Неймана:

Любая матричная игра имеет решение в смешанных стратегиях, т.е. существует цена игры в смешанных стратегиях V и оптимальные смешанные стратегии P^O и Q^O соответственно игроков А и В, т.е.

V= =

 

Вопрос 13

Критерии оптимальных смешанных стратегий в терминах данной цены игры, выигрыш-функции и множеств смешанных стратегий игроков.

Теорема. (Критерии оптимальных стратегий).

Пусть V-цена игры, H(P,Q) – выигрыш-функция, S_A и S_B – множества смешанных стратегий соответственно игроков А и В.

1. Для того чтобы стратегия Р^О игрока А была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство:

H(P^О,Q)≥V

Для любого Q ϵ S_B, т.е. выбор игроком А оптимальной стратегии Р^О гарантирует ему выигрыш H(P^О,Q), не меньший цены игры V, при любой стратегии Q игрока В.

2. Для того чтобы стратегия Q^O игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

H(P^О,Q)≤V

Для любого Р ϵ S_А , т.е. выбор игроком В оптимальной стратегии Q^О гарантирует ему проигрыш H(P,Q^О), не больший цены игры V, при любой стратегии Р игрока А.

Данная теорема остаётся справедливой, если в её формулировке множество смешанных стратегий S_A и S_B заменить соответственно на множество чистых стратегий S^С_A и S^С_B.

Доказательство:

Утверждение 1:

Необходимость:

Пусть Р⁰ – оптимальная стратегия игрока А. тогда по теореме фон Неймана показатель эффективности стратегии Р⁰ равен цене игры V:

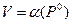(1)

Рассматривая как показатель эффективности стратегии Р⁰ относительно множества S _B смешанных стратегий игрока В, будем иметь по определению:

(2)

Из равенств (1) и (2) получаем неравенство H(P^О,Q)≥V

Достаточность:

Пусть для некоторой стратегии Р0 игрока А выполняется неравенство H(P^О,Q)≥V. Для доказательство оптимальности стратегии Р0 достаточность показать справедливость равенства

Так как неравенство выполняется для любой стратегии игрока В, то

(3)

Но цена игры V равна нижней цене игры V, по определению которой

(4)

Совокупность (3) и (4) эквивалентна равенству . Достаточность доказана

Утверждение 2:

АНАЛОГИЧНЫЕ РАССЖУДЕНИЯ.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: