 |
Критерий (крайнего пессимизма) Вальда оптимальности чистых и смешанных стратегий.
|
|
|
|
Критерий Вальда – частный случай обобщенного критерия Гурвица относительно выигрышей со специальными коэффициентами λ1=1,λ2=…=λn=0.
Подставляя значения коэффициентов в Gi(λ1,λ2,…,λn)= 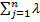 jbij, i=1,…,m и учитывая bi1 =
jbij, i=1,…,m и учитывая bi1 = 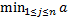 ij, i=1,…,m, получим показатель эффективности стратегии Ai по критерию Вальда:
ij, i=1,…,m, получим показатель эффективности стратегии Ai по критерию Вальда:
Wi = Gi(1,0,…,0)=bi1= 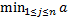 ij , i=1,…,m,
ij , i=1,…,m,
Представляющий собой минимальный выигрыш игрока А при применении им стратегии Ai. Оптимальной среди чистых стратегий по критерию Вальда явл.,таким образом, стратегия Ai0, имеющая максимальный показатель эффективности Wi. . т.е.: Wi0 = W = 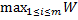 I =
I = 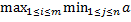 ij
ij
Другими словами, оптимальной среди чистых стратегий по критерию Вальда считается та чистая стратегия, при которой минимальный выигрыш явл максимальным среди минимальных выигрышей всех чистых стратегий. И получаем, что для критерия Вальда показатель пессимизма λр=1, а показатель оптимизма λ0=0. Это говорит о том, что критерий Вальда явл критерием крайнего пессимизма, ибо ориентирует игрока А на наихудшие для него состояния природы.
Максимаксный критерий (крайнего оптимизма) оптимальности чистых и смешанных стратегий.
Это противоположность критерию Вальда.Это частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэф-ты выбираются так:
λ1=…=λn-1= 0,λn=1.
Если эти коэф-ты подставить в Gi(λ1,λ2,…,λn)= 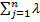 jbij, i=1,…,m и учесть bin =
jbij, i=1,…,m и учесть bin =  ij, i=1,…,m, то получим формулу для показателя эффективности стратегии Ai по максимаксному критерию:
ij, i=1,…,m, то получим формулу для показателя эффективности стратегии Ai по максимаксному критерию:
Mi = Gi(0,0,…,0,1)=bin=  ij , i=1,…,m,
ij , i=1,…,m,
Значит, в качестве показателя эффективности стратегии Aiпо максимаксному критерию выбирается максимальный выигрыш при этой стратегии. Тогда оптимальной среди чистых стратегий поксимаксному критерию явл стратегия Ai0 с максимальным показателем эффективности:
|
|
|
Mi0 = M = 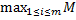 I =
I = 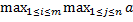 ij
ij
Т.е стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. Можно сказать, что оптимальной будет та чистая стратегия, при которой (хотя бы) один из выигрышей явл максимальным среди выигрышей всех чистых стратегий.
Таким образом, максимаксный критерий явл критерием крайнего оптимизма, тк ориентирует лицо, принимающее решение (игрока А), на наилучшие для него состояния природы и, как следствие отсюда, - на порой неоправданно легкомысленное поведение при выборе стратегий.
Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
Критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателями оптимизма lÎ[0,1]. Данный критерий явл.-ся как бы промежуточным между критериями крайнего пессимизма и крайнего оптимизма и представляет собой частный случай обощенного критерия Гурвица относительно выигрышей с коэффициентами
λ1=1-λ, λ2=…=λn-1=0, λn=λ
Показателем эффективности стратегии Ai по рассматриваемому критерию явл.-ся величина
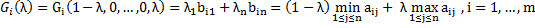
Оптимальной же стратегией по этому критерию считается стратегия Ai0 с максимальным показателем эффективности
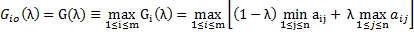
Вообще показатели пессимизма и оптимизма в этом критерии равны соответственно λp =1- λ и λ0 = λ. При λ=0 мы получаем критерий Вальда, а при λ=1 – максимаксный критерий. Чем ближе к нулю показатель оптимизма λ, тем ближе к единице показатель пессимизма 1- λ, и тем меньше оптимизма и больше пессимизма. И наоборот, чем ближе λ к единиче, тем больше оптимизма и меньше пессимизма.
Вопрос 21
«Критерий Сэвиджа».
Или КРИТЕРИЙ КРАЙНЕГО ПЕССИМИЗМА – представляет собой частный случай обобщенного критерия Гурвица относительно рисков с коэффициентами.
|
|
|
Показатель неэффективности: 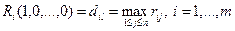 - максимальный риск при выборе игроком А стратегии Аi.
- максимальный риск при выборе игроком А стратегии Аi.
Оптимальной среди чистых стратегий по критерию Сэвиджа является в соответствии с 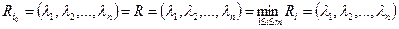 стратегия
стратегия 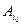 с минимальным показателем неэффективности
с минимальным показателем неэффективности 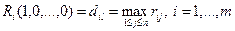 , то есть:
, то есть:  .
.
Таким образом, оптимальной среди чистых стратегий по критерию Сэвиджа считается та чистая стратегия, максимальный риск при выборе которой является минимальным среди максимальных рисков всех чистых стратегий. Поэтому оптимальная стратегий по критерию Сэвиджа гарантирует игроку А при любых состояниях природы риск, не больший, чем минимакс 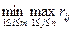
Для критерия Сэвиджа показатель пессимизма из 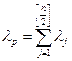 и
и 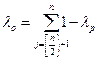 , а также λ1=1, λ2=…= λn=0 получаем, что
, а также λ1=1, λ2=…= λn=0 получаем, что 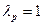 , а показатель оптимизма
, а показатель оптимизма 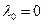 . Поэтому критерий Сэвиджа является критерием крайнего пессимизма. Он предполагает наихудшие для игрока А состояния природы, при которых риск каждой из чистых стратегий максимален.
. Поэтому критерий Сэвиджа является критерием крайнего пессимизма. Он предполагает наихудшие для игрока А состояния природы, при которых риск каждой из чистых стратегий максимален.
Отметим, что и критерий Вальда и критерий Сэвиджа являются критериями крайнего пессимизма, но все же они не являются эквивалентными
|
|
|


