Активность радионуклида. Единицы активности

Таблица 1.1

Рекомендуемые значения КК для излучения с неизвестным энергетическим составом, Зв/Гр

 

Вид излучения	КК
Рентгеновское и гамма-излучение, β - излучение позитроны
Нейтроны с энергией меньше 20 кэВ
Нейтроны с энергией 0,1 МэВ - 10 МэВ
Протоны с энергий меньше 10 МэВ
Альфа-излучение с энергией меньше 10 МэВ
Тяжелые ядра отдачи

 

Эквивалентная доза и.и. H — это произведение поглощенной дозы Д на коэффициент качества

H = кк ∙ Д. (1.15)

Единица эквивалентной дозы СИ — зиверт (Зв). Зиверт равен эквивалентной дозе, при которой произведение поглощенной дозы в биологической ткани стандартного состава на кк равно 1 Дж/кг. Иначе говоря, зиверт — единица эквивалентной дозы любого вида излучения в биологической ткани, которое создает такой же биологический эффект, как и поглощенная доза в 1 Гр образцового (кк = 1) рентгеновского или гамма-излучения.

Внесистемная единица эквивалентной дозы — бэр (биологический эквивалент рада). Бэр равен эквивалентной дозе, при которой произведение поглощенной дозы в биологической ткани на кк равно 100 эрг/г. Т. е. бэр — единица эквивалентной дозы излучения любого вида в биологической ткани, которое создает такой же биологический эффект, как и поглощенная доза в 1 рад образцового рентгеновского или гамма- излучения. Таким образом, 1 бэр = 0,01 Зв.

Биологическая ткань стандартного состава, рекомендованная ГОСТ, содержит кислород - 76 %, водорода - 10,1 %, углерода - 11,1 %, азота - 2,6 % по массовому составу.

Согласно определению Н (1.15) КК имеет размерность Зв/Гр. В заключении отметим, что понятие эквивалентной дозы обычно используется при облучении человека малыми дозами (дозами не превышающими пяти предельно допустимых годовых доз). Это означает, что при больших значениях поглощенных доз Д КК всех видов излучения следует принять равным единице, т. е. кк оказывается зависящим также и от величины поглощенной дозы Д.

Действующими в РФ «Нормами радиационной безопасности, НРБ-99» все население делится на три категории облучаемых лиц:

1. Категория А — персонал, т. е. лица, работающие с источниками и.и.;

2. Категория Б — ограниченная часть населения, т. е. лица, которые непосредственно с источниками и.и. не работают, но по условиям проживания или размещения рабочих мест могут подвергаться воздействию излучения;

3. Категория В — население края, области страны.

Для оценки опасности или безопасности того или иного радиационного воздействия излучений на человека, дозу облучения необходимо сопоставлять с некоторым ее значением, которое являлось бы мерой опасности. Согласно НРБ-99 такими значениями являются основные дозовые пределы:

— предельно допустимая доза (ПДД), равная 5 бэр для лиц категории А;

— предел дозы (ПД), равной 0,5 бэр для лиц категории Б;

— облучение лиц категории В не регламентируется, т. к. оно должно быть на уровне фона.

ПДД — это наибольшее значение индивидуальной эквивалентной дозы за год, которая при равномерном воздействии в течение 50 лет не вызовет в состоянии здоровья профессионального работника неблагоприятных изменений.

ПД — предельная эквивалентная доза за год для ограниченной части населения. ПД < ПДД.

Значения ПДД и ПД установлены в предположении беспорогового воздействия и.и. на организм человека, т. е. в предположении, что никакая малая доза не является абсолютно безопасной. Поэтому основные дозовые пределы ПДД и ПД должны быть такими, чтобы исключить возможность радиационных поражений человека, а риск появления отдаленных неблагоприятных последствий облучения человека сделать достаточно малым и социально оправданным пользой, которую человечество получает от использования атомной энергии.

Значение ПДД - 5 бэр выбрано таким, что опасность облучения такой дозой за год человека, работающего в условиях воздействия ионизирующих излучений, не превосходило той опасности, которой подвергается человек в других отраслях промышленности, где гарантирована высокая степень безопасности, т. е. риск пострадать на работе мал. Мировой опыт применения указанного ПДД подтверждает сказанное.

В таблице 1.2 в качестве примера приведены значения эквивалентных доз для некоторых распространенных условий облучения по данным ИАЭ им. И. В. Курчатова.

Таблица 1.2

Эквивалентные дозы и соответствующие им

условия облучения

Условия облучения	Эквивалентная доза
1. Просмотр одного хоккейного матча по ТВ	1 мкбэр
2. Ежедневный в течение года 3-часовой просмотр ТВ	0,5 мбэр
3. Перелет самолетом на расстоянии 2400 км	1 мбэр
4. Фоновое облучение за год	100 мбэр
5. Облучение при флюорографии	370 мбэр
6. Допустимое облучение ограниченной части населения за год	500 мбэр
7. Облучение при рентгенографии зубов	3 бэр
8. Допустимое облучение персонала АЭС в нормальных условиях за год	5 бэр
9. Допустимое разовое аварийное облучение населения	10 бэр
10. Допустимое разовое аварийное облучение персонала АЭС	25 бэр
11. Облучение при рентгеноскопии желудка	30 бэр
12. Кратковременное незначительное изменение состава крови	75 бэр
13. Нижний уровень развития легкой степени лучевой болезни	100 бэр

 

Рассмотрим наконец вопрос, связанный с мерой воздействия и.и. или риском. Риск — это вероятность возникновения неблагоприятных последствий для человека (смерть, травматизм, заболевания и т. п.) вследствие облучения, аварии или другой причины, проявление которой носит случайный характер. Например, риск смерти от курения r = 5·10^-4 случаев/(чел∙год). Воздействие облучения на человека связывают с генетическими (наследственными) и соматическими (заболеваниями органов) изменениями. Риск смерти от злокачественных опухолей в результате облучения для 1 человека при эквивалентной дозе 1 Зв составляет r = 1,25·10^-2 1/(чел ∙ Зв), соответственно появление наследственных дефектов – 0,4·10^-2 1/(чел ∙ Зв).

Отметим, что поглощенную эквивалентную дозу, а также характеристики поля иногда называют функционалами поля.

 

Глава 2. ХАРАКТЕРИСТИКИ ИСТОЧНИКОВ

ИЗЛУЧЕНИЯ И ЗАЩИТ

 

Основные понятия и определения

Объект, содержащий радиоактивный материал, или техническое устройство, испускающее или способное в определенных условиях испускать и.и., называется источником ионизирующего излучения. Ядерно-технические установки обычно представляют собой сложные источники излучений. Например, у действующего реактора источником излучения является не только активная зона, но и система охлаждения, оборудование, конструкционные материалы и т. п. Поле излучения реальных сложных источников представляют как суперпозицию полей излучения отдельных более простых источников.

Любой источник излучения характеризуется:

1. Видом излучения,

2. Геометрией источника (размером и формой),

3. Мощностью и ее распределением для протяженных источников,

4. Энергетическим спектром,

5. Угловым распределением излучения.

В соответствии с ГОСТ 8.417-81 (Государственная система обеспечения единства измерений), введем следующие понятия, относящиеся к источникам излучений.

Нуклид — вид атомов с данными числами протонов и нейтронов в ядре.

Радиоактивность — самопроизвольное превращение неустойчивого нуклида в другой нуклид, сопровождающийся испусканием и.и.

Радионуклид — нуклид, обладающий радиоактивностью.

Изотоп — нуклид с числом протонов в ядре, свойственным данному элементу.

Радиоизотоп — изотоп, обладающий радиоактивностью.

Радионуклидный источник и.и. — источник и.и., содержащий радиоактивный материал.

Активность радионуклида. Единицы активности

 

Активность радионуклида в источнике — отношение числа dN радиоактивных распадов (спонтанных ядерных переходов), происходящих в источнике за интервал времени dt, к этому интервалу

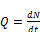(2.1)

Единица активности радионуклида — беккерель (Бк). Беккерель равен активности нуклида в радиоактивном источнике, в котором за время 1 с происходит один радиоактивный распад. Внесистемная единица активности — кюри (Ки). Кюри равна активности нуклида в радиоактивном источнике, в котором за время 1с происходит 3,7 ⋅10¹⁰ Бк.

Отношение активности радионуклида в источнике к массе, объему, площади поверхности (для поверхностных источников) или длине (для линейных источников) источника называется удельной Q_m, объемной Q_v, поверхностной Q_s, или линейной Q_L активностью источника соответственно. Выбор единиц этих величин определяется конкретной задачей. Например, допустимую концентрацию радионуклида в воздухе удобнее выражать в Бк/м³, т. к. суточное потребление человеком воздуха определяется обычно в кубических метрах, соответственно воды в Бк/л.

Распад ядер сопровождается испусканием корпускулярных частиц (частиц с массой отличной от нуля) и (или) фотонов. При этом число радиоактивных распадов далеко не всегда совпадает с числом испускаемых корпускулярных частиц, а также с числом испускаемых фотонов.

Активность характеризует лишь число ядерных переходов. Поэтому также термины, как «альфа- или бета- или гамма- активность», некорректны, следовательно недопустимы. Связь активности радионуклида с числом испускаемых корпускулярных частиц определяется схемой распада нуклида.

 

2.3. Расчет дозных полей от источников гамма- излучения с непрерывным спектром

 

Примером таких источников служат ядерные реакторы, ускорители заряженных частиц (их тормозное излучение). Иногда непрерывным спектром аппроксимируют излучение конструкционных элементов защиты (захватное и активационное излучения), излучение смесей радионуклидов (радиоактивных отходов) и т. д. Об щи м подходом к нахождению дозных полей таких источников является процедура разбиения спектра гамма-излучения на группы. Внутри каждой i-группы энергию гамма-излучения Ε_γί считают постоянной. Мощность дозы P можно представить в виде суммы парциальных P_i, рассчитанных для каждой отдельной группы.

 

(2.2)

где E_y^m — максимальная энергия гамма-квантов в исследуемом спектре; М — число энергетических групп, ΔΕ_γί — ширина энергетического интервала (энергетической группы).

 

Рис.2.1. Зависимость от энергии фотонного излучения поглощенной дозы для единичного флюенса δ_D в ткани (1) и в воздухе (2). ● - эксперимент в тканеэквивалентном фантоме толщиной 30 см.

 

В формуле (2.2) величину δ _Д (E _{γ i})называют удельной поглощенной дозой. Это доза, создаваемая гамма-излучением с энергией Ε_γί и единичным флюенсом F = 1 1/см². На рис. 2.1. приводится график зависимости δ_Д от энергии гамма-излучения в воздухе и ткани.

Если в формулу (2.2) ввести коэффициент качества, получим выражение для мо щн ости эквивалентной дозы

 

, (2.3)

где h (E _{γ i}) — удельная эквивалентная доза, или эквивалентная доза при флюенсе гамма-излучения с энергией E _{γ i} равном единице F = 1 1/см². В приложении, табл. 2, приводятся значения h для гамма-квантов в интервале энергий 5 · 10^-9 - · 10⁴ МэВ.

Глава 3. ЗАЩИТА ОТ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ

 

3.1. Классификация защит

Материалы, используемые для ослабления потоков ионизирующих излучений, располагаемые между источником излучения и защищаемой зоной размещения персонала или оборудования называют защитой.

Защиту от и.и. классифицируют по назначению, типу, компоновке, форме и геометрии. По назначению защиту подразделяют на биологическую, радиационную и тепловую, в соответствии с чем она должна обеспечивать:

— допустимый уровень облучения обслуживающего установку персонала;

— допустимый уровень радиационных повреждений конструкционных и защитных материалов;

— допустимый уровень радиационного энерговыделения и температурного распределения в конструкционных и защитных материалах.

Радиационная и тепловая защиты бывают необходимы лишь на мощных энергетических установках, таких, как ядерный реактор. Защиты делятся на следующие типы:

1. Сплошная защита, целиком окружающая источники излучения. Она может ослаблять излучение одинаково во всех направлениях или быть ослабленной для областей, где допустимый уровень может быть увеличен, например, для областей ограниченного доступа персонала.

2. Раздельная защита, когда наиболее мощные источники и.и. окружает первичная защита, а между первичной и вторичной защитами имеются также источники излучения, например, система теплоносителя (контур многократной принудительной циркуляции (КМПЦ)).

3. Теневая защита устанавливается между источником излучения и защищаемой областью, размеры которой ограничиваются “тенью”, “отбрасываемой” защитой. Особенно часто такая защита используется при ограничениях ее массы и габаритов.

По компоновке различают гомогенную (однородную) и гетерогенную (состоящую из слоев различных материалов) защиты. По форме поверхности наиболее часто на практике встречаются плоская, цилиндрическая и сферическая защиты. Различают защиту также по геометрическому принципу (критерию), выделяя следующие типы: бесконечная, рис.2.2а, полубесконечная с детектором Д на границе среды и источником S в среде, рис. 2.2б и наоборот, рис. 2.2в, барьерная, рис.2.2г, и ограниченная, рис. 2.2д. Все указанные виды защит показаны на рис. 2.2, где источник S и детектор Д предполагаются точечными. Критерий бесконечности защиты, рис. 2.2а, формулируют так: если любое окружение данной защиты дополнительным материалом не изменяет показания детектора Д, защита считается бесконечной.

Полубесконечная среда с детектором на границе среды и источником в среде, рис.2.2б, образуется из бесконечной, рис. 2.2а, если плоскостью АА отсечь заднее по отношению к детектору полупространство. Полубесконечная среда с источником на границе среды и детектором в среде, рис. 2.2в, образуется из бесконечной, рис. 2.2а, если отсечь плоскостью ВВ заднее по отношению к источнику полупространство.

Если одновременно плоскостями АА и ВВ отсечь оба полупространства рис. 2.2а, получится защита барьерной геометрии, рис.2.2г.

Выделение в защите барьерной геометрии лишь части среды, например, параллелепипеда, на противоположных гранях которого находятся источник и детектор, рис. 2.2д, соответствует ограниченной защите. Считается, что среда ограниченная, если ни один из поперечных размеров не может быть принят за бесконечный.

 

 

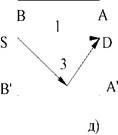Рис. 2.2. Типы защит (по поверхности):

а – бесконечная; б - полубесконечная с детектором Д на границе среды и источником S в среде; в - полубесконечная с источником S на границе среды и детектором Д в среде; г – барьерная; д - ограниченная.

Рассмотрим влияние геометрии защиты, рис. 2.2, на показания детектора. Геометрия защиты при постоянных значениях d и массе вещества защиты между источником и детектором влияет только на рассеянное излучение. В случае бесконечной геометрии, рис. 2.2а, регистрируются рассеянные в области защиты частицы типа 1, 2, 3, а также частицы типа 4, 5 рассеянные в области заднего полупространства защиты по отношения к источнику и детектору. При переходе к другим геометриям регистрируется меньшее число рассеянных частиц. Таким образом, число регистрируемых нерассеянных частиц для всех геометрий, рис. 2.2, постоянно, а число регистрируемых рассеянных частиц для всех геометрий различно. При этом максимальны показания детектора при измерениях в условиях бесконечной геометрии, причем они меньше в полубесконечной среде, еще меньше в барьерной геометрии и минимальны в ограниченной среде. Расчет характеристик поля рассеянного излучения представляет наибольшую трудность при решении задач физики радиационной защиты.

 

3.2. Последовательность проектирования защиты

При расчете радиационной защиты приходится рассматривать вопросы так или иначе связанные с определением полей и.и. или энергии, поглощенной в материалах конструкции, теплоносителе, защите. Глубина проработки и перечень необходимых данных для выполнения расчета зависят от стадии проектирования АЭС.

При расчете защиты на стадии технического проектирования необходимо знать:

· тепловую мощность реактора, кампанию, количество технологических каналов и их размещение в активной зоне;

· размеры активной зоны;

· принципиальную технологическую систему АЭС с перечнем оборудования;

· параметры теплоносителя по участкам технологической схемы: давление, температуру, плотность, паросодержание, скорость и время циркуляции;

· материалы контура, объем теплоносителя, состав примесей;

· состав газов, используемых для технологических нужд;

· возможные аварийные ситуации, связанные с утечкой из контуров теплоносителя, газа, их параметры;

· способ и частоту перезагрузки технологических каналов, количество одновременно перегружаемых каналов, время их хранения на АЭС.

Этот не полный перечень необходимых данных свидетельствует о том большом объеме расчетных и конструкторских работ, который выполняется при проектировании защиты АЭС. Обычно вопросы проектирования решаются в следующей последовательности.

1. Расчет полей нейтронов и гамма-квантов с поверхности активной зоны, расчет плотности потоков нейтронов и гамма-квантов на корпус реактора.

2. Расчет тепловой защиты реактора, энерговыделения в отражателе, тепловых экранах, корпусе реактора.

3. Выбор материалов и расчет защиты от излучения из реактора и ближайших слоев защиты в различных направлениях.

4. Расчет активности теплоносителя и примесей при нормальной работе реактора, а также при нарушении герметичности оболочек тепловыделяющих элементов (твэлов).

5. Определение радиационной обстановки в технологических помещениях АЭС, выбор материалов защиты, толщины стен помещений с оборудованием контуров.

6. Расчет прохождения излучения через неоднородности в защите и разработка специальных мер, снижающих их влияние на радиационную обстановку.

7. Расчет удельной активности газов и выбросов в вентиляционную систему при нормальной и аварийной работе АЭС.

Следует отметить, что в настоящее время для расчета защиты АЭС разработаны соответствующие методики и алгоритмы, реализованные в программах на электронно­вычислительных машинах (ЭВМ). Как правило, решается уравнение переноса излучения (кинетическое уравнение Больцмана) численными детерминистическими (многогрупповыми) или вероятностными (метод Монте-Карло) методами.

Отличительным признаком этих методов является отыскание дифференциальной плотности частиц Ф(r,Е,Ω) в защите, как функции шести переменных, и конструирование с помощью этой функции искомых функционалов (характеристик дозного поля). Решение уравнения переноса требует значительных затрат машинного времени и ЭВМ с большой памятью. Кроме того, алгоритм решения этих задач разработан лишь для геометрически правильных источников и.и. и защит, а также для фиксированного набора характеристик источника. Реальные защиты обычно без существенных отступлений не удается подвести под ограничение той или иной программы и при переходе от решения идеализированной задачи к реальной возникают погрешности, иногда сводящие на нет все преимущества точного метода.

Поэтому методы точного решения кинетического уравнения переноса при разработке защиты АЭС в настоящее время находят двоякое применение: как контрольные тесты при разработке упрощенных методов решения уравнения переноса (теоретический эксперимент) и при решении некоторых частных задач проектирования, требующих большой точности и максимального подпадающих под ограничения программ.

Другой подход к расчету защит от и.и. — использование инженерных и эмпирических методов. Отличительной их особенностью можно считать то, что с их помощью рассчитывают лишь дифференциальный энергетический спектр плотности потока частиц Ф₀(r,Ε),

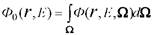
. (3.1)

 

Эти методы расчета не позволяют получить дифференциальное угловое распределение Ф(r,Ε,Ω) или оценивают его очень приближенно. Потребность машинного времени у этих методов значительно меньше и они вполне пригодны для вариантных расчетов при проектировании защиты АЭС.

Эмпирические методы расчета выполняются, как правило, вручную. К ним относятся такие методы, как метод сечения выведения, учет рассеянного излучения с помощью факторов накопления, метод конкурирующих линий и др. Несмотря на кажущуюся простоту эмпирических методов, их использование требует понимания сущности протекающих процессов и четкого знания пределов применимости каждого метода.

Зависимость основных функционалов от толщины защиты имеет экспоненциальный характер, поэтому при правильном использовании эмпирических методов возможны расхождения с точным решением в десятки и сотни раз.

Кинетическое уравнение переноса инвариантно по отношению к нейтронному и гамма-излучению и может быть сформулировано для «частиц», испытывающих те или иные взаимодействия. Однако большинство существующих методов решения кинетического уравнения развиты применительно к одному из этих видов излучения. Это вызвано различием в законах рассеянных нейтронов и гамма-квантов, а также резонансным характером зависимости сечений нейтронов от энергии. По этой причине дальнейшее изложение методов расчета проводится раздельно для нейтронов и гамма-квантов.

3.3. Инженерные методы расчета защиты от гамма-излучения

В настоящем разделе приведены практические методы расчета защиты, относящиеся в основном к точечным изотропным источникам. Однако многие закономерности остаются справедливыми и для протяженных источников.

3.3.1 «Защита» без применения экранов

Для точечных изотропных источников фотонного излучения в непоглощающей среде (когда отсутствует защита) для основных функционалов — мощности дозы Ĥ, Зв/с, и эквивалентной дозы H, Зв, можно написать

^, (3.2)

где Q — активность, Бк; r — расстояние, м; t — время работы в поле излучения источника, с; a = 1,09 Зв/Гр — переходный коэффициент от мощности кермы в воздухе к мощности эквивалентной дозы; Г * — в (Гр·м²)/(с·Бк). Этот способ условно называют «защита временем – количеством – расстоянием», так как при заданных значениях нормативных функционалов и можно рассчитать время работы t, расстояния r, активность Q источника, при которых обеспечивается безопасность без применения экранов.

 

3.3.2. Универсальные таблицы для расчета защиты.

Универсальные таблицы рассчитаны для определения дозовых характеристик от точечных изотропных источников в бесконечной геометрии защиты. Для определения обходимой толщины защиты находят кратность ослабления K — отношение мощности дозы без защитного экрана к мощности дозы в том же месте с экраном:

. (3.3)

Ḣ₀ — находят по формуле (4.2), а Ḣ_d исходя из условий задачи или используя данные НРБ - 99 о допустимых уровнях облучения. Пример таких таблиц приведен в Приложении 1.

Для определения толщины защиты в барьерной геометрии по универсальным таблицам при μ_d ≥ 2 надо требуемую для барьерной геометрии кратность ослабления излучения K_бар умножить на δ - поправку на барьерность, которую можно найти в справочной литературе, и затем для K = K_бар·δ определить толщину защиты по универсальным таблицам. Учет барьерности существенен в области небольших энергий фотонов источника и низкоатомных материалов защиты.

С помощью универсальных таблиц можно решать широкий круг задач, в том числе определять: искомую толщину зашиты (или её избыток) к уже существующей толщине; кратность ослабления по заданной толщине защиты, линейные или массовые эквиваленты отдельных защитных материалов; слои половинного или десятикратного ослабления излучения. С хорошим приближением эти таблицы можно применять для оценки защиты от протяженных источников.

Толщину защитного экрана, снижающую уровни излучения в 2 раза, называют слоем половинного ослабления Δ_1/2. Допустим, что требуется рассчитать защиту для достижения кратности ослабления К в широком пучке, т.е. с учетом рассеянного излучения. Тогда можно записать

К = 2ⁿ, (3.4)

где n — требуемое число слоёв половинного ослабления. Искомая толщина защиты определена из соотношения

d = n·Δ_1/2, (3.5)

если известна толщина слоя половинного ослабления Δ_1/2 материала защиты для условий поставленной задачи.

 

3.3.3. Метод конкурирующих линий

Пусть имеется немоноэнергетический излучатель с дискретным набором из разных энергий E₁, Е₂,...E_j,...Е_m и соответствующим процентным вкладом в мощность эквивалентной дозы n₁,..., n_m для каждой энергии с учетом её относительного вклада в мощность эквивалентной дозы с помощью рассмотренных выше методов или иных методов определяют необходимую толщину защиты. Таким образом, получают набор значений толщин d₁, d₂,...d_j,...d_m.

Назовём условно главной линией спектра ту, для которой требуется наибольшая толщина защиты, и обозначим её d_гл. Линию спектра, который требует меньшей (последующей после главной) толщины, назовём конкурирующей, а соответствующую ей толщину защиты обозначим d_k. Пусть Δ_1/2. — слой половинного ослабления. Тогда толщина защиты с хорошим приближением может быть определена из соотношений:

если (d_гл – d_к) = 0,то d = d_гл + Δ_1/2,

если, 0 < (d_гл – d_к) < Δ_1/2 то d = d_гл + Δ_1/2(4.6)

если (d_гл – d_к) > Δ_1/2, то d = d_m.

Поскольку Δ_1/2 зависит не только от энергии, но и от кратности ослабления (сл. и от толщины защиты), его определяют в области данных значений толщины d_гл и d_K. При этом выбирают ту энергию, которая дает наибольшее значение Δ_1/2. Этот прием называют методом конкурирующих линий, потому, что по мере увеличения абсолютной толщины защиты главная и конкурирующая линия могут меняться местами, или уступать место третьей линии, которая при меньших кратностях ослабления была второстепенной.

Для непрерывных энергетических спектров применяют процедуру разбиения их на энергетические интервалы и определения в каждом из них эффективной дискретной энергии E_t. Обычно ограничиваются тремя или четырьмя группами. Важно, чтобы внутри интервала энергии были объединены с наибольшим различием коэффициента ослабления. В этих задачах удобно располагать Ei в порядке уменьшения энергии, т.е. Ει > Ε₂ > Ε₃ >... > Ε_]· >... > Ε_Μ и, следовательно, в порядке уменьшения проникающей способности (если E_i < Е_мин).

Метод конкурирующих линий широко используется при проектировании защиты от гамма-излучения смеси продуктов деления.

 

3.3.4. Закон ослабления плотности потока

гамма- излучения веществом.

Пусть моноэнергетический источник гамма- излучения (точечные или плоско-параллельные) создают в точке наблюдения А в отсутствии защиты плотности потока гамма-квантов Ф₀ (с энергией E_y). Если между источником и точкой А поместить защиту толщиной d из вещества, имеющего для гамма-квантов источника, т. е. для гамма-квантов с энергией Ε_γ линейный коэффициент ослабления плотности потока μ, то в тонком слое dx на глубине x будет поглощено

dФ = -μ· Ф · dx (3.6)

гамма-квантов.

Разделяя переменные и интегрируя это уравнение, получаем выражение

ФА = Ф ₀ exp(−μ ⋅ d), (3.7)

Поскольку, по формуле P = I ⋅μ em = Ф ⋅ E ⋅μ em, то выражение (3.7) можно записать и для мощности дозы

P_A = P ₀ ⋅ exp(−μ ⋅ d). (3.8)

Соотношения (3.7) и (3.8) называют законами ослабления плотности потока и мощности дозы гамма-излучения в условиях хорошей геометрии (узкого пучка). Понятие хорошей геометрии предполагает, что в точке А нас интересует гамма- излучение, которое прошло через защиту без взаимодействия, т.е. не изменяя свою энергию.

В общем случае в точку наблюдения А кроме гамма-квантов с энергией E_γ могут попасть гамма- кванты с другими энергиями E`_γ < E_γ, т.е. рассеянные, обязанные своим появлением комптоновскому рассеянию гамма-квантов источника в защите.

Геометрию, при которой детектор регистрирует нерассеянное и рассеянное первичное и вторичное излучение, называют геометрией широкого пучка (плохой геометрией). Рассеянное в среде излучение источника учитывают введением в закон ослабления узкого пучка (3.7) и (3.8) сомножителя — фактора накопления фотонного излучения.

Закон ослабления плотности потока (и других функционалов поля) гамма-излучения в защите с учетом рассеянного в защите оказалось возможным записать в удобном для практического использования виде

Ф_А =Ф₀ ⋅ exp(−μ ⋅ d) ⋅ BЧ (μ ⋅ d), (3.9)

или, для мощности дозы гамма-излучения

P_А = P₀ ⋅ exp(−μ ⋅ d) ⋅ BД (μ ⋅ d). (3.10)

Соотношения (3.9) и (3.10) — это общие законы ослабления плотности потока и мощности дозы гамма-излучения, или законы ослабления в условиях широкого пучка (или в условиях «плохой» геометрии). Отметим, что В_Ч (μ· d) и Вд (μ· d) называют числовым и, соответственно, дозовым факторами накопления рассеянного гамма-излучения при толщине защиты μd, измеренной в длинах свободного пробега. Длина свободного пробега гамма-квантов в защите равна 1/μ. Очевидно, что

(3.11)

Соответственно

(3.12)

 

где Ф'_А и P'_А — компоненты плотности потока и мощности дозы рассеянного гамма-излучения в точке А.

Фактор накопления рассеянного излучения зависит от энергии гамма-излучения, свойств материала защиты (Z), её толщины и геометрии: B = B(E,Z,μd). Из формул (3.11) и (3.12) следует, что фактор накопления равен кратности превышения характеристик поля нерассеянного и рассеянного первичного и вторичного излучения над характеристиками поля нерассеянного первичного излучения, т. е. характеризует отношение показания детектора при измерении в геометрии узкого пучка. Иногда рассматривают факторы накопления поглощенной энергии (для расчета тепловыделения в защите В_П (μ · d), кермы В_К (μ · d) и др.)

 

3.3.5. Факторы накопления рассеянного гамма- излучения.

Фактор накопления зависит от условий задачи: регистрируемого эффекта, характеристик источника (энергетического состава, геометрии и углового распределения излучения), свойств защитной среды, взаимного расположения источника, защиты и детектора. По регистрируемым эффектам выделяют следующие факторы накопления (для моноэнегретических источников фотонов с энергией Е_у): числовой

, (3.13)

дозовый (для поглощенной дозы в воздухе)

(3.14)

поглощенной энергии (для поглощенной в среде энергии)

(3.15)

кермы

’ (3.16)

и энергетический (для плотности потока энергии фотонов)

^, (3.17)

где Φ(μ · d, E) — пространсвенно-энергетическое распределение плотности потока нерассеянного и рассеянного первичного и вторичного излучения, Φ₀(μ·d) — пространственное распределение плотности потока нерассеянного в среде первичного излучения, μ_em^B (E γ), μ_em^ср — коэффициенты поглощения энергии фотонов в воздухе и некоторой среде соответственно, μ_km^ср — коэффициент передачи энергии E фотонов в некоторой среде.

Энергетический фактор накопления всегда меньше числового, так как энергия рассеянных фотонов E в числителе (3.17) всегда меньше Eγ в числителе этой же формулы.

В формулах (3.13) - (3.17) μd — это толщина, материала защиты. Значения величин факторов накопления для различных материалов защиты приводятся в справочной литературе.

С увеличением толщины среды между источником и детектором факторы накопления возрастают. Это связано с накоплением числа рассеянных фотонов по мере удаления от источника. На малых расстояниях от источника — это фотоны, испытавшие много рассеяний на малые углы.

Для высоких энергий излучения источника и элементов с умеренно-низкими Z скорость возрастания фактора накопления близка к линейной. Для тяжелых элементов фактор накопления растёт медленно с расстоянием.

С увеличением Z фактор накопления в большинстве случаев убывает. Отметим, что фактор накопления поглощённой энергии обычно используется при расчёте тепловыделения в защите.

Приведённые на рис. 10 типичные траектории нерассеянных и рассеянных фотонов для разных геометрий защиты позволяет написать следующее соотношение для факторов накопления B_∞>B_1/2 > В_бар > В_огр, где В_∞, В_бар, В_огр факторы накопления соответственно для бесконечной, полубесконечной, барьерной и ограниченной геометрией защиты при постоянной толщине среды между источником и детектором.

Существует несколько способов представления факторов накопления: табличный, графический, а также в виде аналитического представления (в виде суммы двух экспонент). В качестве примера на рис.3.1 даны зависимости дозовых факторов накопления в водной и свинцовой средах.

При расчёте защит от протяжённых источников факторы накопления попадают под знак интеграла. Графическое и табличное представления факторов накопления существенно затрудняет расчёты. Поэтому были предприняты попытки представить информацию о факторах накопления в удобном аналитическом виде — аппроксимировать с помощью экспонент

(3.18)

где коэффициенты A₁, α₁, α₂ зависят только от E_γ и Z материала защиты и не зависит от толщины защиты μd. В справочной литературе даны значения A₁, α₁, α₂ для различных материалов и энергий для точечных изотропных моноэнеогетических источников в условиях бесконечной геометрии. Экспоненциальное представление рассеянного излучения позволяет сохранить общий вид интегралов, выведенных для различных частных случаев распространения первичного излучения источников различных геометрических форм. Таким образом, основное преимущество представления фактора накопления в виде (3.18) состоит в том,

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: