Пример выполнения задания

Дано: крышка ящика ABDE весом G = 240 Н удерживается в открытом положении (угол α = 60°) при помощи стержня ЕК, образующего с горизонталью угол b = 60° (рис. 1.8). Сдвигающая сила Р = 20 Н параллельна оси Ах. Размеры крышки: АВ = 1 м, АЕ = 0,6 м.

Определить реакции в подпятнике А и в подшипнике В, а также усилие в стержне ЕК.

 

Рис. 1.8.

Решение

Выделим объект равновесия – крышку ящика ABDE. Рассматриваем равновесие внешних сил, приложенных к объекту равновесия. Крышка имеет две закрепленные точки: подпятник А и подшипник В. Для упрощения уравнений равновесия начало координат помещаем в одну из этих точек А и ось х проводим через обе точки (рис. 1.9).

Представим крышку как свободное тело, мысленно удалив наложенные связи. Взамен отброшенных связей прикладываем реакции этих связей. Реакция стержня S_E направлена вдоль стержня. Подшипник В схематически представляет собой кольцо, сквозь которое проходит ось, скрепленная с крышкой. Подшипник не ограничивает перемещение крышки вдоль оси х, а препятствует перемещению в плоскости, перпендикулярной этой оси. Разложим полную реакцию подшипника на составляющие Y_B и Z_B, направив их параллельно осям у и z.

Подпятник А схематически представляет собой совокупность такого же кольца и опорной плоскости. Благодаря наличию кольца реакция подпятника имеет составляющие Y_А и Z_А, а опорная плоскость дает составляющую Х_{А .} Направим и эти силы вдоль соответствующих осей координат.

Приложим к объекту равновесия внешнюю активную (задаваемую) нагрузку, в соответствии с условием задачи, т.е. сосредоточенную силу Р и вес крышки G – в точке пересечения диагоналей прямоугольника ABDE, считая крышку однородной).

 

Рис. 1.9.

 

Шесть неизвестных сил – реакций связей Х_А, Y_А, Z_А, Y_B, Z_B, S_E могут быть определены из шести уравнений равновесия:

;

;

;

;

;

При составлении уравнений моментов следует учитывать, что если линия действия силы параллельна оси или пересекает ее, то момент этой силы относительно оси равен нулю.

Чтобы облегчить вычисление моментов сил относительно осей координат и проекции сил на оси координат, проецируем систему сил на три координатные плоскости, каждая из которых перпендикулярна одной из координатных осей (рис. 1.10.- 1.12.).

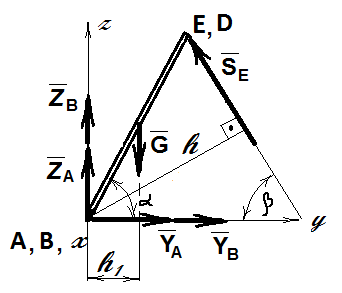
Рис. 1.10

 

Рис. 1.11.

Составим уравнения проекций сил на оси z и y, а также уравнение моментов относительно оси Ах, используя рис. 1.10:

åF^E_iу = Y_A + Y_В - S_E× cos b = 0; (1.1)

åF^E_iz = Z_A + Z_B + S_E × sin b - G = 0; (1.2)

åМ^Е_iAx = S_E×h - G h₁= 0, (1.3)

где h – плечо проекции силы S_E на плоскость Аyz относительно точки А, вычисляется по формуле: h = AE× sin 60° = 0,52 м; h₁ = (AE/2)×cosa.

 

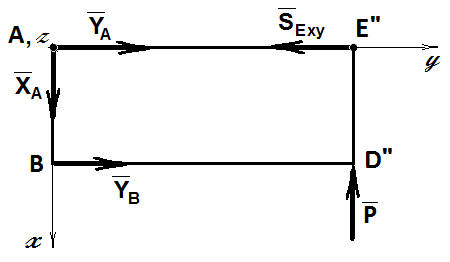
Рис. 1.12.

 

После подстановки численных значений уравнения (1.1) - (1.3) получают вид:

Y_A + Y_В - S_E× 0,5 = 0; (1.4)

Z_A + Z_B + S_E × 0,87 - 240 = 0; (1.5)

S_E×0,52 - 36 = 0, (1.6)

 

Система трех алгебраических уравнений (1.4) - (1.6) содержит пять неизвестных, из которых пока может быть найдено только одно.

S_E = 36/0,52 = 69,23 Н.

 

Составим уравнения проекций сил на ось х и моментов относительно оси Ау, используя рис. 1.11. Отметим, что на рис 1.11 проекция силы S_E на плоскость Аxz определяем по формуле: S_Ezx = S_E×sin b, а расстояние. АЕ' = AE×sina = 0,6×sin60° = 0,52 м

å F^E_iх = X_A - P = 0; (1.7)

å М^Е_iAy = G×AB/2 - P×. АЕ' - Z_B×AB = 0,(1.8)

После подстановки численных значений уравнения (1.7) - (1.8) получают вид:

X_A - 20 = 0; (1.9)

120 - 10,4 - Z_B= 0, (1.10)

 

решая уравнения находим X_A = 20 Н и Z_B= 109,6 Н.

Составим уравнения моментов относительно оси Аz, используя рис.1.12. Отметим, что на рис.1.12 проекция силы S_E на плоскость Аxy определяется выражением: S_Exy = S_E×cos b, а расстояние АЕ''= AE×cosa = 0,6×cos60° = 0,3 м.

å М^Е_iAz = P× АЕ'' + Y_B×AB = 0, (1.11)

После подстановки численных значений уравнение (1.11) принимает вид:

6 + Y_B = 0, (1.12)

Откуда Y_B = -6 Н.

Подставляя в уравнения (1.1) - (1.2) значения Y_B = -6 Н, S_E = 69,23 Н

и Z_B= 109,6 Н, определяем Y_A и Z_A.

Y_A - 6 - 69,23 × cos 60° = 0; (1.13)

Z_A +109,6 + 69,23 × sin 60° - 240 = 0, (1.14)

 

из которых находим Y_A = 40,62 Н и Z_A= 70,42 Н.

 

Найденные реакции связей:

X_A = 20 Н, Y_A = 40,62 Н, Z_A = 70,42 Н.

Y_B = -6 Н, Z_B = 109,6 Н.

S_E = 69,23 Н.

R_A = H

R_B = H

Значение реакции связи Y_В оказалось отрицательным, следовательно, ее действительное направление противоположно показанному на рис. 1.9, 1.10 и 1.12.

2. Методические рекомендации
к защите задания

Перед выполнением задания на тему «Статика в пространстве» необходимо изучить соответствующий материал по учебнику, конспекту лекций и записям, сделанным на практических занятиях, а также выяснить на консультации вопросы, вызывающие затруднения.

Задание следует выполнять на листах, скрепленных в брошюру.

Образец титульного листа приведен в приложении.

Содержание работы, предъявляемой к проверке. Решение задачи следует начинать с условия: рисунка – схемы механической системы заданной по условию задания; записать, что дано и что требуется найти. Решение должно содержать рисунок – расчетные схемы с указанием размеров и всех векторов, заданных в условии задания и определяемых решением; метод – каким образом составлены уравнения; уравнения в общем виде; уравнения с численными значениями; значения вычисленных характеристик с указанием единиц измерения. (Допускается составить подробные уравнения равновесия, в которых неизвестные – только реакции связей, и не решать их). Решение может содержать краткие пояснения. Выполненное задание следует сдать на проверку преподавателю. Задание можно защищать после исправления ошибок, отмеченных преподавателем. Для успешной защиты необходимо знать и понимать решение задания. Также перед защитой задания в качестве подготовки к защите рекомендуется ответить на следующие вопросы:

1. Что называют моментом силы относительно точки (применительно к «пространственной задаче»)?

2. Чему равен модуль момента силы относительно точки?

3. Как выразить момент силы относительно точки в виде векторного произведения?

4. Момент силы относительно точки есть вектор – связанный, скользящий, свободный?

5. Что называют моментом силы относительно оси?

6. Когда момент силы относительно оси равен нулю?

7. При каком направлении силы, приложенной к данной точке, ее момент относительно данной оси наибольший?

8. Как назначают знак момента силы относительно оси?

9. Какая зависимость связывает величины – момент силы относительно точки и момент силы относительно оси, проходящей через эту точку?

10. Как изобразить момент пары сил вектором?

11. Чему равен модуль момента пары сил?

12. Как назначают знак момента пары сил?

13. Можно ли выразить момент пары сил в виде векторного произведения?

14. Момент пары сил есть вектор – связанный, скользящий, свободный?

15. Существует ли в плоскости действия пары точка, относительно которой момент этой пары сил равен нулю?

16. Чему равен момент пары сил относительно любой точки в пространстве?

17. Как производят сложение пар сил в пространстве?

18. Основные виды пространственных связей – каковы их названия и какого типа реакции им соответствуют?

19. Что называют главным вектором системы сил?

20. Что называют главным моментом системы сил?

21. Зависит ли главный вектор системы сил от выбора центра приведения?

22. Зависит ли главный момент системы сил от выбора центра приведения?

23. Сколько независимых уравнений равновесия, какие именно, можно составить для твердого тела, находящегося в равновесии под действием пространственной произвольной системы сил?

24. Сколько независимых уравнений равновесия и какие уравнения можно составить для твердого тела, пребывающего в равновесии под действием пространственной системы параллельных сил?

25. Сколько независимых уравнений равновесия и какие уравнения можно составить для твердого тела, пребывающего в равновесии под действием пространственной системы сходящихся в точке сил?

26. Чему равен главный вектор системы пар сил, действующих на твердое тело?

27.Как формулируются условия равновесия твердого тела, при действии на него системы пар сил?

 

 

3. Варианты расчетных схем
и условия заданий

 

Вариант № 1

Тетраэдр закреплен петлей (цилиндрическим шарниром) А, сферическим шарниром В и свободно опирается вершиной С на каток. Определить реакции опор, вызванные действием силы F, приложенной в вершине тетраэдра, действующей в плоскости Q параллельной плоскости (xy). у₁ || y. Точки А, В, С лежат в плоскости (xy).

 

Номер варианта	F, кH	α, град

Вариант № 2

Изогнутый под прямым углом стержень ABDC находится в горизонтальной плоскости. Стержень закреплен подпятником А и подшипником В. В плоскости диска по касательной действует сила S под углом γ к вертикали. В точке С стержня приложена сила Р под углом α к вертикали и углом β линии СК находящейся в горизонтальной плоскости. Определить реакции опор и силу S, необходимую для равновесия.

 

 

 

Номер варианта	P, H	l1, м	l2, м	l3, м	l4, м	α, град	β, град	γ, град	R, м
		1,0	1,0	1,0	1,0				0,5
		2,0	1,0	0,5	1,5				0,1
		3,0	1,5	1,0	2,0				0,8
		1,5	1,5	2,0	1,0				1,0
		1,5	1,5	1,5	1,5				2,0
		2,0	2,0	1,0	1,5				1,0
		1,0	1,5	1,5	2,0				1,0
		2,5	2,0	3,0	1,0				0,5

 

Вариант № 3

К балке АВ, один конец которой заделан, в точке В приложена сила Р, лежащая в горизонтальной плоскости. В сечении С под прямым углом жестко прикреплена балка CD. В концевом сечении балки CD действует пара сил с моментом M=P∙ l. Плоскость действия пары сил расположена под углом β отсчитываемым от горизонтальной плоскости. Определить реакции заделки.

 

 

Номер варианта	P,H	l,·м	α, град	β, град
		2,5
		0,5

Вариант № 4

На руль шлюпки при ее повороте действует сила давления воды Q, направленная перпендикулярно к плоскости пера руля. Вес руля Р. Определить в условиях равновесия реакции опор А, B, а также величину силы S, приложенной к румпелю DE. Сила S расположена в горизонтальной плоскости.

 

 

 

Номер варианта	Q, H	P, H	β, град	AK, м	AB, м	BE, м	DE, м	CK, м	OC, м
				0,4	0,60	0,20	0,56	0,14	0,25
				0,3	0,55	0,30	0,66	0,22	0,34
				0,35	0,75	0,25	0,50	0,25	0,19
				0,45	0,49	0,35	0,58	0,29	0,1
				0,50	0,51	0,29	0,64	0,31	0,21
				0,33	0,55	0,36	0,69	0,33	0,25
				0,42	0,58	0,23	0,54	0,19	0,09
				0,39	0,45	0,33	0,51	0,23	0,11

 

 

 

Вариант № 5

Грузоподъемный механизм находится в равновесии под действием груза Q, реакций внешних связей. Найти реакции шарниров А, В, натяжение удерживающих тросов КЕ, DS. Высота (K Kxy) = h. Установка симметрична относительно плоскости yz. VA=a-b. Углы α, β, δ определены в вертикальных плоскостях, угол γ – в горизонтальной.

 

 

 

Номер варианта	Q, кH	β, град	γ, град	a, м	b, м	h, м	R, м	α, град	AE, м	АК, м	δ, град
1,0						0,79	0,1		1,0	0,87
1,2						2,05	0,2		1,5	2,15
1,1						0,99	0,3		1,3	1,09
1,3						0,87	0,2		1,2	0,94
1,0						1,43	0,4		1,1	1,48
0,9						1,12	0,3		1,4	1,31
1,1						1,28	0,1		0,9	1,35
						0,99	0,2		1,3	1,09

 

 

Вариант № 6

Вертикальная мачта АV весом Р закреплена в подпятнике А и подшипнике В. В точке О мачты закреплены тросы OK, OD,OE, натяжения, которых F_OK, F_OD, F_OE, известны. Определить опорные реакции, если OV=0,25AO.

Мачту АV считать однородным стержнем.

 

 

Номер варианта	Р, кH	FOK, H	FOD, H	FOE, H	АВ, м	АО, м	α, град	β, град	γ, град
	1,2				0,8	4,0
	1,0				0,7	4,5
	1,4				0,9	3,0
	1,3				0,5	5,0
	1,1				0,8	3,5
	1,5				0,6	4,6
	1,2				0,9	4,5
	1,6				0,7	6,0

 

 

 

Вариант № 7

Вал цилиндрического редуктора, несущий косозубое колесо 1 и прямозубую шестерню 2 установлен в подшипнике А и подпятнике В. Определить из условия равновесия вала окружное усилие на колесе Р₁ и реакции опор, если d₁=0,25 м, l₁=0,2 м, Т₂=0,3Р₂, Т₁=0,25Р₁. (х₂||х₃||x, диаметры колес d₁, d₂). Точки приложения усилий в зубчатых зацеплениях расположены на вертикальных диаметрах зубчатых колес.

 

 

Номер варианта	P 2, кH	Q1/P1	d2 /d1	l2 /l3	l1 /l3
	1,5	0,14	0,8	0,8	1,1
	2,5	0,13	1,2	0,7	1,2
	3,5	0,12	0,5	0,6	1,1
	4,5	0,14	0,8	0,6	1,2
	4,5	0,15	1,2	1,2	1,1
	3,5	0,12	1,2	1,3	1,2
	2,5	0,15	0,8	1,2	1,2
	5,5	0,13	1,2	1,2	1,2

 

 

Вариант № 8

Коленчатый стержень АDEK установлен в горизонтальной плоскости, нагружен горизонтальной силой Р и силой Q, образующей с вертикальной плоскостью угол α. Весом стержня пренебречь. Определить реакции подшипников A, B, H.

 

 

 

Номер варианта	P, H	Q, H	AD, м	DB, cм	ED, cм	EK, cм	EH, cм	α, град	β, град

 

 

Вариант № 9

Коленчатый стержень AHDE весом Р находится в равновесии. Плоскость действия пары сил с моментом М параллельна плоскости (xy), ОО₁ || x. Определить реакции связей: сферического шарнира А, цилиндрического шарнира В, каната КЕ.

 

Номер варианта	P, H	M, H·м	AH, м	BH, м	HD, м	DE, м	α, град	β, град
			0,4	0,2	0,6	0,4
			0,5	0,3	0,4	0,5
			0,3	0,25	0,5	0,3
			0,6	0,35	0,7	0,35
			0,5	0,2	0,75	0,5
			0,4	0,4	0,8	0,25
			0,5	0,35	0,85	0,3
			0,8	0,3	0,6	0,4

 

 

Вариант № 10

Однородная балка весом Р укреплена шарнирно в точке А и удерживается в горизонтальном положении двумя тросами BD и DE, составляющими с горизонтом углы β₁, β₂. В точке К к балке подвешен груз Q. Определить реакции шарнира Аи натяжения тросов.

 

 

 

Номер варианта	P, кH	Q, кH	AO, м	OK,·м	AD, м	α1, град	β1, град	α2, град	β2, град
				1,5

 

 

Вариант № 11

Однородная треугольная плита АВК весом Р прикреплена шарнирно вершиной А к неподвижному основанию и удерживается в горизонтальном положении при помощи невесомых стержней BD, BE, KE. EO=AD=AO=AB. Угол α определен в плоскости, параллельной плоскости (xz). Определить реакции шарнира А и стержней.

 

 

 

Номер варианта	P, H	F, H	α, град
			-45
			-60

 

Вариант № 12

Два одинаковых однородных стержня AK и BK весом P каждый соединены жестко между собой и прикреплены петлей А и неподвижным шарниром B. Невесомый стержень DE образует с вертикальной плоскостью угол α и удерживает механическую систему AKB в горизонтальном положении. AD=DK. ﮮδ=45^º Определить реакции опор А, B и усилие в стержне DE.

 

 

Номер варианта	P, H	AB, м	α, град	β, град
		0,45
		0,34
		0,52
		0,64
		0,48
		0,36
		0,24
		0,43

 

Вариант № 13

Момент М, вращающий ротор, уравновешен окружным усилием Р в зубчатой конической передаче и реакциями опор А и D. Усилие Р перпендикулярно оси x₁ (x₁ ║ x, y₁ ║ y), составляет с осью у₁ угол α и приложено в точке, лежащей на окружности радиуса R. Вес вертикального ротора с зубчатым колесом радиуса R равен Q. Определить реакции подшипника А, подпятника D и усилие Р.

 

Номер варианта	Q, кH	R, м	α, град	M, кН·м	a, м	b, м
		0,5			0,7	1,0
		0,2			0,3	0,8
		0,3			0,4	0,5
		0,4			0,6	1,2
		0,8			0,8	1,3
		0,3			0,7	1,1
		0,5			0,8	1,5
		0,7			0,9	1,7

Вариант № 14

На валу червяка D радиуса r_D насажен шкив K радиуса r_K ременной передачи. Определить, исходя из равновесия вала, натяжения S₁ и S₂ ветвей ремня, реакции радиально-упорного (подпятника) А и радиального В подшипников вала при известных соотношениях: Т/Р=1,25; Q/P=4; S₁/S₂=2. Силы, действующие в червячном зацеплении, приложены в точке, лежащей на окружности радиуса r_D.

 

 

Номер варианта	P, кH	rD, мм	rK, мм	l1, мм	l2 / l1	l3 / l1	α, град	β, град
	3,5				1,1	0,7
	4,0				0,9	0,8
	4,5				1,1	0,6
	5,0				0,9	0,7
	5,5				1,1	0,8
	5,0				0,9	0,6
	4,5				1,1	0,7
	4,0				0,9	0,8

 

Вариант № 15

Найти реакции протяженного шарнира А, усилие пружины ВК (приложено в точке В, направленно к точке К) в случае равновесия механической системы. Натяжения S₁ и S₂ в ветвях ременной передачи равны. (КB || Ax, углы α и γ отсчитаны от прямых, параллельных оси Ax). Вес шкива D (G_D) считать приложенным в точке С, а силы натяжения – приложенными к точкам находящимися на окружности радиуса R_D. (В реакциях шарнира А следует учитывать кроме ограничений накладываемых обычным неподвижным шарниром, препятствие защемлениям при поворотах вокруг осей x и z).

 

 

Номер варианта	S1, кH	GD,, кH	l 1, м	l 2, м	l 3, м	h, м	RD, м	α, град	β, град	γ, град
			0,5	0,7	1,0	0,2	0,3
			0,4	0,6	0,9	0,3	0,2
			0,6	0,9	1,2	0,5	0,4
			0,3	0,7	0,8	0,4	0,3
			0,4	0,5	0,7	0,6	0,4
			0,7	1,1	1,1	0,5	0,5
			0,8	1,2	1,3	0,4	0,7
			0,2	0,4	0,9	0,7	0,6

Вариант № 16

Стержневая конструкция жестко заделана в точке О. AD=0.75∙DE; AD= l/3;AB=AO=l_{1 .} Определить реакции в точке O.

 

 

 

 

Номер варианта	F1, H	F2, H	q, H/м	q0, H/м	l, м	l1, м
						1.5

 

 

Вариант № 17

Криволинейный стержень жестко заделан в точке О. OB=BC=l; AB=2l; AD=1,6l; DE=1,2l. Определить реакции заделки.

 

Номер варианта	P1, кH	q, кH/м	P 2, кH	M, кН·м	l, м	α, град

 

 

 

Вариант № 18

Откидной трап весом Р, длиной l прикреплен к борту цилиндрическими шарнирами А, В и стержнем КЕ. Трап с вертикальной плоскостью образует угол α. На середине нижней ступени стоит человек весом Q. Определить реакции шарниров А, B и стержня КЕ (весом стержня пренебречь).

 

 

 

Номер варианта	P, H	Q, H	α, град	BH, ·м	EH, м	AB, м	BK, м
					0,5 l	0,5 l	0,5 l
					0,5 l	0,6 l	0,8 l
					0,3 l	0,5 l	0,4 l
					0,4 l	0,3 l	0,6 l
					0,5 l	0,4 l	0,7 l
					0,4 l	0,5 l	0,8 l
					0,2 l	0,6 l	0,5 l
					0,3 l	0,3 l	0,4 l

 

Вариант № 19

Однородная пластина весом Р, имеющая форму равностороннего треугольника, закреплена петлями А и В (АВ || x, AB=a). Вершина D опирается на гладкую вертикальную стену. Плоскость пластины составляет с горизонтальной плоскостью угол α. Центр тяжести пластины находится в точке пересечения медиан. Определить реакции петель и стены.

 

 

 

Номер варианта	P, кH	a, м	α, град
		1,3
		2,3
		2,5
		1,5
		1,8
		2,3
		2,5
		3,5

 

 

 

 

Вариант № 20

 

Силы F₁ и F₂, действующие на зубчатые колеса вала АВ направлены под углами α и β,соответственно, к горизонтальным касательным x₁ и x₂ и расположены в вертикальной плоскости. Радиусы зубчатых колес R₁ и R₂. Найти реакции подшипников (неподвижных цилиндрических шарниров) А и В.

 

Номер варианта	F1, кH	F2, кH	R 1, м	R 2, м	l 1, м	l 2, м	l 3, м	β, град	α, град
			0,2	0,4	0,2	0,2	0,3
			0,4	0,5	0,4	0,6	0,2
			0,6	0,10	0,2	0,3	0,4
			0,3	0,8	0,3	0,4	0,9
			0,5	0,7	0,5	1,0	0,7
			0,4	0,8	0,6	0,6	0,4
			0,2	0,6	0,4	0,5	0,3
			0,3	0,5	1,2	1,8	0,9

 

 

 

Вариант № 21

Горизонтальная антенна весом Р прикреплена к вертикальной стойке ОК, установленной в подпятнике О и удерживаемой тремя растяжками. AO=l, KC=0,25l, AK=0,1l. Натяжения растяжек AD и AB равны. Точки O, D, B, E лежат в плоскости (xy). Определить реакции связей в точке О и натяжения растяжек.

 

 

 

Номер варианта	P, кH	l, м	α, град	β, град

 

Вариант № 22

Однородная прямоугольная плита весом Q находится в равновесии опираясь на горизонтальную поверхность в точках А и В и образуя с этой поверхностью угол α. Определить реакции опорной поверхности в точках А, B, величины сил F₁ и F₂ натяжение троса в сечении К. Толщиной плиты пренебречь.

 

 

 

Номер в ⇐ Предыдущая12 Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...