Разработка проекта стандарта (окончательная редакция) и представление его для принятия

3.4.1 ТК (ПК) с учетом поступивших отзывов готовит окончательную редакцию проекта стандарта.

3.4.2 Проект стандарта (окончательную редакцию) с пояснительной запиской ТК (ПК) направляет:

- членам ТК (ПК);

- органам государственного контроля и надзора, если они не являются членами ТК (ПК), и если это необходимо;

- в научно-исследовательскую организацию (в двух экземплярах).

Члены ТК (ПК) рассматривают проект стандарта в порядке и в сроки, установленные ТК (ПК).

Органы государственного контроля и надзора, которые не являются членами ТК (ПК), в месячный срок со дня получения проекта стандарта согласовывают этот проект или дают по нему заключение с обоснованными предложениями по требованиям проекта стандарта, относящимсяк их компетенции.

Научно-исследовательская организация готовит заключение на проект стандарта, обеспечивает его издательское редактирование, направляет в ТК (ПК) заключение и экземпляр проекта стандарта, прошедшего издательское редактирование, в срок, не превышающий месяца со дня получения проекта.

3.4.3 ТК (ПК) с учетом предложений членов ТК (ПК), согласования с органами государственного контроля и надзора, заключения научно-исследовательской организации и результатов издательского редактирования дорабатывает проект стандарта.

При наличии разногласий по проекту стандарта ТК (ПК) организует рассмотрение и снятие этих разногласий.

3.4.4 ТК (ПК) на заседании рассматривает проект стандарта и проводит по нему голосование.

Решение заседания оформляют протоколом. В протоколе должны быть указаны результаты голосования каждого предприятия (организации) - члена ТК (ПК).

Допускается подтверждение согласия с проектом стандарта предприятий (организаций) - членов ТК (ПК) письмом, телеграммой, телефаксом, телетайпограммой, подписанной руководителем (заместителем руководителя) предприятия (организации) - члена ТК (ПК), или подписью руководителя (заместителя руководителя) предприятия (организации) на проекте стандарта, если постоянный полномочный представитель предприятия (организации) - члена ТК (ПК) не имел возможности присутствовать на заседании.

При получении согласия всех членов ТК (ПК) с проектом стандарта допускается не проводить заседание ТК (ПК).

Запись «Согласовано с замечаниями» не допускается.

3.4.5 ТК (ПК) одобряет проект стандарта, рекомендует его для принятия Госстандартом России (Госстроем России) и направляет в Госстандарт России (Госстрой России), если с этим проектом согласны не менее двух третей предприятий (организаций) - членов ТК (ПК).

При этом проект стандарта не может быть направлен для принятия в следующих случаях:

- если за него не проголосовали члены ТК (ПК), являющиеся полномочными представителями органов государственного контроля и надзора;

- если его не согласовали органы государственного контроля и надзора, не являющиеся членами ТК (ПК).

3.4.6 ТК направляет для принятия в Госстандарт России (Госстрой России) проект стандарта (окончательную редакцию) в трех экземплярах, один из которых должен быть первым, с сопроводительным письмом, подписанным председателем ТК, и следующей документацией в одном экземпляре:

- пояснительной запиской к проекту стандарта (в соответствии с 3.3.1);

- протоколом заседания ТК (ПК) по рассмотрению окончательной редакции проекта стандарта;

- подлинными документами, подтверждающими согласование окончательной редакции проекта стандарта, если оно проводилось;

- экземпляром проекта стандарта, прошедшего издательское редактирование.

Одновременно проект стандарта (окончательную редакцию) с приложением пояснительной записки и протокола заседания ТК (ПК) или документов, подтверждающих согласование проекта стандарта с членами ТК (ПК), направляют заказчику стандарта.

3.4.7 В случае разработки стандарта вне рамок ТК предприятия, общественные объединения разрабатывают проект стандарта с учетом порядка, предусмотренного подразделами 3.2-3.4.

При наличии ТК по данному объекту стандартизации предприятие (организация)-разработчик направляет ему проект стандарта на отзыв, а по решению Госстандарта России (Госстроя России) и на согласование.

Примечание - Согласование проекта стандарта в ТК (ПК) осуществляется в соответствии с 3.4.4.

Принятие и государственная регистрация стандарта

3.5.1 Госстандарт России (Госстрой России) рассматривает проект стандарта, принимает его и вводит в действие Постановлением Госстандарта России (Госстроя России).

Перед принятием стандарта Госстандарт России (Госстрой России) проводит его проверку на соответствие законодательству Российской Федерации, требованиям государственных стандартов, метрологическим правилам и нормам, применяемой терминологии, правилам построения, изложения и оформления стандартов.

При принятии стандарта устанавливают дату его введения в действие с учетом мероприятий, необходимых для внедрения стандарта. Срок действия стандарта, как правило, не устанавливают.

3.5.2 Государственную регистрацию стандарта осуществляет Госстандарт России в установленном им порядке.

Издание стандарта

3.6.1 Госстандарт России публикует информацию о принятых стандартах в ежемесячном информационном указателе «Государственные стандарты Российской Федерации».

Госстандарт России и Госстрой России издают и распространяют стандарты в установленном ими порядке.

Вопрос № 36

«Какие документы относятся к нормативным?»

 

37 вопрос: Полным факторным экспериментом (ПФЭ) называется эксперимент, реализующий все возможные неповторяющиеся комбинации уровней п независимых управляемых факторов, каждый из которых варьируют на двух уровнях [4]. Число этих комбинаций N = 2 ⁿ определяет тип ПФЭ. Для упрощения дальнейшее изложение построим на примере планирования типа N = 2³, т.е. на примере объекта с тремя (n = 3) независимыми управляемыми факторами x ₁, х ₂, х ₃. При планировании эксперимента проводят преобразование размерных управляемых независимых факторов х_i в безразмерные (нормированные)

. (4)

Это дает возможность легко построить ортогональную матрицу планирования (МП) и значительно облегчает дальнейшие расчеты, так как в этом случае верхние и нижние уровни варьирования z_{i в} и z_{i н} в относительных единицах равны соответственно +1 и –1 независимо от физической природы факторов, значений основных уровней x_{i в} и x_{i н} и интервалов варьирования факторов D х_i.

Например, пусть некоторый входной фактор (допустим, температура) имеет номинальное значение , интервал варьирования . Тогда верхнему уровню варьирования будет соответствовать, согласно формуле (4), нормированное значение , а нижнему уровню – нормированное значение .

Если для трехфакторной задачи теоретическое уравнение регрессии относительно нормированных факторов имеет вид

, (5)

(т.е. степенями факторов выше первой можно пренебречь), то ПФЭ дает возможность найти раздельные (не смешанные друг с другом) оценки коэффициентов b _i. Так как изменение выходной величины у носит случайный характер, то имеется возможность определить лишь выборочные коэффициенты регрессии b_i, b_il для оценивания теоретических коэффициентов b _i, b _il. Процесс нахождения модели (идентификации) методом ПФЭ состоит из: 1) планирования эксперимента; 2) проведения эксперимента на объекте исследования; 3) проверки воспроизводимости (однородности выборочных дисперсий эксперимента; 4) получения математической модели объекта с проверкой статистической значимости оценок выборочных коэффициентов регрессии; 5) проверки адекватности математического описания.

Планирование эксперимента. Матрицу планирования ПФЭ для рассматриваемого примера (n = 3) можно представить в виде табл. 1.

 

Таблица 1

 

g	z 0	z 1	z 2	z 3	z 1 z 2	z 1 z 3	z 2 z 3	z 1 z 2 z 3
	+1 +1 +1 +1 +1 +1 +1 +1	–1 +1 –1 +1 –1 +1 –1 +1	–1 –1 +1 +1 –1 –1 +1 +1	–1 –1 –1 –1 +1 +1 +1 +1	+1 –1 –1 +1 +1 –1 –1 +1	+1 –1 +1 –1 –1 +1 –1 +1	+1 +1 –1 –1 –1 –1 +1 +1	–1 +1 +1 –1 +1 –1 –1 +1

 

Ее составляют по следующим правилам.

1 Каждая g -я строка матрицы содержит набор координат z_ig точки, в которой проводится g -й опыт (i = 1, 2,..., п; g = 1, 2,..., N).

2Вводят фиктивную переменную z ₀= +1 для определения свободного члена 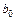уравнения регрессии.

3 Поскольку переменные z_i принимают лишь значения +1 и –1, все взаимодействия z_iz_l (i, l = 1, 2, 3; i ¹ l) могут принимать только такие же значения.

4 В первой строке (g = 1) все управляемые факторы выбирают на нижнем уровне, т.е. z_i = –1. Последующие g -e варианты варьирования при составлении МП выбирают так: при построчном переборе всех вариантов частота смены знака факторов для каждого последующего фактора z_{i +1} вдвое меньше, чем для предыдущего z_i (см. табл. 1), т.е. знаки первого столбца чередуются через один, второго – через два, третьего – через четыре.

Три столбца управляемых факторов образуют собственно план эксперимента (обведено жирной чертой в табл. 1), а остальные столбцы МП получаются перемножением соответствующих значений управляемых факторов и необходимы для расчета оценок соответствующих коэффициентов при взаимодействиях.

Аналогично могут быть получены планы для сколь угодно большого числа п независимых управляемых факторов.

Проведение эксперимента на объекте исследования. Так как изменение отклика y носит случайный характер, то в каждой точке приходится проводить т параллельных опытов и результаты наблюдений y_{g 1}, y_{g 2},..., y_gm усреднять:

. (6)

Пусть в рассматриваемом случае число параллельных опытов в каждой строке МП m = 3. Перед реализацией плана на объекте необходимо рандомизировать (расположить в случайном порядке) варианты варьирования факторов, т.е. с помощью таблицы равномерно распределенных случайных чисел или компьютерной программы для проведения процесса рандомизации определить последовательность реализации вариантов варьирования плана в N ´ m опытах.

Далее проводят эксперимент, и результаты наблюдений эксперимента соответственно вариантам варьирования плана записывают в столбцы табл. 2, а в столбце записывают осредненные значения.

Получение математической модели объекта. При ПФЭ получаются независимые оценки b ₀, b_i, b_il соответствующих коэффициентов модели b₀, b _i, b _il, т.е. b ₀ ® b₀, b_i ® b _i, b_il ® b _il. Эти оценки легко найти по формулам

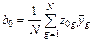, , , (12)

, . (13)

Для нашего примера, используя данные табл. 1 и 2, получим:

;

;

; ;

;

; ; .

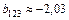38 вопрос: Дробным факторным экспериментом (ДФЭ) называется эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента. ДФЭ позволяет получить, например, линейное приближение искомой функциональной зависимости в некоторой небольшой окрестности точки базового режима при минимуме опытов.

Планирование эксперимента. Для решения трехфакторной (п = 3) задачи регрессии в линейном приближении можно ограничиться четырьмя вариантами варьирования, если в планировании ПФЭ типа N = 2² произведение z ₁ z ₂ приравнять третьему независимому фактору z ₃. Такое планирование, представленное матрицей (табл. 5), позволяет найти свободный член b ₀ и три оценки коэффициентов регрессии при линейных членах b ₁, b ₂, b ₃ (из четырех опытов нельзя получить более четырех оценок коэффициентов регрессии).

 

Таблица 5

 

g	z 0	z 1	z 2	z 3	z 1 z 2	z 1 z 3	z 2 z 3	z 1 z 2 z 3
	+1 +1 +1 +1	–1 +1 –1 +1	–1 –1 +1 +1	+1 –1 –1 +1	+1 –1 –1 +1	–1 –1 +1 +1	–1 +1 –1 +1	+1 +1 +1 +1

 

Применение ДФЭ всегда связано со смешиванием, т.е. с совместным оцениванием нескольких теоретических коэффициентов математической модели. В рассматриваемом случае, если коэффициенты регрессии b _il при парных произведениях отличны от нуля, каждый из найденных коэффициентов b_i служит оценкой двух теоретических коэффициентов регрессии:

b ₀ ® b₀ + b₁₂₃; b ₁ ® b₁ + b₂₃; b ₂ ® b₂ + b₁₃; b ₃ ® b₃ + b₁₂.

Это означает, что, найдя по результатам эксперимента оценку, например, 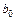, мы реально получим "сумму" двух коэффициентов и .

Действительно, указанные теоретические коэффициенты в таком планировании не могут быть оценены раздельно, поскольку столбцы МП для линейных членов и парных произведений совпадают (полностью коррелированны). Рассмотренный план ДФЭ представляет половину плана ПФЭ типа 2³ и называется полурепликой от ПФЭ типа 2³ или планированием типа N = 2^3-1(см. табл. 5).

Для правильного планирования ДФЭ необходимо использовать все полученные ранее сведения теоретического и интуитивного характера об объекте и выделить те факторы и произведения факторов, влияние которых на отклик существенно. При этом смешивание нужно производить так, чтобы линейные коэффициенты b₀, b₁,..., b _n были смешаны с коэффициентами при взаимодействиях самого высокого порядка (так как обычно они в модели отсутствуют) или при тех взаимодействиях, о которых априори известно, что они не оказывают влияния на отклик. Следовательно, недопустимо произвольное разбиение плана ПФЭ типа 2³ на две части для выделения полуреплики типа 2^3-1.

При большом числе п факторов для получения линейного приближения можно построить дробные реплики высокой степени дробности. Так, при п = 7 можно составить дробную реплику на основе ПФЭ типа 2³, приравняв четыре из семи факторов к взаимодействиям трех других факторов: парным и тройному. Будем обозначать тип дробной реплики записью 2 ^{n – p} , если р факторов приравнены к произведениям остальных n – р факторов.

План ДФЭ можно построить, приравнивая факторы различным взаимодействиям (парным, тройным и т.д.). Разумеется, при этом меняется система совместных оценок теоретических коэффициентов. Для получения системы совместных оценок и анализа разрешающей способности дробных реплик удобно пользоваться понятиями генерирующего и определяющего соотношений.

Генерирующее соотношение служит для построения дробной реплики. Так, в рассмотренном планировании мы задавали полуреплику плана ПФЭ типа 2³ с помощью генерирующего соотношения z ₃ = z ₁ z ₂.

Определяющим соотношением называется соотношение, задающее элементы первого столбца матрицы планирования для фиктивной переменной (все они всегда равны +1). Выражение определяющего соотношения в рассматриваемом случае получается умножением левой и правой частей приведенного генерирующего соотношения на z ₃ (элемент, стоящий в левой части), т.е. 1 = z ₁ z ₂ z ₃, так как всегда .

Знание определяющего соотношения позволяет найти всю систему совместных оценок без изучения матрицы планирования ДФЭ. Соотношения, задающие эти оценки, можно найти, последовательно перемножив независимые факторы на определяющее соотношение:

z ₀ = z ₁ z ₂ z ₃; z ₁ = z ₂ z ₃; z ₂ = z ₁ z ₃; z ₃ = z ₁ z ₂.

Отсюда легко находятся смешиваемые теоретические коэффициенты регрессии и их оценки:

b ₀ ® b₀ + b₁₂₃; b ₁ ® b₁ + b₂₃; b ₂ ® b₂ + b₁₃; b ₃ ® b₃ + b₁₂.

Если априори можно принять, что коэффициенты при всех парных и тройном взаимодействии равны нулю, то реализация этой полуреплики позволит получить раздельные оценки для всех четырех линейных коэффициентов регрессии. Разрешающая способность полуреплик определяется их генерирующими соотношениями. Разрешающая способность тем выше, чем более высок порядок взаимодействий, с коэффициентами которых смешаны линейные коэффициенты. Она увеличивается для главных полуреплик с ростом числа независимых факторов.

Например, требуется построить полуреплику ПФЭ для исследования объекта с четырьмя независимыми факторами z ₁, z ₂, z ₃ и z ₄. Для этого можно использовать генерирующее соотношение . Умножив обе его части на , получим определяющее соотношение . Далее, умножая выбранное определяющее соотношение на одиночные факторы , определим для них систему совместных оценок:

; ; ; ; .

Таким образом, оценка коэффициента будет смешана с оценкой (одинаковые строки в МП), – с и т.д. Если требуется получить систему совместных оценок для парных взаимодействий, то необходимо аналогично умножить обе части определяющего соотношения последовательно на каждое парное взаимодействие . Например, для получим , а, следовательно, оценка коэффициента будет смешана с оценкой .

 

39 вопрос: Контрольный листок (таблица проверок) позволяет ответить на вопрос: «Как часто случается определенное событие?» С него начинается превращение мнений и предположений в факты. Построение контрольного листка включает в себя следующие шаги, предусматривающие необходимость:

1) установить как можно точнее, какое событие будет наблюдаться. Каждый должен следить за одной и той же вещью;

2) договориться о периоде, в течение которого будут собираться данные. Он может колебаться от часов до недель;

3) построить форму, которая будет ясной и легкой для заполнения. В форме должны быть четко обозначены графы и колонки, должно быть достаточно места для внесения данных;

4) собирать данные постоянно и честно, ничего не искажая. Еще раз убедитесь, что назначенное вами время достаточно для выполнения задачи по сбору данных.

Собранные данные должны быть однородными. Если это не так, то необходимо в начале сгруппировать данные, а затем рассматривать их по отдельности.

Гистограмма применяется, когда требуется исследовать и представить распределение данных о числе единиц в каждой категории с помощью столбикового графика.

Как мы уже видели на диаграмме Парето, очень полезно представить в форме столбикового графика частоту, с которой появляется определенное событие (так называемое частотное распределение). Однако диаграмма Парето имеет дело только с характеристиками продукции или услуги: типами дефектов, проблемами, угрозой безопасности и т. п.

Гистограмма, напротив, имеет дело с измеряемыми данными (температура, толщина) и их распределением. Распределение может быть критическим, т.е. иметь максимум. Многие повторяющиеся событиядают результаты, которые изменяются во времени.

Гистограмма обнаруживает количество вариаций, которые имеет процесс. Типичная гистограмма может выглядеть так, как показано ниже на рисунке.

Количество классов (столбиков на графике) определяется тем, как много взято образцов или сделано наблюдений.

Некоторые процессы по своей природе искажены, несимметричны, поэтому не следует ожидать, что каждое распределение будет иметь форму колоколообразной кривой.

Не доверяйте точности данных, если классы внезапно остановились на какой-то точке, например границе спецификации, хотя перед этим и число не уменьшалось.

Если у кривой имеется два пика, это означает, что данные собраны из двух или более различных источников, т. е. смен, машин и т. п.

Диаграмма Парето применяется, когда требуется представить относительную важность всех проблем или условий с целью выбора отправной точки для решения проблем, проследить за результатом или определить основную причину проблемы.

Диаграмма Парето — это особая форма вертикального столбикового графика, которая помогает определить, какие имеются проблемы, и выбрать порядок их решения. Построение диаграммы Парето, основанное или на контрольных листках, или на других формах сбора данных, помогает привлечь внимание и усилия к действительно важным проблемам. Можно достичь большего, занимаясь самым высоким столбиком, не уделяя внимание меньшим столбикам

Порядок построения диаграммы Парето.

1. Выберите проблемы, которые необходимо сравнить, и расположите их в порядке важности (путем мозговой атаки, используя существующие данные — отчеты).

2. Определите критерий для сравнения единиц измерения (натуральные характеристики, стоимостные).

3. Наметьте период времени для изучения.

4. Сгруппируйте данные по категориям, сравните критерии каждой группы.

5. Перечислите категории слева направо на горизонтальной оси в порядке уменьшения значения критерия. В последний столбик включите категории, имеющие наименьшее значение.

 

40 вопрос: Контроль по количественному признаку. Среднее значение и размах

 

Одним из способов достижения удовлетворительного качества и

поддержания его на этом уровне является применение контрольных карт.

Наибольшее распространение получили контрольные карты среднего

значения [pic] и контрольные карты размаха R, которые используются

совместно или раздельно.

Приведем пример. В сосудах 1,2,3,… находятся деревянные палочки, на

которых нанесены числа –10,-9,…,-2,-1,0,1,2,…,9,10. Палочки имитируют

изделия, а нанесенные на них числа означают отклонения контролируемого

размера от номинального в сотых долях процента. В каждом сосуде находится N

палочек, которые можно рассматривать как изделия, изготовленные за заданный

интервал времени, называемый периодом отбора выборок или проб. Значения N

предполагается большим, так что на нескольких палочках может быть нанесено

одно и тоже число, некоторые палочки могут быть единственными носителями

определенных чисел, более того, возможно, что в каком-нибудь сосуде не

окажется вообще палочки с определенным числом. После тщательного

перемешивания палочек в сосудах извлекается из каждого сосуда выборка

объемом n палочек, например n=5. При этом тщательное перемешивание

обеспечивает случайность выбора палочек. Записав числа, нанесенные на

оказавшихся в очередных выборках палочках, подсчитывают их средние

арифметические значения и наносят как ординату точки с абсциссой,

соответствующей номеру сосуда. Если точка окажется внутри начерченных на

контрольной карте границ, то имитируемый описанной моделью процесс

считается налаженным, в противном случае – требующим корректировки.

Статистикой принято называть функцию случайных величин, полученных из

одной совокупности, которая используется для оценки определенного параметра

этой совокупности.

Пусть взято двадцать пять выборок, состоящих из пяти образцов каждая.

Среднее арифметическое значение и размах определяются для каждой выборки

отдельно. Они наносятся на контрольные карты средних арифметических

значений и размахов.

 

2 Контрольные карты. Контроль по альтернативному признаку

Эти карты используются при контроле по альтернативному признаку. Это

значит, что после проверки изделие считается либо годным, либо дефектным и

решение о качестве контролируемой совокупности принимают в зависимости от

числа обнаруженных в выборке или пробе дефектных изделий или от числа

дефектов, приходящихся на определенное число изделий (единиц продукции).

Дефект – это каждое отдельное несоответствие продукции установленным

требованиям.

Брак – это продукция, передача которой потребителю не допускается из-

за наличия дефектов.

Наиболее распространенными для метода учета дефектов являются контроль

качества доли дефектных единиц продукции, называемые р-картами и количества

дефектов на единицу продукции, называемые с-картами.

Понятие доли дефектных единиц продукции употребляется в том случае,

когда имеется в виду доля дефектных единиц продукции в совокупности

дефектных и годных единиц.

Тогда р определяется следующим образом: р (доля дефектных единиц

продукции) равно общему количеству обнаруженных дефектных изделий,

деленному на общее количество проверенных изделий.

[pic]

Понятие количества дефектов на единицу продукции используется тогда,

когда изделие не считается ни браком, ни годным, а определяется только

количеством дефектов в изделии.

Таким образом, с (количество дефектов на единицу продукции) равно

общему количеству обнаруженных дефектов, деленному на общее количество

проверенных изделий.

[pic]

Характеристики р и с являются статистическими оценками совокупности р’

и с’.

 

41 вопрос: Потребитель, как правило, не имеет возможности контролировать качество

продукции в процессе ее изготовления. Тем не менее, он должен быть уверен,

что получаемая им от изготовителя продукция соответствует установленным

требованиям, и, если это не подтвердится, он вправе потребовать от

изготовителя замены брака или устранения дефектов.

Основным методом контроля поступающих потребителю сырья, материалов и

готовых изделий является статистический приемочный контроль качества

продукции.

Статистический приемочный контроль качества продукции – выборочный

контроль качества продукции, основанный на применении методов

математической статистики для проверки качества продукции установленным

требованиям.

Если при этом объем выборки становится равным объему всей

контролируемой совокупности, то такой контроль называют сплошным. Сплошной

контроль возможен только в тех случаях, когда в процессе контроля качество

продукции не ухудшается, в противном случае выборочный контроль, т.е.

контроль определенной небольшой части совокупности продукции, становится

вынужденным.

Сплошной контроль проводится, если к тому нет особых препятствий, в

случая возможности наличия критического дефекта, т.е. дефекта, наличие

которого полностью исключает использование продукции по назначению.

Можно проверить все изделия также и при следующих условиях:

. партия изделий или материала невелика;

. качество входного материала плохое или о нем ничего не известно.

Можно ограничиться проверкой части материала или изделий, если:

. дефект не вызовет серьезной неисправности оборудования и не создает

угрозу жизни;

. изделия используются группами;

. бракованные изделия можно обнаружить на более поздней стадии сборки.

 

 

42 вопрос: Дерево - инструмент познания (краткая историческая справка)

Обычно иерархические структуры типа дерево (д.) применяются для анализа возможности решения некоторой сложной проблемы. В квалиметрии регламентирован комплекс правил (их около 30), следование которым позволяет различным разработчикам, применительно к одному и тому же конкретному объекту получать одно и то же д., (что является необходимым условием достоверности получаемых с помощью этого д. результатов). Основные из этих правил кратко излагаются ниже.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: