 |
Равномерное вращение сосуда с жидкостью
|
|
|
|
Сила давления жидкости на плоскую стенку
Используем основное уравнение гидростатики (2.1) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.8).
 |
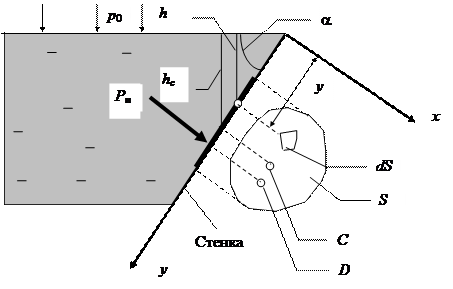Рис. 2.8
Вычислим полную силу P давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
Ось 0 x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 0 y – перпендикулярно этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:
,
где p 0 – давление на свободной поверхности; h – глубина расположения площадки dS.
Для определения полной силы P выполним интегрирование по всей площади S:
,
где y – координата центра площадки dS.
Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси Ox и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.
.
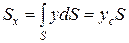Следовательно,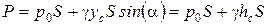 
, где h c – глубина погружения центра тяжести площади S. В результате имеем:
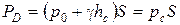, (2.6)
т. е. полнаясила давления жидкости на плоскую стенку равна произведению гидростатического давления (определяемого давлением на свободной поверхности жидкости и глубиной погружения центра тяжести площади S) в центре тяжести площади этой стенки на ее площадь.
Найдем положение точки приложения силы избыточного давления.
Так как внешнее давление p 0 передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S: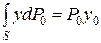 
; 
; 
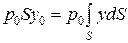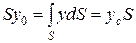, т.е. 
.
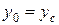Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, согласно которому момент равнодействующей силы давления относительно оси 0 x равен сумме моментов составляющих сил:
|
|
|
; 
; 
,
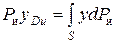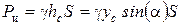где yDи – координата точки приложения силы P и.
Выразим yDи:
,
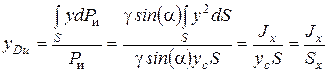где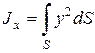 
– момент инерции площади S относительно оси 0 x.
Учитывая, что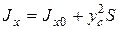 
(Jx0 – момент инерции площади S относительно оси, проходящей через центр тяжести площади S и параллельной 0 x), получим
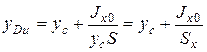. (2.7)
Таким образом, точка приложения силы P и расположена ниже центра тяжести площади стенки на расстояние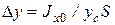 
.
Определим центр давления yD от действия сил давления на свободной поверхности и избыточного давления. Запишем уравнение моментов относительно верхней точки пластины и определим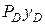 
как результирующий момент от действия моментов перечисленных выше сил давления.
 |
; 
.
.
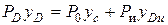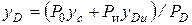Рис. 2.9
В частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится из геометрических соображений. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.10), центр тяжести которого отстоит от основания на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на том же расстоянии от основания: 
, 
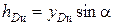. Если стенка вертикальная, то .
Рис. 2.10
| В машиностроении часто приходится сталкиваться с действием силы давления на плоские стенки, например на стенки поршней или цилиндров гидравлических машин. Обычно p 0 при этом бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки. Найдем статические моменты, моменты инерции и положения центров тяжести для прямоугольной и треугольной пластин. |
Закон Архимеда
Пусть в жидкость погружен параллелепипед объемом W (рис. 2.13).
|
|
|
 |
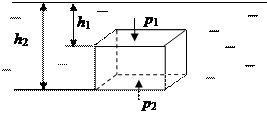Рис. 2.13
На него действуют следующие силы: сверху сила давления от столба жидкости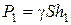 
, снизу – 
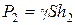, где S – площади нижней и верхней граней параллелепипеда; равнодействующая сил давлений, действующих на боковые грани, равна нулю, так как они равны и противоположно направлены. Спроектируем силы на вертикальную ось, вес тела учитывать не будем. Отметим, что согласно закону Паскаля давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково, поэтому давление на внешней поверхности действует по всем граням одинаково и во взаимно противоположных направлениях, поэтому результирующая сила равна нулю.
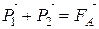, откуда
; 
.
Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.
В случае тела произвольной формы, погруженного в жидкость, закон Архимеда выводится, привлекая дополнительные рассуждения.
Равномерное вращение сосуда с жидкостью
Вращение сосуда с жидкостью вокруг вертикальной оси
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.15).
 |
Рис. 2.15
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и 
. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Учитывая, что сила 
нормальна к свободной поверхности, получим 
, отсюда 
или после интегрирования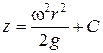 
.
В точке пересечения свободной поверхности с осью вращения C = h и r =0, поэтому окончательно будем иметь
|
|
|
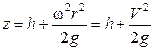, (2.10)
где 
.
Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):
.
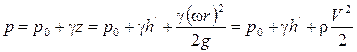Вращение сосуда с жидкостью вокруг горизонтальной оси
При таком вращении угловая скорость w столь велика, что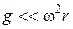 
(действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давления и центробежная сила.
 |
Рис. 2.16
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp (разложили p в ряд Тейлора, но так как в данном случае p зависит только от r, то dr / dr сократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса
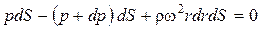или 
.
После интегрирования получим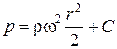 
. Постоянную C найдем из условия, что при r = r 0 p = p 0, следовательно, 
.
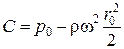Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
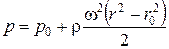. (2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
,
а затем следует выполнить интегрирование в требуемых пределах:
.
Если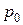 
равно внешнему давлению, то 
.
При большой скорости вращения жидкости получается значительная суммарная сила давления F б на боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
|
|
|
Приведем выражение для определения силы F б без вывода:
, где 
– длина цилиндра.
|
|
|
