 |
Турбулентное течение в каналах постоянного сечения
|
|
|
|
Структура при турбулентном движении жидкости иная, чем при ламинарном (рис. 4.8). Если рассматривать поперечное сечение потока в трубе, то у стенки трубы мы имеем пограничный слой, а за пограничным слоем – турбулентное ядро течения. Пограничный слой состоит из ламинарного подслоя 
, в котором течение жидкости происходит в ламинарном режиме, и переходного 
, в котором происходит переход из ламинарного режима течения в турбулентный. Пограничный слой имеет толщину от 0,1 мм до нескольких миллиметров. При увеличении скорости потока толщина ламинарного подслоя уменьшается, так как оказывается, что число Рейнольдса для ламинарного подслоя есть величина постоянная – 
.
На распределение скоростей по живому сечению при турбулентном режиме течения влияет шероховатость стенок, ограждающих поток. Шероховатость является одной из причин появления вихрей у стенок и дополнительных гидравлических сопротивлений, а, следовательно, и потерь энергии при движении потока. Для оценки выступов шероховатости в гидравлике введено понятие абсолютной шероховатости (
). Абсолютная шероховатость характеризуется высотой среднего выступа шероховатой поверхности . При этом важен не абсолютный размер бугорков, а отношение 
(
) – относительная шероховатость (
– относительная гладкость). Одна и та же абсолютная шероховатость может совершенно не оказывать влияние на сопротивление трубы большого диаметра, но способна существенно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейший случай, – когда бугорки одинакового размера и формы (равномерно-зернистая шероховатость).
Если ламинарный подслой покрывает выступы шероховатости, то труба считается гидравлически гладкой, а если нет,– гидравлически шероховатой. Ввиду того, что геометрические характеристики абсолютной шероховатости не могут в достаточной степени определять сопротивление трубы, введено понятие о гидравлически эквивалентной равномерно-зернистой шероховатости Δэ, которая создает такое же сопротивление, как реальная шероховатость.
|
|
|
При турбулентном движении скорости (мгновенные) отдельных частиц жидкости (макрообъемов) в отдельных точках пространства все время меняются по величине и направлению, т.е. происходит пульсация скоростей. Однако мгновенные скорости в данной точке пространства колеблются около осредненной скорости. Аналогично происходит и пульсация давления по величине.
Установившимся движением при турбулентном течении называют такое движение, при котором в любой точке пространства, занятого жидкостью, осредненная скорость и гидродинамическое давление не меняются с течением времени.
 |
|
рис. 4.8
В турбулентном потоке, кроме продольного поступательного движения частиц жидкости, существует еще и поперечное, которое приводит к перемешиванию макрообъемов жидкости, в результате чего появляются дополнительные потери энергии и возникают дополнительные касательные напряжения.
Для ламинарного режима касательные напряжения равны
.
При турбулентном движении:
,
где l – путь смещения, он определяется экспериментально для различных параметров течения, зон и геометрии каналов (вблизи стенок труб 
, K =0,435, x – расстояние от сечения зарождения турбулентного течения до рассматриваемого сечения).
Первый член в последнем выражении характеризует вязкое трение при ламинарном движении, второй – выражает дополнительное касательное напряжение от пульсаций, возникающих при поперечном движении макрообъемов жидкости. С увеличением скорости течения (Re) главное влияние на величину касательных напряжений оказывает второй член и при больших Re касательные напряжения (а, значит, и потери полного напора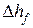 
) оказываются пропорциональны квадрату градиента скорости.
|
|
|
Обычно под термином вязкие напряжения подразумевают касательные напряжения при ламинарном режиме течения (вязкое трение), а под термином касательные напряжения – напряжения при турбулентном течении (вязкие и дополнительные касательные напряжения).
рис. 4.9 Рис. 4.10
1. При ламинарном режиме 
, 
.
2. При турбулентном режиме 
, 
– для гидравлически гладких труб; 
– для гидравлически шероховатых.
Для развитого турбулентного режима 
, т.е. пренебрегаем трением при ламинарном движении.
Характерная зависимость потерь полного напора для различных режимов течения приводятся на рис. 4.10.
При турбулентном режиме течения потери в круглых трубах определяются по формуле Дарси в виде:
,
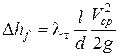где λт – определяется по зависимостям для турбулентного течения (см. ниже).
В трубах с некруглым сечением в первом приближении – с использованием гидравлического диаметра в виде:
.
Для более точного определения потерь – с использованием гидравлического диаметра и поправочного коэффициента 
, учитывающего форму сечения:
,
где 
(например, для труб квадратного сечения при Re > 2300 – 
и 
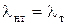); при этом 
.
4.8. О коэффициенте гидравлических сопротивлений трения 
Как показали эксперименты 
. Но эта зависимость при разных условиях движения потока жидкости меняет свою закономерность.
При малых значениях Re, 
, при больших значениях Re, 
, при промежуточных значениях 
. На рис. 4.11 представлены результаты экспериментальных исследований коэффициента сопротивления (И.И. Никуразде) для труб с искусственной равномерно-зернистой шероховатостью. Результаты исследований для труб с неравномерной шероховатостью приводить не будем. Их отличия от результатов для труб с искусственной шероховатостью заключаются в некотором изменении значений граничных чисел Re для различных режимов течения и другими формулами для определения коэффициента сопротивления (это будет указано в тексте).
|
= 
~ 
|
|
|
|
= f (Re)
|
|
|
|
рис. 4.11
Первая область соответствует прямой I-I и относится к ламинарному движению жидкости при Re<2300. Здесь 
.
Вторая область соответствует прямой II-II и относится к турбулентному движению жидкости. Это область гидравлически гладких труб ( < 
л), она имеет место при 
для неравномерной шероховатости реальных труб и 
для равномерной шероховатости (по данным И.Е. Идельчика). При этом для стенок с неравномерной шероховатостью необходимо, чтобы 
, 
, в противном случае имеет место первая переходная зона (см. ниже).
Формула Блазиуса: 
при Re = 2300…105 (равномерно-зернистая шероховатость).
Как видно из формулы Блазиуса, при турбулентном движении на потери в основном влияют процессы, связанные с перемешиванием потока и рассеиванием кинетической энергии вследствие вихреобразования. Вязкость жидкости играет менее существенную роль, так как она в степени 1/4. Также из этой формулы видно, что, так как число Re в степени -1/4, то и скорость в λт тоже в степени ‑1/4, поэтому при подстановке λт в формулу для потерь (Дарси) скорость будет в степени 2-1/4=1,75.
Формула Конакова: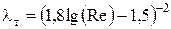 
при Re < 107 (равномерная и неравномерная шероховатость).
 |
рис. 4.12
Третья область располагается правее кривой III-III, она имеет место при 
для неравномерной шероховатости и 
для равномерной шероховатости. Это область квадратичных сопротивлений (автомодельная область). Кривая λт параллельна оси абсцисс (Re).
В этой области вследствие больших скоростей, а, значит, и чисел Рейнольдса толщина ламинарного подслоя уменьшается настолько, что бугорки шероховатости выступают за его толщину и обтекаются турбулентным потоком с вихреобразованием за каждым бугорком. Этим и объясняется квадратичный закон сопротивления, характерный для этой области.
Формула Никуразде: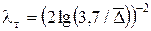 
(равномерная и неравномерная шероховатость).
Формула Б.Л. Шифринсона: 
(равномерная шероховатость),
|
|
|
где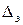 
– эквивалентная абсолютная шероховатость (приводится в таблицах).
Первая переходная зона располагается между прямыми I-I и II-II и соответствует переходу от ламинарного к турбулентному режиму течения (Re=2300-4000 для равномерно-зернистой шероховатости). Для неравномерной шероховатости Reкр<Re<Re2. В этой области λт возрастает с увеличением Re.
Вторая переходная зона располагается между прямыми II-II и III-III (область гидравлически шероховатых труб), она имеет место для неравномерной шероховатости при 
и для равномерно-зернистой шероховатости при 
.
Формула Френкеля: 
.
Формула А.Д. Альтшуля (равномерная и неравномерная шероховатость):
или 
.
|
|
|
