 |
Минимизация логических функций
|
|
|
|
Студент должен:
Знать:
· Методы минимизации логических функций.
Уметь:
· Выполнять минимизацию функций методом непосредственных преобразований; Выполнять минимизацию функций методом непосредственных преобразований;
· Выполнять минимизацию функций с помощью карт Карно.
Метод непосредственных преобразований
Логическая функция, задающая принцип построения схемы цифрового устройства, может быть, как было показано выше, представлена в виде таблицы истинности или в виде СДНФ или СКНФ и может быть использована для получения логической схемы устройства. Однако полученная логическая схема, как правило, не будет оптимальна. Поэтому важным этапом синтеза логических схем является минимизация логических функций.
Минимизация (упрощение формы записи) функции является важной операцией при синтезе логической схемы, так как благодаря предварительно проведенной минимизацией схема реализуется с наименьшим числом элементов.
Для минимизации разработан ряд методов. Одним из простых методов минимизации является метод непосредственных преобразований, который осуществляется с использованием основных теорем алгебры логики.
Например, логическую функцию

в виде СДНФ, можно минимизировать следующим образом:
1. Добавим к данной функции слагаемое  , которое уже есть в данной функции, используя правило х+х=х
, которое уже есть в данной функции, используя правило х+х=х

2. Применим метод склеивания одинаково подчеркнутых элементарных конъюнкций

3. Применим метод склеивания для двух последних элементарных конъюнкций
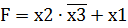
Полученная в результате минимизации логическая функция называется тупиковой. Логическая функция может иметь несколько тупиковых форм.
Выявление и устранить избыточности в записи функции путем её преобразований с использованием аксиом, законов, тождеств и теорем алгебры логики требуют громоздких выкладок и связаны с большой затратой времени.
|
|
|
Карты Карно
Метод непосредственных преобразований наиболее пригоден для простых формул, когда последовательность преобразований очевидна для исполнителя. Наиболее часто этот метод применяется для окончательной минимизации выражений, полученных после минимизации их другими методами.
Стремление к алгоритмизации поиска соседних элементарных произведений привело к разработке табличных методов минимизации логических функций. Одним из них является метод, основанный на использовании карт Карно.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
Карта Карно — это графическое представление таблицы истинности логических функций. Она представляет собой таблицу, содержащую по 2n прямоугольных ячеек, где n — число логических переменных.
Например, карта Карно для функции четырех переменных имеет 24 = 16 ячеек.

Структура карты Карно для функций двух переменных показана на рисунке 2.2. 2
а) б)
а) таблица истинности; б) структура карты Карно
Рисунок 2.2

На рисунке 2.3 представлена структура карты Карно для функции трёх переменных.
а) таблица истинности; б) структура карты Карно
Рисунок 2.3
Карта размечается системой координат, соответствующих значениям входных переменных. Например, верхняя строка карты для функции трех переменных (рисунок 2.3) соответствует нулевому значению переменной x1, а нижняя — ее единичному значению.
Каждый столбец этой карты характеризуется значениями двух переменных: х2 и х3. Комбинация цифр, которыми отмечается каждый столбец, показывает, для каких значений переменных х2 и х3 вычисляется функция, размещаемая в клетках этого столбца.
|
|
|
Если на указанном наборе переменных функция равна единице, то ее СДНФ обязательно содержит элементарное произведение, принимающее на этом наборе единичное значение. Таким образом, ячейки карты Карно, представляющие функцию, содержат столько единиц, сколько элементарных произведений содержится в ее СДНФ, причем каждой единице соответствует одно из элементарных произведений.
Обратим внимание на то, что координаты строк и столбцов в карте Карно следуют не в естественном порядке возрастания двоичных кодов, а в порядке 00, 01, 11, 10. Изменение порядка следования наборов сделано для того, чтобы соседние наборы были соседними, т.е. отличались значением только одной переменной.
Ячейки, в которых функция принимает значения, равные единице, заполняются единицами. В остальные ячейки записываются нули.
Процесс минимизации рассмотрим на примере, представленном на рисунке 2.4.

а) таблица истинности; б) карта Карно
Рисунок 2.4
Сначала формируем прямоугольники, содержащие по 2k ячеек, где k — целое число.
В прямоугольники объединяются соседние ячейки, которые соответствуют соседним элементарным произведениям.
Например, на рисунке 2.4,б объединены ячейки с координатами 001 и 101. При объединении этих ячеек образовался прямоугольник, в котором переменная x1 изменяет свое значение. Следовательно, она исчезнет при склеивании соответствующих элементарных произведений и останутся только х2 и х3, причем переменную х2 берем в инверсном виде, т.к. она равна 0.
Ячейки, расположенные в первой строке (рисунок 2.4 б), содержат единицы и являются соседними. Поэтому все они объединяются в прямоугольник, содержащий 22 = 4 ячейки.
Переменные х2 и х3 в пределах прямоугольника меняют свое значение; следовательно, они исчезнут из результирующего элементарного произведения. Переменная х1 остается неизменной и равной нулю. Таким образом, элементарное произведение, полученное в результате объединения ячеек первой строки рисунка 2.4 б, содержит лишь один х1, который берем в инверсном виде, т.к. он равен 0.
Это, в частности, следует из того, что четырем ячейкам первой строки соответствует сумма четырех элементарных произведений:
|
|
|

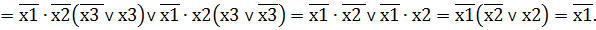
Двум ячейкам сторого столбца соответствует сумма двух произведений

Функция, соответствующая рисунку 2.4 имеет вид:

Совокупность прямоугольников, покрывающих все единицы, называют покрытием. Заметим, что одна и та же ячейка (например, ячейка с координатами 001) может покрываться два или несколько раз.
Итак, можно сделать следующие выводы:
1. Формула, получающаяся в результате минимизации логической функции с помощью карт Карно, содержит сумму стольких элементарных произведений, сколько прямоугольников имеется в покрытии.
2. Чем больше ячеек в прямоугольнике, тем меньше переменных содержится в соответствующем ему элементарном произведении.
Например, для карты Карно, изображенной на рисунке 2.5 а, прямоугольнику, содержащему четыре ячейки, соответствует элементарное произведение  двух переменных, а квадрату, состоящему всего лишь из одной ячейки,— элементарное произведение
двух переменных, а квадрату, состоящему всего лишь из одной ячейки,— элементарное произведение  включающее все четыре переменные.
включающее все четыре переменные.
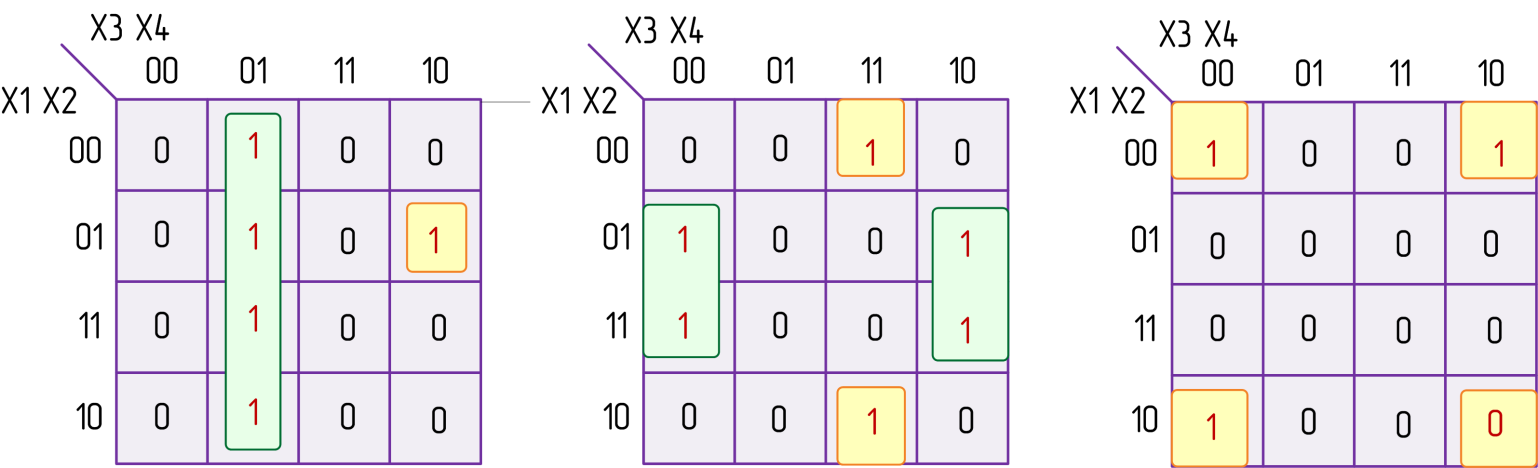
а) б) в)
Рисунок 2.5
Функция, соответствующая покрытию, показанному на рисунке 2.5 а, имеет вид:
 .
.
Несмотря на то, что карты Карно изображаются на плоскости, соседство квадратов устанавливается на поверхности тора. Верхняя и нижняя границы карты Карно как бы «склеиваются», образуя поверхность цилиндра. При склеивании боковых границ получается тороидальная поверхность. Следуя изложенным рассуждениям, устанавливаем, что ячейки с координатами 1011 и 0011, изображенные на рисунке 2.5 б, являются соседними и объединяются в прямоугольник. Действительно, указанным ячейкам соответствует сумма элементарных произведений

Аналогично объединяются и остальные четыре единичные ячейки. В результате их объединения получаем элементарное произведение  .
.
Окончательно функция, соответствующая покрытию, изображенному на рисунке 2.5 б, имеет вид 
Карта Карно, показанная на рисунке 2.5 в, содержит единичные ячейки, расположенные по углам. Все четыре ячейки являются соседними, и после объединения дадут элементарное произведение 
Рассмотренные выше примеры позволяют сформулировать последовательность проведения минимизации логических функций с помощью карт Карно:
|
|
|
1. Изображается таблица для n переменных и производится разметка ее сторон.
2. Ячейки таблицы, соответствующие наборам переменных, обращающих функцию в единицу, заполняются единицами, остальные ячейки — нулями.
3. Выбирается наилучшее покрытие таблицы правильными прямоугольниками, которые обводим контурами. В каждом прямоугольнике должно быть 2n ячеек.
4. Одни и те же ячейки с единицами могут входить в разные контуры.
5. Количество прямоугольников должно быть минимальным, а площадь прямоугольников максимальная.
6. Для каждого прямоугольника записываем произведение только тех переменных, которые не изменяют своего значения. Если эта переменная равна нулю, то ее записывают в инверсном виде.
7. Полученные произведения соединяем знаком логического сложения.
Контрольные вопросы:
1. Что называют минтермами и минтермами?
2.Записать функции, заданные таблицами 2.9 и 2.10 в СДНФ и СКНФ.
Таблица 2.9
| X1 | ||||
| X2 | ||||
| F |
Таблица 2.10
| X1 | ||||
| X2 | ||||
| F |
3. Упростите логические функции, используя аксиомы тождества и законы алгебры логики:
a) 
b) 
c) 
d) 
e) 
f) 
Логические элементы
Студент должен
Знать:
· Таблицы логических состояний для основных функциональных логических схем;
· Основные базисы построения логических схем.
Уметь:
· Определять логические состояния на выходах цифровых схем по известным состояниям на входах;
· Выполнять логическое проектирование в базисах микросхем;
· Выбирать микросхему по справочнику, исходя из заданных параметров и условий использования.
Принцип логического устройства базируется в ИМС на работе биполярных транзисторов в режиме ключа (либо замкнут, либо разомкнут).
| Логические схемы – это функционально законченные устройства, работа которых основана на законах и положениях алгебры логики или Буле или алгебры двоичных чисел основой которых является два числа 0 и 1 независимо от конкретного значения Uпит. |
Логическое действие осуществляется как с одной (одновходовый логический элемент) так и с множеством (многовходовый логический элемент) входных переменных.
При работе логических устройств используются три основных действия согласно алгебры Буля – «И», «ИЛИ», «НЕ».
Логическая функция может быть выражена словесно, в алгебраической форме, таблицей истинности, называемой переключательной таблицей, с помощью временных диаграмм. Рассмотрим все варианты представления логических функций.
|
|
|
|
|
|


