Вычисление последовательностей

Лекция 7

Вычисление последовательностей

Цели:

ü получить представление о типах последовательностей и способах их обработки;

ü освоить методику написания циклических вычислительных алгоритмов для вычисления последовательностей, перевода таких алгоритмов на язык программирования С++ и разработки соответствующего проекта в среде Visual C++ 6. 0.

 

Циклические структуры используются для вычисления элементов рекуррентных последовательностей, обработки массивов, а также решения задач, которые предполагают использование численных методов.

 

4. Примеры вычисления последовательностей

Определение 1. Пусть переменная х принимает последовательно значения х₁, х₂, х₃, …, х_n, …. Такое нумерованное множество чисел называется последовательностью. Закон образования последова-тельности задается формулой n-го члена х_n.

Из данного определения видно, что для задания последовательности нужно знать закон образования n-го члена последовательности, т. е. функцию, которая ставит натуральному числу n в соответствие некоторое значение f(n):  x_n=f(n).

Определение 2. Последовательность  {x_n} называется сходящейся к х*, если при n→ ∞ |x*-x_n|→ 0.

Определение 3. Последовательность {x_n} называется убывающей, если при n→ ∞ |x_n|→ 0.

Определение 4. Последовательность {x_n} называется возрастающей, если при n→ ∞ |x_n|→ ∞.

При вычислении возрастающих последовательностей должно быть задано условие, ограничивающее вычисление элементов такой последовательности.

Определение 5. Пусть дана некоторая последовательность элемент-ов а₁, а₂, а₃, …, а_n, …, причём а_к+1=F(а₁, а₂, … а_n, а_к), а_к+2=F(а₂, а₃,... а_n, а_к, а_к+1). Если функцию F можно определить или она задана, то последовательность а₁, а₂, а₃, …, а_к, а_{к+1, …} называется рекуррентной последовательностью.

Формула n-го члена рекуррентной последовательности (рекуррентная формула) а_n=F(a_n-k, a_n-k+1, а_n-к+2, …, а_n-1), где число k называется глубиной рекурсии и определяет количество предшествующих элементов, необходимых для вычисления а_n. Смысл глубины рекурсии в том, что она показывает, сколько переменных необходимо для вычисления элементов последовательности.

Примеры задач с использованием

рекуррентных последовательностей

 Вычислить заданный n-й элемент последовательности.

Вычислить сумму или произведение n элементов последовательности.

Найти количество элементов на данном отрезке последовательности, удовлетворяющих определенному условию.

Найти номер первого элемента последовательности, удовлетворя-ющего определённому условию.

Пример 1. Вычислить n-й элемент арифметической прогрессии а₁=1, а₂=3, а₃=5 и т. д.

Ход выполнения работы

1. Написание алгоритма решения задачи будет состоять из двух шагов.

Выведем рекуррентную формулу. Так как разность прогрессии равна 2, то рекуррентная формула будет следующей: 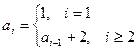. Читается формула так: при i=1 a_i=1; при i≥ 2 a_i=a_i-1+2, т. е. каждый последующий элемент равен сумме предыдущего и 2.

Определим глубину рекурсии. Поскольку каждый следующий элемент вычисляется только через один предыдущий, то глубина рекурсии равна 1. Следовательно, для вычисления элементов последовательности нужны две переменные. Однако в этом случае можно обойтись одной переменной. Для определения значения последующего элемента последовательности будем использовать рекурсивную формулу

 

 

Алгоритм	Программа
объявление цел: а, n, i ввод n //текущий элемент последовательности и //его текущий номер а=1, i=1 //вычисляем элементы последовательности для i=2 до n шаг 1   а=а+2 всё_для i печать а	#include " stdio. h" #include " math. h" int main ( ) { int a, i, n; printf(" n=" ); scanf(" %i", & n); a=1, i=1; for (i=2; i< =n; i++)                a=a+2; printf(" a%i=%i \n", n, a); return 1; }

2.  Написать программу, соответствующую алгоритму:

3.  Создать проект и реализовать данную задачу в среде                Visual C++ 6. 0.

 

Пример 2. Вывести на печать первые n (n≥ 3) чисел Фибоначчи. Распечатать все элементы и подсчитать, сколько среди них четных чисел. Числа Фибоначчи образуются по закону:

а₁=1, а₂=1, …, а_i=a_i-1+a_i-2, ….

Ход выполнения работы

1. Написание алгоритма решения задачи будет состоять из двух шагов.

Рекуррентная формула задается в определении чисел Фибоначчи: .

Глубина рекурсии равна 2, поэтому для вычисления чисел Фибоначчи нужны три переменные.

2. Написать программу, соответствующую алгоритму:

Алгоритм	Программа
объявление цел: i, n, a1, a2, а3, s //ввод количества вычисляемых элементов ввод n //инициализация а1=1, а2=1, s=0 печать а1 печать а2 //цикл для вычисления элементов и суммы для i=3 до n шаг 1 a3= a2+ a1 печать а3 если а2%2=0 //условие четности                       //значения переменной а2    s=s+1 все_если   а1= a2 а2=а3 всё_для i печать s	#include " stdio. h" #include " math. h" int main ( ) { int a1, a2, a3, s, i, n; printf(" n=" ); scanf(" %i", & n); a1=1, a2=1, s=0; printf(" a1=%i\n", a1); printf(" a2=%i\n", a2); for (i=3; i< =n; i++) {          a3=a2+a1;          printf(" a%i=%i \n", i, a3);          if(a2%2==0)               s=s+1;          a1=a2;          a2=a3; } printf(" s=%i \n", s); return 1; }

Примечание. В алгоритме использована рекурсивная формула

 

 

3. Создать проект и реализовать данную задачу в среде                 Visual C++ 6. 0.

Последовательности в примерах 1 и 2 являются возрастающими, поэтому вычисление элементов ограничивается заданием их количества.

Пример 3. Для заданных действительного x и целого n вычислить сумму .

 

Ход выполнения работы

1. Написание алгоритма решения задачи будет состоять из двух шагов.

Формула для вычисления суммы:

.

Здесь  i обозначает номер текущего элемента последовательности, n – количество элементов последовательности, сумму которых нужно вычислить.

Глубина рекурсии в данном случае не определяется, так как данная формула не является рекуррентной.

2. Написать программу, соответствующую алгоритму6

Алгоритм

Программа

Объявление цел: i, n; вещ: х, s, а //ввод количества элементов ввод n ввод x //начальное значение номера элемента //последовательности i=0 //начальное значение элемента // последовательности а=sin(x)/x //начальное значение суммы элементов //последовательности s=a //цикл для вычисления элементов и суммы //последовательности для i=1 до n шаг 1 a= (-1)isini(x)/xi s=s+a всё_для i //вывод полученной суммы на экран печать s

#include " stdio. h" #include " math. h" int main ( ) { int i, n; float x, s, a; printf(" n=" ); scanf(" %i", & n); printf(" x=" ); scanf(" %f", & x); // инициализация переменных i=0; a=sin(x)/x; s=0; //цикл для вычисления элементов и //суммы последовательности for (i=1; i< =n; i++) {          a=pow(-1, i)*pow(sin(x), i)/pow(x, i);          s=s+a; } //вывод полученной суммы на экран printf(" s=%f \n", s); return 1; }

Примечание. В алгоритме использована рекурсивная формула

 

3. Создать проект и реализовать данную задачу в среде                 Visual C++ 6. 0.

Пример 4. Для заданного вещественного х и малой величины eps вычислить сумму ряда .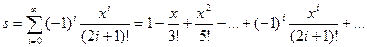

 

Ход выполнения работы

1. Написание алгоритма решения задачи будет состоять из двух шагов.

Рекуррентная формула выводится из предположения, что слагаемые ряда являются членами бесконечно убывающей геометрической прогрессии. Пусть . Таким образом, рекуррентная формула выглядит следующим образом:

,

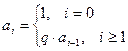где . Формула для  берется из формулы ряда 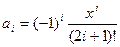. Для нахождения формулы  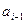подставим в формулу  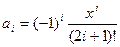i-1 вместо i: .

Для вычисления q необходимо знать, что есть факториал числа. Факториалом числа i называют произведение последовательных натуральных чисел от 1 до i включительно, т. е. i! = 1·2·3·…·(i-1)·i. Следовательно, (2i-1)! = 1·2·3·…·(2i-1), а (2i+1)! = 1·2·3·…·(2i-1)·2i·(2i+1). Вычислим 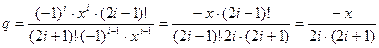. Получим рекуррентную формулу

.

 

При записи этой формулы наиболее частой ошибкой является следующая

запись этой формулы:

.

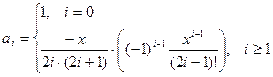Эта формула не будет являться рекуррентной, так как в ней нет зависимости последующего элемента последовательности от предыдущего, следовательно, нет возможности применить стандартный алгоритм вычисления элементов и суммы этих элементов (описание см. ниже).

Глубина рекурсии равна 2, т. е. для вычисления элементов последовательности требуются две переменные. Как и в примере 1, обойдемся одной переменной.

Примечание. При вычислении суммы ряда решающую роль играет величина eps. Она задаётся для того, чтобы ограничивать количество вычисляемых элементов последовательности, добавляемых в сумму. При вычислении каждого элемента последовательности его модуль сравнивается с eps. Если он больше eps, то вычисления продолжаются, в противном случае вычисление элементов последовательности и добавление их в искомую сумму прекращается. Такой процесс называется вычислением суммы ряда с точностью eps. В качестве значения переменной eps можно взять 0, 001 или 0, 00001 и т. п.

2. Написать программу, соответствующую алгоритму:

Алгоритм

Программа

Объявление вещ: х, eps, S, a, цел: i ввод х, eps //начальное значение номера элемента //последовательности i=0 //начальное значение элемента //последовательности a=1 //начальное значение суммы элементов //последовательности s=a //цикл для вычисления элементов и //суммы последовательности покa |a|> =eps //увеличиваем номер элемента   i=i+1 //вычисляем новый элемент   a=a*(-x)/(2*i*(2*i+1)) //добавляем его в сумму   s=s+a все_цикл печать s

#include " stdio. h" #include " math. h" int main ( ) { int i; float x, eps, a, s; printf(" x=" ); scanf(" %f", & x); printf(" eps=" ); scanf(" %f", & eps); // инициализация переменных i=0; a=1; s=a; //цикл для вычисления элементов и //суммы последовательности while (fabs(a)> =eps) {         i=i+1;         a=a*(-x)/(2*i*(2*i+1));         s=s+a; } //вывод полученной суммы на экран printf(" S=%f \n", s); return 1; }

3. Создать проект и реализовать данную задачу в среде                 Visual C++ 6. 0.

Пример 5. Найти наименьший номер члена последовательности, для которого выполняется условие 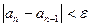. Вывести на экран номер и все элементы 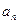, где  . Последовательность задается формулой .

 

Ход выполнения работы

1. Написание алгоритма решения задачи будет состоять из двух шагов.

Формула для вычисления элементов последовательности:

,

где i – номер текущего элемента последовательности.

Глубина рекурсии в данном случае равна 1, т. е. для вычисления элементов последовательности нужны две переменные.

2. Написать программу, соответствующую алгоритму:

Алгоритм

Программа

Объявление цел: i; вещ: аt, ap, eps ввод eps //номер элемента равен 1 i=1 // текущий элемент аt=0. 01 печать at //номер элемента увеличивается на 1 i++ // новый элемент ap=ln2(at)+1 печать ap // цикл для вычисления элементов //последовательности пока |at-ap|> =eps //номер элемента увеличивается на 1 i++   //последующий элемент становится //текущим at=ap //вычисляется последующий элемент ap=ln2(at)+1 печать ap всё_цикл печать i

#include " stdio. h" #include " math. h" int main ( ) { int i; float at, ap, eps; printf(" eps=" ); scanf(" %f", & eps); i=1; at=0. 01; printf(" a%i=%f\n", i, at); i++; ap=pow(log(at), 2)+1; printf(" a%i=%f\n", i, ap); // цикл для вычисления элементов  //последовательности while (fabs(at-ap)> =eps) {          i++;               at=ap;          ap=pow(log(at), 2)+1;          printf(" a%i=%f\n", i, ap); } printf(" min №=%i \n", i); return 1; }

3. Создать проект и реализовать данную задачу в среде                 Visual C++ 6. 0.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: