 |
Тема 7 Арифметические устройства
|
|
|
|
План
Сумматоры
Цифровые компараторы (устройства сравнения)
Арифметико-логическое устройство
Дискретная математика оперирует классом приборов, которые выполняют арифметические действия над двоичными числами: сложение, вычитание, умножение, деление, сравнение.
Особенность арифметических устройств состоит в том, что сигналам присваиваются не логические, а арифметические значения 1 и 0 и действия над ними подчиняются законам двоичной арифметики.
Арифметические устройства выпускаются в виде готовых изделий в составе многих серий цифровых микросхем.
Сумматоры
Студент должен
Знать:
· Назначение сумматоров;
· Классификация сумматоров;
· Принцип работы сумматоров, их параметры.
Уметь:
· По заданным параметрам выбирать по справочнику микросхему сумматора.
Полусумматор
Простейшим суммирующим элементом является полусумматор. Он имеет (рисунок 7.1) два входа А и В для двух слагаемых и два выхода: S (сумма) и P (перенос).

Рисунок 7.1
Обозначением полусумматора служат буквы HS (half sum – полусумма).
Работу полусумматора отображает таблица истинности 7.1.
Таблица 7.1 - Таблица истинности полусумматора
| Входы | Выходы | ||
| А | В | P | S |
| 0 | |||

Два одноразрядных числа при сложении в двоичной системе счисления дают (применительно к суммирующим устройствам) результаты (рисунок 7.2).
Рисунок 7.2
Логическая структура полусумматора такова, что состояние выхода S отображает бит суммы, а выхода P – бит переноса. Это следует и из таблицы истинности полусумматора.
Работа полусумматора описывается следующими уравнениями 

Выражение для выхода S, равно как и столбец S таблицы истинности, полностью совпадает с уравнениями и таблицей истинности для логического элемента «исключающее ИЛИ». Это обстоятельство объясняет, в частности, почему операцию «исключающее ИЛИ» иногда называют сложением по модулю 2.
|
|
|
Логическая структура полусумматора в общем и развернутом виде показана на рисунке 7.3.

Рисунок 7.3
Полный сумматор

Процедуру сложения двух n-разрядных двоичных чисел можно представить следующим образом (рисунок 7.4).
Рисунок 7.4
Сложение цифр А1 и В1 младшего разряда дает бит суммы S1 и бит переноса Р1. В следующем (втором) разряде происходит сложение цифр Р1, А2 и В2, которое формулирует сумму S2 и перенос Р2.
Операция сложения длится, пока не будет сложена каждая пара цифр во всех разрядах. Результатом сложения будет число S = Pn Sn…S1, где Pn и Si отображают 1 или 0, полученные в результате поразрядного сложения.
Полусумматор имеет два входа и пригоден поэтому для использования только в младшем разряде.
Устройство для суммирования двух много разрядных чисел должно иметь, начиная со второго разряда, три входа: два для слагаемых А1 и В1 и один для сигнала переноса Рi-1 с предыдущего разряда.

Этот узел – сумматор можно представить как объединение двух полусумматоров (рисунок 7.5).
Рисунок 7.5
Первый полусумматор служит для сложения двух чисел, принадлежащих одному разряду, и обеспечивает выход промежуточной суммы Si и переноса Рi. Второй полусумматор складывает перенос с предыдущего разряда Pi-1 с промежуточной суммой Si. Функции выходов S и P для этого случая определяются как:
S=(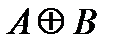 )
)  Pi-1; Pi-1=Ai Bi v (
Pi-1; Pi-1=Ai Bi v (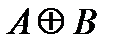 )Pi-1
)Pi-1
Операция сложения подчиняется переместительному закону, из которого следует, что входы сумматора можно менять местами без ущерба для результата.
Исходя из таблицы истинности сумматора 2, можно написать следующие булевы уравнения для сигналов суммы и переноса:
|
|
|

Pi= 
В уравнениях и представлены только те члены, для которых Si=1 и Pi=1, т.е. первый член функции Si относится к первой строке таблицы истинности, второй член ко второй и т.д.. Сходным образом для функции P первый член принадлежит третьей строке, второй член – пятой и так до седьмой.
Уравнения и поддаются минимизации, в результате которой получается

Pi= 
Легко убедиться, что оба уравнения удовлетворяют таблице истинности 7.2.
В микросхемах-сумматорах в качестве базового узла используется сумматор (рисунок 7.6), логическая структура которого реализована на основе формул минимизированных формул.
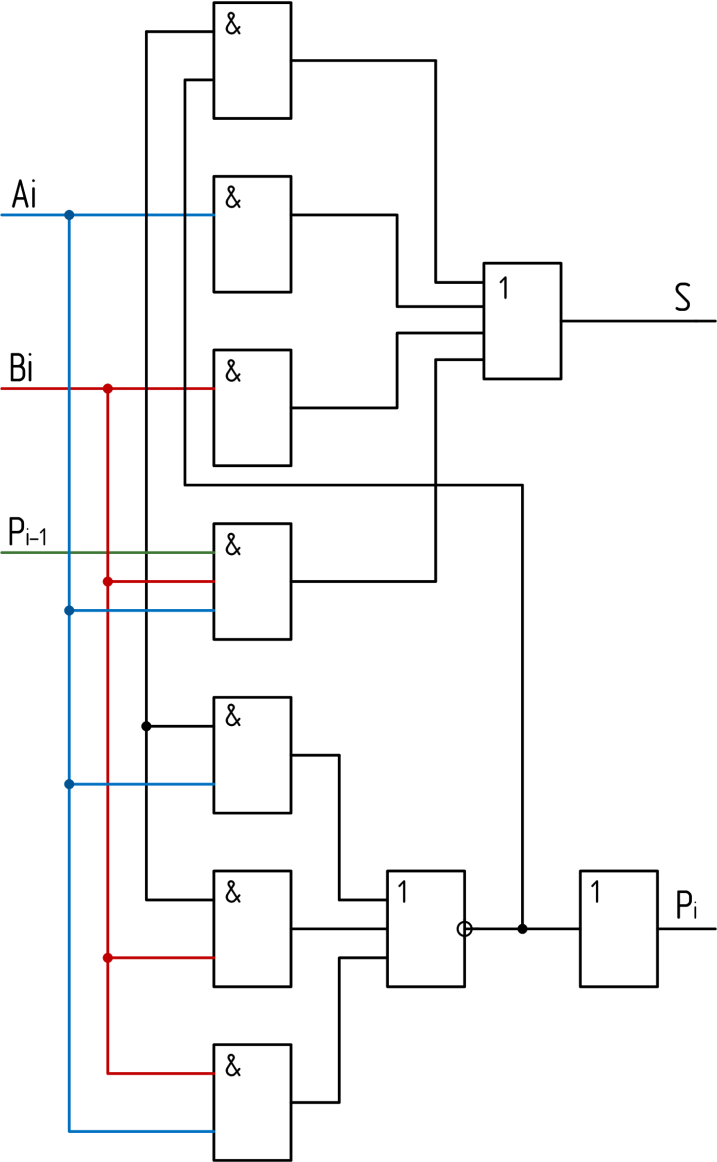
Таблица 7.2 - Таблица истинности полного сумматора
| № п/п | Входы | Выходы | |||
| Ai | Bi | Pi | Pi-1 | Si | |
Рисунок 7.6
|
|
|


