Основные физические свойства газов

Сжимаемость. Свойство газа изменять объем под действием давления называют сжимаемостью. Сжима­емость характеризуется коэффициентом объемного сжатия β, который представляет собой относитель­ное изменение объема, приходящееся на единицу давления:

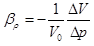
Знак «минус» в формуле обусловлен тем, что положительному приращению (увеличению) давления соот­ветствует отрицательное приращение (уменьшение) объема V. Величина, обратная коэффициенту β, носит название объемного модуля упругости (модуля сжимаемости) К [Па].

Температурное расширение. Температурное расширение характеризуется коэффициентом объемного расширения βт [К1], который представляет собой относительное изменение объема при изменении температу­ры на 1 К:

 

 

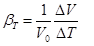
Вязкость. Свойство жидкостей и газов оказывать сопротивление сдвигу (скольжению) слоев жидкости или газа называют вязкостью. Вязкость — свойство противоположное текучести (степениподвижности частиц жидко­сти или газа): более вязкие жидкости менее текучие и наоборот. Вязкость может быть охарактеризована коэффи­циентами динамической вязкости ji и кинематической вязкости v.

Единицей измерения коэффициента динамической вязкости β, или коэффициента внутреннего трения, яв­ляется паскаль-секунда [Па-с]. Используется также единица измерения пуаз [П] системы единиц СГС: 1 П = 0,1 Па-с. Единицей коэффициента кинематической вязкости v служит м² /с; применяют также единицу СГС стоке [Ст]: 1 Ст = 1 с м² /с = 1СИ м² /с.

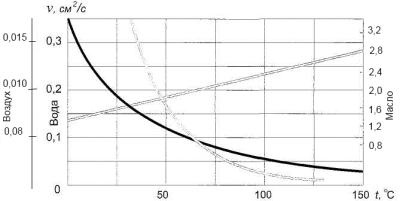
Вязкость зависит от температуры (рис. 2.3), причем характер этой зависимости для жидкостей и газов раз­личен: вязкость жидкостей с увеличением температуры уменьшается, тогда как вязкость газов, наоборот, уве­личивается (для воздуха данная зависимость незначительна).

Рис. 2.3. Зависимость кинематической вязкости v от температуры

Основные газовые законы

 

Состояние газа характеризуется тремя основными параметрами — абсолютным давлением, абсолютной температурой и плотностью (удельным объемом). Взаимосвязь этих параметров газа именуют уравнением состояния. Состояние газа, называемого идеальным, описывается уравнением Клапейрона — Менделеева

Р =pRT,

Где Р —абсолютное давление, Н/ м²;

р — плотность, кг/ м³;

R — удельная газовая постоянная, Дж/ (кг- К); обычно для воздуха R = 287 Дж/ (кг- К); Т—абсолютная температура, К.

Идеальным газом называют такой газ, в котором отсутствуют силы взаимодействия между молекулами, считающимися материальными точками, не имеющими объема. Несмотря на то что воздух не является иде­альным газом, для большинства газовых процессов, протекающих при давлениях, не превышающих 20 МПа (200 бар), это уравнение остается в достаточной мере справедливым.

Введя в данное уравнение формулу, определяющую плотность через массу и объем, получим соотношение, которое описывает состояние m килограммов идеального газа объемом V:

mR=pV/T

Нетрудно заметить, что для какой-либо постоянной массы газа левая часть уравнения есть величина неиз­менная (константа):

pV/T=const

Данное уравнение обобщает основные газовые законы: Бойля — Мариотта, Шарля и Гей-Люссака.

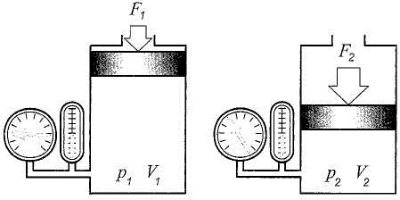
Закон Бойля — Мариотта. Если абсолютная температура газа остается постоянной, то произведение аб­солютного давления газа на его объем есть также величина постоянная для данной массы газа; иными слова­ми, давление газа обратно пропорционально его объему (рис. 2.4).

 

Рис. 2.4. Иллюстрация закона Бойля — Мариотта

Газовые процессы, протекающие при постоянной температуре, называют изотермическими. Если при сжатии газа отсутствует теплообмен с окружающей средой, то такой процесс называют адиабати­ческим (адиабатным). Для него справедливо уравнение Пуассона

р V = const,

где к— коффициент Пуассона, или коэффициент (показатель) адиабаты (для воздуха к — 1,4).

Закон Шарля. Если замкнутый объем данной массы газа остается постоянным, то отношение абсолютного давления газа к его абсолютной температуре есть также величина постоянная; иными словами, давление газа прямо пропорционально его температуре.

Например, при нагревании газа в замкнутом объеме его давление возрастает, а при охлаждении, наоборот, падает (рис. 2.5).

 

Рис. 2.5. Иллюстрация закона Шарля

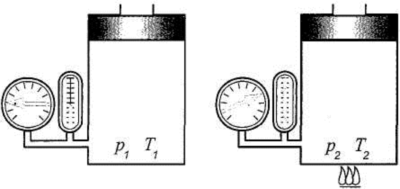
Газовые процессы, протекающие при постоянном объеме, называют изохорическими (изохорными).

Закон Гей-Люссака. Если абсолютное давление газа остается постоянным, то отношение объема данной массы газа к его абсолютной температуре есть также величина постоянная; иными словами, объем прямо пропорционален температуре.

Например, при нагревании газа, находящегося под постоянным давлением, его объем увеличивается, а при охлаждении — уменьшается (рис. 2.6).

 

р = const V1/T1=V2/T2

 

 

Рис. 2.6. Иллюстрация закона Гей-Люссака

 

Газовые процессы, протекающие при постоянном давлении, называют изобарическими (изобарными)*.

Поскольку параметры газа взаимосвязаны и могут изменяться в широком диапазоне значений, то количе­ства газа находящиеся в различных условиях, с целью их сравнения приводят к так называемым нормальным условиям.

Общепринятыми являются следующие параметры нормальных условий:

физические нормальные условия: давление 1,013.105 Па (1,013 бар), температура 273,15 К (0° C);

технические нормальные условия: давление 1,013.105 Па (1,013 бар), температура 293,15 К (20° C).

 

Течение газа

 

Выше мы рассмотрели такие параметры газа, как давление, температура, плотность, удельный объем. Те­чение же газа характеризуется еще одним параметром — расходом.

 

Расход

Расход — величина, определяемая отношением массы (массовый расход) или объема (объемныйрасход) вещества, равномерно перемещаемого через сечение, перпендикулярное направлению скорости потока, к про­межутку времени, за который это перемещение происходит.

В технической литературе объемный расход обозначают латинской буквой Q (или Qv). Определяется объем­ный расход соотношением

Q=V/t

где Q — объемный расход, м³/с; V— объем, м³; t — время, с.

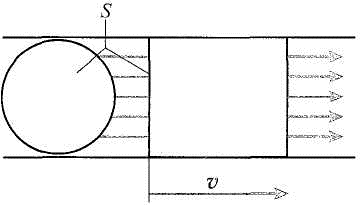
Если речь идет о течении газа, к примеру, по трубопроводу, то объемный расход можно также представить как произведение площади поперечного сечения трубы на среднюю по сечению скорость движения газа в ней (рис. 2.7):

Q =vS,

где v — средняя по сечению скорость потока, м/с;

S — площадь поперечного сечения трубопровода, м².

 

Рис. 2.7. Объемный расход

 

Массовый расход Qm [кг/с], в отличие от объемного, зависит от плотности р [кг/ м³ ] газа и определяется из соотношения

Qm=pvS

Нетрудно заметить, что между объемным и массовым расходами существует следующая зависимость:

Q=Qm/p

В общем случае газ принято рассматривать как сжимаемую вязкую жидкость. Одновременный учет того, что газ представляет собой сжимаемую среду и что при его движении проявляется действие сил трения, значи­тельно затрудняет расчеты. Поэтому на практике во многих случаях прибегают к идеализации процессов дви­жения газа, что упрощает расчеты, не приводя при этом к большим погрешностям.

Чтобы понять суть процессов, происходящих при течении газа, будем рассматривать его как несжимаемую невязкую (идеальную) жидкость.

Исходя из закона сохранения вещества, а также из предположения о сплошности (неразрывности) потока для установившегося течения* несжимаемой жидкости, можно утверждать, что объемный расход через любое сечение одинаков (рис, 2.8).

 

 

Рис. 2.8. Расход жидкости при течении по трубе переменного сечения

 

 

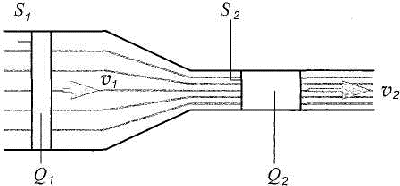
Это явление описывается уравнением неразрывности

Q₁ =S₁v₁ = S₂ v₂ = Q₂ = const.

Из данного уравнения следует, что в узком сечении трубы поток ускоряется:

v₂=v₁S₁/S₂

 

Уравнение Бернулли

Результаты измерений давления в различных точках потока, движущегося по трубе с переменной площа­дью поперечного сечения (рис. 2.9), могут показаться, на первый взгляд, парадоксальными: в узком сечении давление меньше, чем в широком. По каким же причинам имеет место данное явление?

Рис. 2.9. Течение жидкости по трубе переменного сечения

 

 

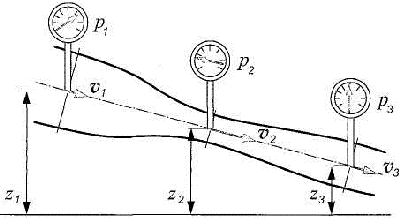
Механическая энергия движущейся жидкости может иметь три формы: энергия положения, энергия давле­ния и кинетическая энергия. В процессе движения идеальной жидкости одна форма энергии может превра­щаться в другую, однако полная удельная энергия жидкости остается неизменной. Математически данное положение описывается уравнением Бернулли

gz₁+p₁/p+v₁²/2=gz₂+p₂/p+v₂²/2= gz₃+p₃/p+v₃²/2

где gz — удельная энергия положения (g — 9,8 м/с² — ускорение свободного падения); p — удельная энергия давления; v²/ 2 — удельная кинетическая энергия.

Таким образом, снижение уровня давления жидкости в узком сечении трубы обусловлено тем, что ускоре­ние потока сопровождается возрастанием его кинетической энергии и, следовательно, уменьшением энергии давления.

В ряде случаев удобно применять форму записи уравнения Бернулли, при которой члены уравнения имеют размерность давления:

gz₁+p₁+v₁²/2=gz₂+p₂+v₂²/2

где pgz — весовое давление;

p — гидромеханическое давление (или просто давление); pv₂/2 — динамическое давление.

В практических расчетах недопустимо пренебрегать потерями энергии по длине трубопровода, а также на местных сопротивлениях. Все реальные жидкости и газы имеют вязкость, и поэтому энергия потока жидкости или газа будет убывать от сечения к сечению по направлению его движения. Потери энергии определяются многими факторами: площадью поперечного сечения и длиной трубопровода, шероховатостью его внутренней поверхности, наличием местных сопротивлений, скоростью и режимом течения, вязкостью (внутренним трени­ем) жидкости или газа.

Уравнение Бернулли для потока реальной (вязкой) жидкости в энергетической форме будет иметь следую­щий вид:

gz₁+p₁/p+α₁v₁²/2= gz₂+p₂/p+α₂v₂²/2+gΣhn

где α — коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению

потока; g Σhn — суммарные потери энергии (гидравлические потери).

Уравнение Бернулли применимо к потоку сжатого воздуха при условии, что скорость его движения v<υ, где υ — скорость звука.

 

Режимы течения

Существует два режима течения жидкостей и газов по трубе: ламинарный и турбулентный (рис. 2.10).

 

Рис. 2.10

Ламинарный режим

Турбулентный режим

 

 

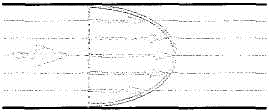
Ламинарный режим характеризуется упорядоченным движением (слоями) жидкости или газа, причем скоро­сти внешних слоев меньше, чем внутренних. Когда скорость движения превысит некоторую критическую вели­чину, слои начинают перемешиваться, образуются вихри; течение становится турбулентным, возрастают поте­ри энергии.

При течении жидкости по трубопроводу переход от ламинарного режима к турбулентному наблюдается в тот момент, когда осредненная по сечению трубы скорость движения потока становится равной критической V_K.

Как показывает эксперимент, критическая скорость прямо пропорциональна кинематической вязкости v жидко­сти и обратно пропорциональна внутреннему диаметру Отрубы:

Vкр=kv/d

где к — коэффициент пропорциональности; v — кинематическая вязкость жидкости, м² /с; d— внутренний диаметр трубы, м.

Экспериментально был также подтвержден тот факт, что смена режима течения любой жидкости или газа по трубе любого диаметра имеет место лишь при определенном значении безразмерного коэффициента к. Данный коэффициент называют критическим числом Рейнольдса:

Reкр= Vкрd/v

Для труб круглого сечения ReK ~ 2300.

Число Рейнольдса используют для описания режима течения:

Re= Vd/v=vpd/μ

Значение числа Рейнольдса позволяет судить о характере течения жидкости по трубе: при Re<ReKp наблю­дается ламинарный режим, при Re>ReKp — турбулентный.

Таким образом, зная скорость движения потока, вязкость жидкости и внутренний диаметр трубы, можно рас­четным путем найти число Рейнольдса и, сравнив его с величиной ReKp, определить режим течения жидкости.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: