 |
Оценка точности геодезических измерений
|
|
|
|
Измерения подразделяются на прямые и косвенные, однократные и многократные, равноточные и неравноточные.
При прямых измерениях значение искомой величины получается непосредственно по показаниям прибора (например, рулеткой измеряется длина отрезка).
При косвенных измерениях значение искомой величины находится вычислениями по известным формулам на основании данных прямых измерений (например, определение площади треугольника по измеренным основанию и высоте).
Однократные измерения дают одно значение измеряемой величины. При многократных – величина измеряется n > 1 раз. Такие измерения необходимы для контроля, позволяют получить более надежный результат.
Равноточные – измерения выполняются в одинаковых условиях: приборами одинаковой точности, исполнителями одинаковой квалификации, одними и теми же методами и равное число раз, при одинаковых условиях внешней среды.
Неравноточные – измерения, выполненные в неодинаковых условиях и поэтому имеющие разную точность.
Любое измерение сопровождается погрешностями измерения, которые разделяют на грубые, систематические и случайные.
Грубые погрешности (ошибки, промахи, просчеты) выявляют и устраняют контрольными измерениями.
Систематические погрешности искажают результат измерений всегда в какую-либо сторону. Например, мерная лента на величину D l короче эталона, или известна ее длина при одной температуре, а измерения производятся при другой, и тогда появится систематическая погрешность за счет теплового линейного расширения материала ленты. Систематические погрешности стараются исключить введением поправок.
Случайные погрешности принципиально неустранимы, так как они изменяются случайным образом при повторных измерениях одной и той же величины. Борьба за уменьшение их влияния сводится к совершенствованию приборов и методов измерений, в частности к увеличению числа повторных измерений, к выбору наиболее благоприятных условий работы
|
|
|
Установлены следующие статистические свойства случайных погрешностей.
1. Погрешности по модулю не превосходят некоторого предела
. (4.1)
2. Равные по модулю положительные и отрицательные погрешности одинаково возможны.
3. Малые погрешности встречаются чаще, чем большие.
4. Среднее арифметическое из погрешностей равноточных измерений стремится к нулю при неограниченном возрастании числа измерений
. (4.2)
На этих свойствах основана оценка погрешностей и установление наиболее достоверных результатов измерений. Надежную оценку точности измерений – среднюю квадратическую погрешность отдельного измерения – предложил Гаусс:
. (4.3)
В большинстве случаев критерий Гаусса обеспечивает более надежную оценку точности по сравнению со средним арифметическим из абсолютных значений погрешностей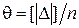 
, что можно видеть из следующего примера.
Пример 1. Пусть имеется два ряда измерений при условии, что точность первого ряда заведомо ниже, так как он содержит более значительные по величине погрешности (–6 и +7).
I ряд: –1; +2; –6; +7; –1 
.
II ряд: –4; +2; –4; +3; –4 .
Тогда 
и 
, то есть получается, что точность обоих рядов одинакова. Но при оценке точности критериев Гаусса получаем
;
.
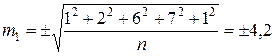Видно, что 
, и наличие в первом ряду больших погрешностей проявилось.
Доказано, что при достаточно большом числе измерений случайная погрешность может быть больше 2 m в пяти случаях из ста и больше 3 m в трех случаях из 1000. Обычно принимают для более ответственных измерений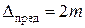 
, отбраковывая те результаты измерений, где погрешность больше 2 m.
Средняя q, средняя квадратическая m и предельная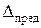 
погрешности называют абсолютными. Они имеют ту же размерность, что и измеряемая величина.
|
|
|
Часто на практике необходимо знать не абсолютную, а относительную погрешность. Например, если одна линия измерена с точностью 
(т.е. на 2000 м погрешность составляет 1 м), а вторая с точностью 
, то, очевидно, что вторая линия измерена точнее. Относительную погрешность обычно представляют дробью, числитель которой равен 1, а знаменатель есть частное от деления измеренной величины на абсолютную погрешность. Так, относительная средняя квадратическая погрешность будет 
. Необходимость оценивать точность измерений возникает в следующих случаях.
1. Истинное значение измеряемой величины X известно заранее, например сумма углов многоугольника. Тогда значение погрешности измерений 
и . В практике такой случай встречается редко.
2. Истинное значение измеряемой величины заранее неизвестно. Тогда, по результатам нескольких равноточных измерений, можно определить наиболее вероятное (вероятнейшее) значение измеряемой величины 
, которым оказывается арифметическое среднее. Зная , можно вычислить вероятные погрешности (отклонения) 
и по формуле Бесселя среднюю квадратическую погрешность отдельного измерения 
.
Но само вероятнейшее значение будет определено также с погрешностью, которую находят по формуле 
.
Пример 2. Даны результаты измерения линии (табл. 4.1). Оценить точность измерений, т.е. вычислить m, M и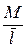 
.
Т а б л и ц а 4.1
Исходные данные
| Номер измерения | l, м | V, см | v 2, см2 |
| 68,31 | –1 | ||
| 68,30 | –2 | ||
| 68,34 | +2 | ||
| 68,32 | |||
| 68,33 | +1 | ||
| 
| 
|
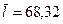
Решение
м.
см.
см.
.
3. Измеряемая величина определяется косвенным путем, то есть является функцией 
других измеренных с какой-то точностью величин (так называемых измеряемых аргументов), средние квадратические погрешности которых mx; my; … mt.
В теории погрешностей измерений доказано, что средняя квадратическая погрешность величины 
выражается следующей формулой
(4.4)
Пример 3. В треугольнике на плане измерено основание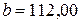 
м с 
см и высота 
м с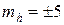 
см. Определить относительную среднюю квадратическую погрешность площади треугольника 
.
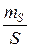Площадь треугольника участка равна
|
|
|
м2.
Найдем частные производные от функции S по аргументам b и h.
; 
.
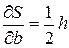Тогда
м2
и
.
Сведения, приведенные в данном пособии, являются дополнением к основным темам, изучаемым на лекциях. Они позволяют студентам получить практические навыки в решении конкретных инженерных задач.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Топографические съемки и разбивочные работы: Метод. указ. по учебной геодезической практике / Сост. С.В. Гладышев, В.С. Ермаков. Л.: ЛПИ. 1989. 44 с.
2. Инженерная геодезия. Геодезическое обеспечение строительства и эксплуатации морских и воднотранспортных сооружений: Учеб. пособие /
В.С. Ермаков, Н.Н. Загрядская, Е.Б. Михаленко, Н.Д. Беляев. СПб.: Изд-во СПбГТУ, 2001. 71 с.
3. Инженерная геодезия. Геодезические разбивочные работы: Учеб. пособие / Е.Б. Михаленко, Н.Д. Беляев, В.В. Вилькевич, Н.Н. Загрядская, А.А. Смирнов. СПб.: Изд-во Политехн. ун-та, 2004. 50 с.
4. Инженерная геодезия. Решение основных инженерных задач на планах и картах: Учеб. пособие / Е.Б. Михаленко, Н.Н. Загрядская, Н.Д. Беляев и др. СПб.: Изд-во Политехн. ун-та, 2006. 105 с.
5. Аболин Е.Р., Ершов А.В., Тихонюк Н.К., Шинкевич В.А. Пособие по геодезическому обеспечению строительства. СПБ., 2006. 240 с.
ОГЛАВЛЕНИЕ
| 1. Геодезические разбивочные работы............................. | |||
| 1.1. Строительная сетка...................................... | |||
| 1.2. Содержание и основные этапы выполнения геодезических разбивочных работ.......................................... | |||
| 1.3. Подготовка данных для разбивочных работ.................. | |||
| 1.4. Расчет разбивочных элементов для перенесения проектной линии в натуру............................................. | |||
| 1.4.1. Вычисление исходных данных....................... | |||
| 1.4.2. Составление разбивочного чертежа................... | |||
| 1.5. Основные элементы плановых разбивочных работ............ | |||
| 1.5.1. Построение линий заданной длины................... | |||
| 1.5.2. Построение горизонтального угла проектной величины.. | |||
| 1.5.3. Построение линии проектной длины в заданном направлении........................................... | |||
| 1.5.4. Построение заданного направления вне пункта разбивочной сети........................................ | |||
| 1.6. Вынос в натуру планового положения точек сооружения...... | |||
| 1.6.1. Способ прямоугольных координат.................... | |||
| 1.6.2. Способ прямой угловой засечки...................... | |||
| 1.6.3. Способ полярных координат......................... | |||
| 1.6.4. Способ линейной засечки........................... | |||
| 1.6.5. Способ проектного полигона....................... | |||
| 1.7. Основные элементы высотных разбивочных работ............ | |||
| 1.7.1. Вынос точек с проектными отметками................ | |||
| 1.7.2. Вынос на местность линий с проектными уклонами..... | |||
| 1.7.3. Вынос в натуру плоскостей с заданными уклонами...... | |||
| 1.8. Детальные разбивочные работы по выносу осей и отметок.... | |||
| 1.8.1. Разбивка и закрепление осей сооружения на обноске.... | |||
| 1.8.2. Разбивочные работы на исходном монтажном горизонте. | |||
| 1.8.3. Передача осей на монтажные горизонты............... | |||
| 1.8.4. Передача отметок на монтажные горизонты............ | |||
| 2. Геодезические исполнительные съемки......................... | |||
| 2.1. Система исполнительских съемок в строительстве............ | |||
| 2.2. Типовые геодезические исполнительные схемы.............. | |||
| 3. Геодезические наблюдения за деформациями сооружений......... | |||
| 3.1. Общие принципы и методы проведения геодезических наблюдений................................................ | |||
| 3.2. Геодезические наблюдения за морскими сооружениями....... | |||
| 3.3. Наблюдения за креном сооружений........................ | |||
| 3.3.1. Определение крена сооружений башенного типа........ | |||
| 3.3.2. Решение некоторых инженерных задач, связанных с определением крена..................................... | |||
| Определение неприступного расстояния............... | |||
| Определение высоты сооружения..................... | |||
| 4. Оценка точности геодезических измерений...................... | |||
| Библиографический список...................................... |
|
|
|
МИХАЛЕНКО Евгений Борисович
ЗАГРЯДСКАЯ Наталия Николаевна
БЕЛЯЕВ Николай Дмитриевич
Вилькевич Валентин Войтехович
ДУХОВСКОЙ Федор Николаевич
СМИРНОВ Александр Александрович
ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
|
|
|
