 |
Наиболее распространенным является аналитический способ задания функции, при котором указывается формула, задающая алгоритм вычисления значений функции для любого значения аргумента.
|
|
|
|
ОСНОВНЫЕ ТЕРМИНЫ И ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ ИССЛЕДОВАНИИ ФУНКЦИИ
С ПОМОЩЬЮ ЕЕ ПРОИЗВОДНЫХ
1. Числовой функцией одного аргумента (одной переменной) 
называется такое соответствие между двумя числовыми множествами, при котором для любого значения одной независимой переменной х из множества D находится строго определенное единственное значение переменной y из множества E.
2. Областью определения функции Dназывается множество значений аргумента, для которых формула задающая функцию имеет смысл; множество всех возможных значений функции Е называется областью значений функции.
Наиболее распространенным является аналитический способ задания функции, при котором указывается формула, задающая алгоритм вычисления значений функции для любого значения аргумента.
Функция может быть задана в явном виде, т.е. уравнением , или в неявном виде, т.е. уравнением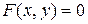 
, которое иногда можно разрешить относительно переменной 
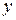и выразить функцию в явном виде.
Например, функции 
, 
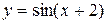- явные функции; функции 
, 
- неявные, причем из первой функции можно выразить переменную 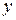в явном виде: 
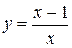, а из второй - нельзя.
4. Графиком функции называется геометрическое место точек плоскости xOy, координаты которых удовлетворяют уравнению .
5. Функция называется четной, если для любого значения х выполняется равенство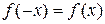 
. График четной функции симметричен относительно оси ординат.
Функция называется нечетной, если для любого значения х выполняется равенство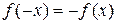 
. График нечетной функции симметричен относительно начала координат.
6. Функция называется периодической, если существует такое положительное число Т, называемое периодом функции, для которого при любом значении числа х выполняется равенство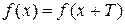 
.
|
|
|
Обычно на периодичность проверяют функции, в которые входят тригонометрические зависимости.
7. Асимптотой кривой линии называется прямая линия, если расстояние от кривой до этой прямой стремится к нулю при неограниченном удалении кривой от начала координат (т.е. при стремлении хотя бы одной из координат к бесконечности).
Вертикальной асимптотой кривой является прямая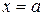 
, ес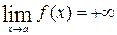ли 
или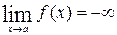 
.
Горизонтальной асимптотой кривой является прямая 
, если существует предел 
или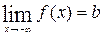 
.
Наклонной асимптотой кривой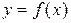 
является прямая 
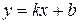, если существуют пределы 
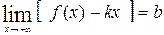или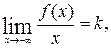 
.
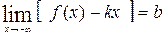8. Функция называется возрастающей в интервале (a; b), если для любых двух точек х1 и х2 из этого интервала, удовлетворяющих условию х1 < х2, выполняется неравенство 
.
Функция называется убывающей в интервале (a; b), если для любых двух точек х1 и х2 из этого интервала, удовлетворяющих условию х1 > х2, выполняется неравенство 
.
Признаки возрастания и убывания функции: если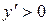 
на интервале (a, b), то функция 
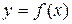возрастает на этом интервале; если 
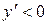на интервале (a, b), то функция убывает на этом интервале.
9. Экстремумом функции называется максимальное или минимальное значение функции при изменении ее монотонности, т.е. при переходе между промежутками возрастания и убывания.
Точки, в 
которых производная равна нулю или не существует, называются критическими на экстремум. В этих точках функция может иметь экстремум. Если у ¢ существует всюду в области определения функции, следовательно, критические точки найдем из уравнения у ¢ = 0.
Для проверки критических точек на экстремум используем достаточное условие существования экстремума: если функция определена и непрерывна в точке х0 и ее окрестности, дифференцируема в окрестности точки х0, и ее производная при переходе через точку х0 меняет знак, то х0 - точка экстремума; при смене знак производной с “ + “ на “ - “ х0 - точка локального максимума, при смене знака производной с “ - “ на “ + “ х0 - точка локального минимума.
|
|
|
Значение экстремума находятся подстановкой значений точек экстремума в формулу, задающую функцию: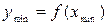 
; 
.
10. График функции называется выпуклым в интервале (a; b), если он расположен ниже касательной, проведенной к кривой в любой точке этого интервала.
График функции называется вогнутым в интервале (a; b), если он расположен выше касательной, проведенной к кривой в любой точке этого интервала.
При исследовании графика функции на выпуклость, вогнутость и точки перегиба пользуемся правилом: если у ² < 0 в интервале (а; в), то график функции на этом интервале выпуклый, если у ² > 0 в интервале (а; в), то график вогнутый.
11. Точка (х0; f (х0 )), лежащая на графике функции и отделяющая его выпуклую часть от выгнутой, называется точкой перегиба.
Точки, в которых вторая производная равна нулю или не существует, называются критическими на перегиб. В этих точках функция может иметь экстремум, у ¢¢ существует всюду в области определения функции, следовательно, критические точки найдем из уравнения у ¢¢ = 0
Для проверки критических точек на перегиб используем достаточное условие существования перегиба: если функция определена и непрерывна в точке х0 и ее окрестности, дважды дифференцируема в окрестности точки х0, и ее вторая производная при переходе через точку х0 меняет знак, то х0 - точка перегиба.
Значение перегиба находятся подстановкой значений точек экстремума в формулу, задающую функцию: 
.
ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ
И ПОСТРОЕНИЯ ЕЕ ГРАФИКА
| 1 | Записать функцию в явном виде |
| 2 | Найти область определения функции |
| 3 | Проверить функцию на четность и нечетность |
| 4 | Проверить функцию на периодичность |
| 5 | Найти точки пересечения графика функции с осями координат |
| 6 | Найти асимптоты графика функции |
| 7 | Найти первую производную функции и точки, критические на экстремум |
| 8 | Определить промежутки монотонности функции |
| 9 | Найти экстремумы функции |
| 10 | Найти вторую производную функции и точки, критические на перегиб |
| 11 | Определить промежутки выпуклости и вогнутости графика функции |
| 12 | Найти точки перегиба графика функции |
| 13 | Построить график функции |
|
|
|
|
|
|
