 |
Пример исследования функции
|
|
|
|
Исследовать функцию  и построить ее график.
и построить ее график.
Выразим функцию в явном виде.
В левой части формулы содержится переменная величина y в первой степени, а в правой – только другая переменная х, поэтому функция задана в явном виде.
Найдем область определения функции.
Функция определена всюду, кроме точки х = 1, т. к. знаменатель дроби при х = 1 обращается в нуль.
Значит, D (х) = (- ¥; 1) È (1; + ¥), а х = 1 – точка разрыва.
Проверим функцию на четность или нечетность.
Так как функция имеет одну точку разрыва, которая не совпадает с началом координат, т. е. область определения функции не симметрична относительно точки х = 0, то говорить о четности или нечетности не имеет смысла, тем не менее проведем проверку по общему правилу:
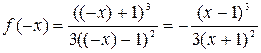 = -
= - 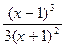 ,
,
т.е. f (- х) ¹ f (х) и f (- х) ¹ - f (х) - рассматриваемая функция не является четной и не является нечетной, это функция общего вида.
Проверим функцию на периодичность.
Не существует такого числа Т, для которого бы выполнялось условие:
f (х) = f (х + Т), т. е. функция не является периодической.
Найдем точки пересечения графика функции с осями координат.
При х = 0 у (0) = 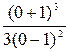 =
= 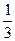 , значит точка с координатами (0;
, значит точка с координатами (0; 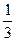 ) – точка пересечения графика функции с осью ординат;
) – точка пересечения графика функции с осью ординат;
если у = 0, то 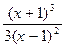 = 0
= 0 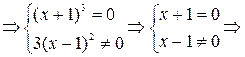 х = -1, значит точка с координатами (-1; 0) – точка пересечения графика функции с осью абсцисс.
х = -1, значит точка с координатами (-1; 0) – точка пересечения графика функции с осью абсцисс.
Найдем асимптоты графика.
· Вертикальная асимптота может быть в точке разрыва х = 1.
Найдем односторонние пределы функции в этой точке:
Предел функции, когда аргумент стремится к точке разрыва слева 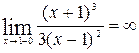 .
.
Предел функции, когда аргумент стремится к точке разрыва справа 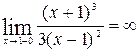 .
.
Значит, вертикальная асимптота у графика функции одна и определяется уравнением х = 1.
|
|
|
· Горизонтальных асимптот график функции не имеет, так как
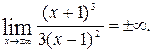
· Наклонные асимптоты.
Находим коэффициенты для записи уравнения наклонной асимптоты  :
:
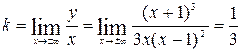
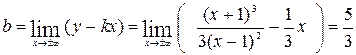 .
.
Наклонная асимптота одна и задается уравнением  .
.
Асимптота пересекает график функции в точке 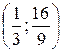 , так как система
, так как система  имеет решение
имеет решение 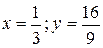 .
.
Найдем первую производную функции.
у¢ = 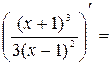

Критические точки найдем из уравнения 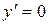 .
.
Имеем:  = 0;
= 0; 
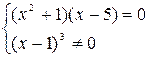


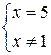

 критическая точка х = 5.
критическая точка х = 5.



Найдем промежутки монотонности.
Разобъем область определения функции на интервалы критическими точками и проверим знак производной в каждом из этих интервалов.
| Х | (- ¥; 1) | (1; 5) | 5 | (5; + ¥) |
| У ¢ | + | - | 0 | + |
| У | | ¯ | Min 4,5 | |
(В таблице стрелка означает возрастание, ¯ - убывание функции.)
Итак, (- ¥; 1) и (5; + ¥) - интервалы возрастания функции;
(1; 5) - интервал убывания функции.
Производная функции при переходе через точку х = 5 меняет знак, с “ - “ на “ + “, значит х = 5 - точка локального минимума.
Найдем значение экстремума.
Значение экстремума находятся подстановкой значений точек экстремума в формулу, задающую функцию, т.е.
ymin = y (5) = 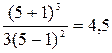 - экстремум (минимум) функции.
- экстремум (минимум) функции.
Найдем вторую производную функции.
у² = (у ¢)¢ = 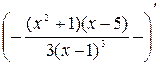 =
= 
Очевидно, что у² существует всюду в области определения функции, поэтому точки, критические на перегиб найдем из условия у² = 0:



 критическая точка х = - 1.
критическая точка х = - 1.
Исследуем график функции на выпуклость, вогнутость и точки перегиба.
Разобъем область определения функции на интервалы критическими точками.
| Х | (- ¥; - 1) | -1 | (-1; 1) | (1; + ¥) |
| У ¢¢ | - | 0 | + | + |
| У | Ç | 0 перегиб | È | È |
Интервалы вогнутости (-1; 1) и (1; + ¥);
|
|
|
интервал выпуклости (- ¥; - 1).
В точке х = -1 вторая производная меняет знак, следовательно - это точка перегиба.
Найдем перегиб графика функции.
Значение перегиба находится подстановкой значения точки перегиба в формулу, задающую функцию, т.е.
у (- 1) = 
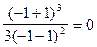 , значит (-1; 0) – точка перегиба графика функции.
, значит (-1; 0) – точка перегиба графика функции.
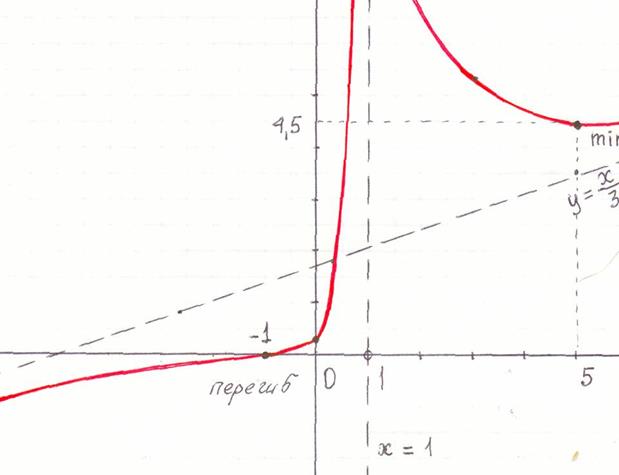
Строим график функции.
Проведя все исследования, строим оси координат, асимптоты, отмечаем все характерные точки (точки экстремума, точки перегиба, точки пересечения с осями координат) и строим график функции.
Если целесообразно уточнение поведения графика функции, то можно вычислить некоторые дополнительные (вспомогательные) точки, например в данном случае целесообразно уточнить прохождение графика функции правее вертикальной асимптоты, т.к.:
y (3) = 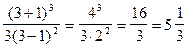 ;
;
y (7) = 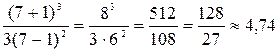
| Вариант | Задание: исследовать функцию и построить ее график | Вариант | Задание: исследовать функцию и построить ее график |

| 
| ||

| 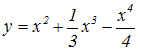
| ||
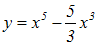
| 
| ||
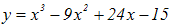
| 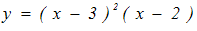
| ||
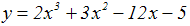
| 
| ||
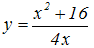
| 
| ||
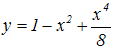
|  
|
|
|
|


