 |
Методы выявления тренда развития социально-экономических процессов.
|
|
|
|
Методы выявления тренда развития социально-экономических процессов.
Тренд – плавноменяющаяся компонента описывающая чистое влияние долговременных факторов.
Тренд - направление преимущественного движения показателей. Обычно рассматривается в рамках технического анализа, где подразумевают направленность движения цен или значений индексов. Выделяют тренды восходящий (бычий), нисходящий (медвежий) и боковой (флэт). На графике часто рисуют линию тренда, которая на восходящем тренде соединяет две или более впадины цены (линия находится под графиком), а на нисходящем тренде соединяет два или более пика цены (линия находится над графиком цен).
Аналитические показатели изменения уровней ряда динамики
Для характеристики интенсивности развития во времени используются статистические показатели, получаемые сравнением уровней между собой, в результате чего получаем систему абсолютных и относительных показателей динамики: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение 1% прироста. Для характеристики интенсивности развития за длительный период рассчитываются средние показатели: средний уровень ряда, средний абсолютный прирост, средний коэффициент роста, средний темп роста, средний темп прироста, среднее абсолютное значение 1% прироста.
Если в ходе исследования необходимо сравнить несколько последовательных уровней, то можно получить или сравнение с постоянной базой (базисные показатели), или сравнение с переменной базой (цепные показатели).
Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.
|
|
|
Абсолютный прирост (базисный)
где yi - уровень сравниваемого периода; y0 - уровень базисного периода.
Абсолютный прирост с переменной базой (цепной), который называют скоростью роста:
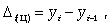
где yi - уровень сравниваемого периода; yi-1 - уровень предшествующего периода.
Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.
Коэффициент роста базисный:
Коэффициент роста цепной:
Темп роста:
Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.
Темп прироста базисный:
Темп прироста цепной:
Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей):
1) Тп = Тр - 100%; 2) Тп = Ki - 1.
Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. Можно выделить две категории показателей в этой группе: а) средние уровни ряда; б) средние показатели изменения уровней ряда.
Средние уровни ряда рассчитываются в зависимости от вида временного ряда.
Для интервального ряда динамики абсолютных показателей средний уровень ряда рассчитывается по формуле простой средней арифметической:
где n - число уровней ряда.
Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической:
где n - число дат.
Средний уровень моментного ряда с неравными интервалами рассчитывается по формуле средней арифметической взвешенной, где в качестве весов берется продолжительность промежутков времени между временными моментами изменений в уровнях динамического ряда:
где t - продолжительность периода (дни, месяцы), в течение которого уровень не изменялся.
|
|
|
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:
Средний темп прироста 
, %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%.
Среднее абсолютное значение 1% прироста можно рассчитать по формуле
Краткое содержание методов (графический метод, скользящей средней, аналитическое выравнивание, модели сезонных колебаний)
Способы построения графиков различны для интервальных и дискретных рядов.
График дискретного ряда распределения можно так же построить следующим образом. На оси абсцисс в одинаковом масштабе откладываются слева направо в порядке возрастания значения вариант данного ряда. По оси ординат наносится шкала для значений величин частот. Из точек на оси Х абсцисс, соответствующих значению исходной варианты, восстанавливаются перпендикуляры (ординаты), причем длина ординаты (высота перпендикуляра) измеряется в единицах масштаба оси ординат. Вершины этих перпендикуляров соединяются в последовательном порядке отрезками прямой. К полученной ломанной линии присоединяются два крайних перпендикуляра.
Полученный график (полигон) четко отражает характер рассматриваемого распределения.
Скользящая средняя - метод сглаживания ценовых показателей, накопленных за некоторый период, называемый порядком скользящего среднего. Скользящее среднее не предназначено для прогнозирования движений на рынке, оно сигнализирует о начале новой тенденции только после ее появления. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом: 
Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.
|
|
|
Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:
1) используя полусумму уровней, расположенных рядом с интерполируемыми;
2) по среднему абсолютному приросту;
3) по темпу роста.
При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле
Под сезонными колебаниями понимается более или менее устойчивые внутригодовые колебания уровней динамического рода, обусловленные спецификами развития данного явления.
При статистическом исследовании в рядах динамики сезонных колебаний решаются следующие взаимосвязанные задачи: 1) выявление специфики развития изучаемого явления во внутренне годовой динамике; 2) измерение сезонных колебаний изучаемого явления с построением модели сезонной волны.
Особое внимание отражается на обеспечение сопоставимости уровней ряда. При наличии в исходном материале разновесных по продолжительности периодов времени объёмные величины пересчитываются в средние величины, характеризующие интенсивность развития изучаемого явления в единицу времени.
Для измерения сезонных колебаний исчисляются специальные статистические показатели, которые называются индексами сезонности и совокупность которых отражает сезонную волну.
Методы прогнозирования развития социально-экономических процессов: регрессионный анализ, метод экстраполяции
Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, т.е. прогноз основан на экстраполяции.
|
|
|
Экстраполяцию следует рассматривать как начальную стадию построения окончательных прогнозов.
Поскольку анализируемые социально-экономические ряды динамики нередко относительно короткие, то горизонт экстраполяции должен быть краткосрочным. Поэтому, чем короче срок экстраполяции, тем более надежные и точные результаты дает прогноз.
Экстраполяцию в общем виде можно представить зависимостью:
где — 
прогнозируемый уровень;
yi — текущий уровень прогнозируемого ряда;
Т — срок экстраполяции;
aj — параметр уравнения тренда.
В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяются следующие простейшие методы экстраполяции:
-среднего абсолютного прироста;
-среднего темпа роста;
-на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему темпу роста осуществляется в случае, когда установлено, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции:
где yi — последний уровень ряда динамики;
t — срок прогноза;
— средний коэффициент роста.
3. 2)Страховые отношения: сущность и классификация. Характеристика страховых отношений. Участники регулируемых страховых отношений. Классификация страхования как система деления страховых отношений на отрасли, подотрасли, виды страхования, формы и системы страховых отношений.
|
|
|
