 |
Развитие алгебры в Европе.
|
|
|
|
Каково же было состояние математики в это время в Европе. Об этом наука располагает крайне скудными сведениями.
В XII – XIII вв. в Европе интенсивно переводились в арабского языка как труды самих арабов, так и работы древних греков, переведенные на арабский язык.
Первым европейским математиком, которому удалось осветить многие вопросы и внести в математику свой вклад, был Леонардо Пизанский (Фибоначчи, 1180–1240), написавший «Книгу абака». В ней рассмотрены различные задачи, указаны методы их решения, причем арифметика и алгебра линейных и квадратных уравнений изложены с небывалой до этого времени точностью и полнотой.
Существо задачи Леонардо излагает словесно; неизвестную он называет res (вещь) или radix (корень); квадрат неизвестной – census (имущество) или quadratus (квадрат); данное число – numerus. Все это латинские пероводы соответствующих латинских слов.
Современник Леонардо, Иордан Неморарий (XIII в), употреблял буквенные обозначения более систематично и решал задачи с применением линейных и квадратных уравнений, сначала в общем виде, а затем иллюстрировал их числовыми примерами.
Французский епископ Николь Орем (1323-1382) рассматривал «дробно – рациональные отношения», соответствующе современным степеням a½, a¼, a3/2 и т.д., сформулировал правила операций с этими отношениями типа  ,
,  ,
,  ,
,  ,
, 
Орем вплотную подошел к понятию иррационального показателя. Он доказал расходимость гармонического ряда 1 +  +
+  +
+  +…
+…
Выдающимся алгебраистом своего времени стал монах-францисканец Лука Пачоли (ок. 1445 – ок.1514) близкий друг Леонардо да Винчи, работавший профессором Математики в университетах и различных учебных заведениях Рима, Болоньи, Неаполя, Флоренции, Милана и других городов.
|
|
|
Он ввел «алгебраические буквы» (caratteri algebraici), дал обозначения квадратному и кубическому корням, корню четвертой степени; неизвестную х он обозначал со (cosa – вещь), х2 – се (censo - квадрат, от латинского census), х3 – cu (cubo), x4 – се. се. (censo de censo), x5 – р°г° (primo relato – «первое relato», x6 – р°г° х – се. cu. (censo de «второе relato»), х8 – ce. ce. ce. (de censo), x9 – cu. cu. (cubo de cubo), x10 – ce. p°r° (censo de primo relato), x13 – 3°r° (tersio relato - «третье relato») и т. д.; свободный член уравнения – n° (numero – число). Как видим, некоторые степени Пачоли получал мультипликативным способом с помощью показателей 2 и 3 (х4 = х2×2 , х6 = х2×3, х9 = х3×3 и т. д.), а в случаях, когда так не получалось, пользовался словом relato (например, при образовании х5, х7, х11 и т. д.). Специальными символами Пачоли обозначил вторую неизвестную и ее степени. Для обозначения операции сложения он воспользовался знаком  (plus – больше), для обозначения вычитания – знаком
(plus – больше), для обозначения вычитания – знаком 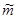 (minus – меньше). Он сформулировал правила умножения чисел, перед которыми стоят знаки
(minus – меньше). Он сформулировал правила умножения чисел, перед которыми стоят знаки  и
и 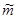 .
.
Раздел «Суммы», посвященный алгебраическим уравнениям, Пачоли закончил замечанием о том, что для решения кубических уравнений х3 + ах = b и х3 + b = ах «искусство алгебры еще не дало способа, как не дан еще способ квадратуры круга».
Некоторый шаг в совершенствовании алгебраической символики сделал бакалавр медицины Н. Шюке (ум. ок. 1500 г.), который в книге «Наука о числах в трех частях» изложил правила действий с рациональными и иррациональными числами и теорию уравнений. Для сложения и вычитания он вслед за Пачоли пользовался знаками  и
и  , причем, знак
, причем, знак  служил и для обозначения отрицательного числа. Неизвестную величину он называл premier («первое число»), а ее степени – вторыми, третьими и т. д, числами. Записи степеней неизвестной у Шюке лаконичны. Например, современные символы 5, 5ж, 5х, 5х2, 5х3 у него выглядели бы так: 5°, 51, 52, 53. Вместо равенства 8х3×7х-1 = 56х2 Шюке писал: «83, умноженное на 71×
служил и для обозначения отрицательного числа. Неизвестную величину он называл premier («первое число»), а ее степени – вторыми, третьими и т. д, числами. Записи степеней неизвестной у Шюке лаконичны. Например, современные символы 5, 5ж, 5х, 5х2, 5х3 у него выглядели бы так: 5°, 51, 52, 53. Вместо равенства 8х3×7х-1 = 56х2 Шюке писал: «83, умноженное на 71×  , дает 562». Таким образом, он рассматривал и отрицательные показатели. Относительно свободных членов уравнения Шюке указывал, что эти числа «имеют имя нуль».
, дает 562». Таким образом, он рассматривал и отрицательные показатели. Относительно свободных членов уравнения Шюке указывал, что эти числа «имеют имя нуль».
|
|
|
Значительного успеха в совершенствовании «алгебраических букв» Луки Пачоли достигли немецкие алгебраисты – «коссисты». Они вместо  и
и  ввели знаки + и –, знаки для неизвестной, и ее степеней, свободного члена.
ввели знаки + и –, знаки для неизвестной, и ее степеней, свободного члена.
XVI в. в алгебре ознаменовался величайшим открытием – решением в общем виде уравнений третьей и четвертой степеней.
Спицион дель Ферро в 1506 г. нашел решение кубического уравнения вида
x3 + ax = b a,b >0. (1)
Чуть позже Тарталья указал решение этого же уравнения в виде х =  -
-  , где u – v = b, uv =
, где u – v = b, uv =  , откуда u и v находятся как корни квадратного уравнения.
, откуда u и v находятся как корни квадратного уравнения.
Также он нашел решение уравнения x3 = ax + b a,b >0 (2)
в виде х =  +
+  , где u + v = b, uv =
, где u + v = b, uv =  .
.
Уравнение же x3 + b = ax a,b >0 можно решить с помощью уравнения (2).
В те времена предпочитали избегать отрицательных корней и задачи, сводящиеся к отрицательным корням уравнения (2), преобразовывали так, чтобы они приводили к положительным корням уравнения (3). Лишь Кардано позже осознал выгоду рассмотрения отрицательных корней.
Почему рассматривались только уравнения вида (1) и (2)? На этот вопрос ответ дал Кардано.
Чтобы разобраться в нем, рассмотрим полное уравнение третьей степени.
y3 + ay2 + by + c = 0.
Не следует думать, что Тарталья и Кардано писали такие уравнения. Нет, так стали поступать гораздо позже. Записывать все члены уравнения в одной части, приравнивая к одной части, начал Декарт. Да и символики не было, пользовались прообразами символов и словами. Уравнение x3 + ax = b записывалось примерно так: «куб» (х3)  некоторое количество (а) «вещей» (х) равно данному «числу» (b). Понять можно, но оперировать сложно.
некоторое количество (а) «вещей» (х) равно данному «числу» (b). Понять можно, но оперировать сложно.
Полное уравнение можно преобразовать в неполное, не содержащее члена с квадратом неизвестной. Сделаем замену y = x + a и подставим в уравнение; получим х3 + (3a + а)х2 + (3a2 + 2aа + b)x + (a3 + aa2 + ba + c) = 0.
Положим 3a + а = 0. Найдем отсюда a = - а/3 и подставим в выражения
p = 3a2 + 2aа + b, q = a3 + аa2 + ba + c.
Тогда уравнение примет вид х3 + px + q = 0.
В нашей символике это уравнение соответствует уравнениям (1), (2), которые решал Тарталья.
Кардано узнал способ решения уравнений третьей степени, предложенный Тартальи, опубликовал его. Формула же стала носить название «формулы Кардано».
|
|
|
Выведем теперь ее.
Рассмотрим уравнение х3 + px + q = 0. Введем новые неизвестные x = u + v и подставим их в исходное уравнение; получим u3 + v3 + (3uv + p)(u + v) + q = 0.
Приравняем 3uv + p к нулю: 3uv + p = 0.
Уравнение примет вид u3 + v3 + q = 0. Тогда uv = –  , u3v3 = –
, u3v3 = –  , u3 + v3 = -q.
, u3 + v3 = -q.
Выражения u3 и v3 можно принять за корни квадратного уравнения z2 + qz –  = 0.
= 0.
Решая его, получим z1 = –  +
+  , z2= –
, z2= –  –
–  .
.
Таким образом, x = u + v =  +
+  , x =
, x =  +
+  .
.
Это и есть формула Кардано. Не лишне заметить, что в таком виде Кардано ее не искал: он формулировал решение уравнений (1) и (2) и рассматривал связь между уравнениями (2) и (3).
В случае, когда  +
+  <0, под квадратным корнем получается отрицательное число и корень дает мнимость. Этот случай получил название неприводимого, так как решение уравнения третьей степени не приводится к решению квадратного уравнения. Как уже говорилось, с ним не справились ни Тарталья, ни Кардано. Его с помощью тригонометрии разобрал Виет.
<0, под квадратным корнем получается отрицательное число и корень дает мнимость. Этот случай получил название неприводимого, так как решение уравнения третьей степени не приводится к решению квадратного уравнения. Как уже говорилось, с ним не справились ни Тарталья, ни Кардано. Его с помощью тригонометрии разобрал Виет.
Чтобы получить представление о символике Кардано, приведем пример записи корня кубического уравнения x3 + 6x = 20. Выражение  записывалось так Rx.u.cu.Rx.108
записывалось так Rx.u.cu.Rx.108  10½
10½  Rx.u.cu.Rx.108
Rx.u.cu.Rx.108  10.
10.
Здесь Rx – знак корня (Radix), Rx.u.cu означает корень кубический из всего выражения до вертикальной черты или после нее,  и
и  - сокращения слов plus и minus.
- сокращения слов plus и minus.
Кардано показал, что легко можно решить уравнение x4  ax = bx2 +
ax = bx2 +  . Он привел его к виду x4 = b(x
. Он привел его к виду x4 = b(x 
 )2, а затем извлечением корня получил квадратное уравнение. Аналогично он рассматривал и некоторые другие виды уравнений.
)2, а затем извлечением корня получил квадратное уравнение. Аналогично он рассматривал и некоторые другие виды уравнений.
Однако уравнение x4 + 6x2 + 36 = 60x, предложенное да Кои Кардано не сумел решить.
Открыл метод решения уравнений четвертой степени 23 – летний ученик Кардано – Луиджи Феррари.
После того, как были исследованы уравнения третьей степени, задача об уравнениях четвертой степени стала более легкой. Феррари рассматривал уравнение, не содержащее члена с x3, т.е. уравнение вида x4 + ax2 + bx + c = 0.
Он преобразовывал его так, чтобы в левой части был полный квадрат, а в правой – выражение не выше второй степени относительно x.
|
|
|
Выделением полного квадрата получалось  = x4 + ax +
= x4 + ax +  = -bx – c +
= -bx – c +  ,
,  = -bx – c +
= -bx – c +  .
.
Теперь следовало выполнить такие преобразования, чтобы из левой и правой частей можно было извлечь корень. С этой целью Феррари вводил новую переменную t и прибавлял к обеим частям выражение 2  t + t2. Это дает
t + t2. Это дает  = 2tx2 – bx – c + at +
= 2tx2 – bx – c + at +  + t2,
+ t2,  = 2tx2 – bx + (– c +
= 2tx2 – bx + (– c +  + at + t2).
+ at + t2).
Нужно, чтобы правая часть была полным квадратом. Вспомним, как обстоит дело с трехчленом ax2 + bx + c. Выделим в нем полный квадрат: ax2 + bx + c = а(x2 +  x +
x +  ) = =a(x2 + 2x×
) = =a(x2 + 2x×  +
+  -
-  +
+  ) = a(x2 + 2x×
) = a(x2 + 2x× 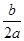 +
+  +
+  ) = a(x+
) = a(x+ 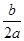 )2 +
)2 +  .
.
Трехчлен будет полным квадратом, когда 4ac – b2 = 0. В нашем случае роль коэффициента при x2 играет 2t, а роль свободного члена - выражение в скобках правой части уравнения. Тогда выражению 4ac – b2 = 0 соответствует 4×2t(t2 + at +  - c) – b2 = 0, b2 = 2t(4t2 + 4at + a2 - 4c).
- c) – b2 = 0, b2 = 2t(4t2 + 4at + a2 - 4c).
Таким образом, нахождение t свелось к решению кубического уравнения, а x находится з квадратного уравнения после извлечения корня из левой и правой частей, т.е. из уравнения x2 + 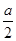 + t0 =
+ t0 =  .
.
Кардано отмечает, что таким же приемом можно решать уравнения, в которых отсутствует член не с третьей степенью х, а с первой. В этом случае делается подстановка х = k/y.
Открытия, сделанные итальянцами в алгебре и систематически изложенные Кардано, стали доступны математикам других стран и дали импульс развитию науки.
Дальнейшее развитие алгебры было связано с совершенствованием символики и разработкой общих методов решения уравнений.
В этом преуспел Франсуа Виета.
|
|
|


