 |
Высказывания и булевы функции
|
|
|
|
Одной из основных задач алгебры высказываний является установление значения истинности сложных высказываний в зависимости от значения истинности входящих в них простых высказываний. Для этого целесообразно рассматривать сложные высказывания как функции входящих в них простых высказываний. С другой стороны, так как значение истинности (и или л) сложного высказывания зависит по определению логических связок не от самих простых высказываний, а лишь от их значения истинности, то можно считать, что любое сложное высказывание определяет функцию, аргументы которой независимо друг от друга принимают значения и или л, а значение самой функции также принадлежит множеству {и, л} (конечно, существенно не то, что речь идет о функциях от нескольких аргументов из множества {и, л} в множество {и, л}, а лишь то, что данные множества двухэлементны. Эти множества зачастую обозначают не через {и, л}, а, например, через {0, 1}, считая, что 1 означает «истину», а 0 – «ложь»).
Такие функции называются булевыми функциями (по имени Д. Буля). Например, формула F (а, b, с) = (а Ù b) Þ (с Ù а) описывает, учитывая определение входящих в нее связок, булеву функцию, задаваемую следующей таблицей:
| а | b | с | F(a, b, с) | а | b | с | F(a, b, с) |
| и | и | и | и | л | и | и | и |
| и | и | л | л | л | и | л | и |
| и | л | и | и | л | л | и | и |
| и | л | л | и | л | л | л | и |
Заметим, что булевых функций от n аргументов имеется лишь конечное число, а именно столько, сколько возможно функциональных таблиц. Число возможных наборов аргументов равно 2n, а каждому набору аргументов можно независимо друг от друга сопоставлять одно из значений и или л. Таким образом, число всевозможных булевых функций от n аргументов равно  – Оно очень быстро растет с ростом n. Изучение свойств булевых функций имеет большее значение как для алгебры и математической логики, так и для их приложений в кибернетике и теории автоматов. Естественно распространить определение высказывательных связок, так как мы их определили выше, на булевы функции. Мы ограничимся рассмотрением лишь связок Ù, Ú, ù называемых булевыми связками (или булевыми операциями). Такое ограничение оправдано тем, что, как легко проверить, связки Þ и Û могут быть выражены через другие булевы связки. При помощи таблиц истинности, приведенных выше, легко проверяются следующие тождества:
– Оно очень быстро растет с ростом n. Изучение свойств булевых функций имеет большее значение как для алгебры и математической логики, так и для их приложений в кибернетике и теории автоматов. Естественно распространить определение высказывательных связок, так как мы их определили выше, на булевы функции. Мы ограничимся рассмотрением лишь связок Ù, Ú, ù называемых булевыми связками (или булевыми операциями). Такое ограничение оправдано тем, что, как легко проверить, связки Þ и Û могут быть выражены через другие булевы связки. При помощи таблиц истинности, приведенных выше, легко проверяются следующие тождества:
|
|
|
a Þ b º (ù a) Ú b;
a Û b º (a Ù b) Ú (ù a Ù ùb),
которые позволяют повсеместно заменить связки Þ, Û на Ù, Ú, ù.
Если мы теперь имеем булевы функции {F (xl, х2,..., хn), G (х1, х2,..., хn)} от n переменных, то действие связок над ними определяется естественным образом:
F (xl, x2,..., хn) Ù G (х1, x2,..., хn), F (xl, x2,...,хn) Ú G (xl, x2,..., хn), ùF (xl, x2,..., хn) – это такие булевы функции, которые принимают значения, предписываемые соответствующими таблицами для каждого возможного значения аргументов. Кратко: булевы операции так переносятся на булевы функции, как действия арифметики переносятся на обычные функции числовых аргументов. Вообще имеет место далеко идущая аналогия между обычной алгеброй чисел и числовыми функциями, с одной стороны, и высказываниями и булевыми функциями – с другой. При этом можно отметить, что в одном определенном смысле алгебра булевых функций проще алгебры числовых функций: если рассматривать лишь функции некоторого конечного числа аргументов, то таких функций лишь конечное число. Поэтому выкладки с булевыми функциями вполне доступны пониманию школьников старших классов.
Естественно, закономерности булевой алгебры менее привычны и вызывают удивление и недоверие: это судьба всякого новшества.
|
|
|
Выпишем законы булевой алгебры. Большими латинскими буквами А, В,..., X, Y, Z мы обозначим объекты, над которыми осуществляются булевы операции Ù, Ú, ù. Для определенности будем считать, что эти объекты – булевы функции некоторого фиксированного числа переменных. Среди них есть два особых элемента: 1, 0. Это соответственно функции, принимающие для всех аргументов значения 0 и 1 (постоянные функции – нуль и единица). Тогда
А Ù В = В Ù А, A Ú B = B Ú A
A Ù (В Ù C) = (А Ù В) Ù C A Ú (В Ú C) = (А Ú В) Ú C
A Ù A = A A Ú A = A
A Ù 1 = A A Ú 1 = A
A Ù 0 = 0 A Ú 0 = A
ù(A Ù B) = ùA Ú ùB ù(A Ú B) = ùA Ù ùB
A Ù (B Ú C) = (A Ù B) Ú (A Ù C) A Ú (B Ù C) = (A Ú B) Ù (A Ú C)
ù ùA = A
Если, как это обычно делают, булевы операции Ú, Ù, ù считать аналогом сложения, умножения и перехода к противоположному числу, то некоторые из вышеприведенных законов те же, что для числового сложения и умножения, другие же существенно отличаются от привычных.
Задания для учащихся.
Верно ли высказывание: ù(205 кратно 5); 7  7; ù(8>10); 1£3£3.
7; ù(8>10); 1£3£3.
А – множество точек треугольника и В – множество точек четырехугольника.

Верно ли высказывание: CÎA Ù CÎB; KÎB Ù KÎA; SÎB Ú SÎA; ù(SÎA)ÙSÎB?
Известно, что А=и, В=и, Х=л, Y=л. Найдите значение высказывания:
АÚùХ; ùYÙùA; AÞX; ù(ùВÚY); (AÙB)ÚX; (XÚB)ÞY; (XÙA)Þ(YÚB); ù (AÚX)Ù(YÚùX).
Составьте таблицу истинности высказываний: ùХÙХ; (ХÚY)ÚùY; (XÙY)ÚùX; ùXÞY; (XÙY)ÞY.
Используя переменные X, Y, Z, запишите сочетательное свойство операции «и».
Проверьте равенство (XÚY)ÙZ º (XÙZ)Ú(YÙZ) и (XÙY)ÚZº(XÚZ)Ù(YÚZ), составляя таблицы истинности для левой и правой части.
|
|
|
Предикаты и кванторы.
Предикаты.
Алгебра предикатов – тот раздел математической логики, который непосредственно надстраивается над алгеброй высказываний.
Как мы видели, одной из основных задач алгебры высказываний является изучение истинности или ложности высказываний в зависимости от истинности или ложности входящих в них высказываний. Несмотря на большую важность этой области логики, она оказывается слишком бедной для описания и для изучения даже простейших заключений науки и практики. В рамки алгебры высказываний не укладываются ни простейшие заключения арифметики и геометрии, не говоря уже о довольно сложных логических выводах, с которыми мы сталкиваемся в других науках и в повседневной жизни.
Действительно, рассмотрим следующие простейшие заключения.
Из истинных высказываний «3 меньше 5» и «5 меньше 7» мы заключаем, что «3 меньше 7». Из истинных высказываний «Все птицы – животные» и «Все воробьи – птицы» мы делаем заключение: «Все воробьи – животные». Из высказываний «Петр – сын Ивана» и «Павел – сын Петра» мы заключаем: «Павел – внук Ивана» и т. д.
Заметим, что во всех рассмотренных примерах истинность заключения зависит не только от истинности посылок, но и от их содержания. Если изменить вид посылок, то может оказаться, что заключение будет неверным. Так (в первом примере) из истинных высказываний «3 меньше 5» и «5 не равно 7» нельзя делать заключение (которое оказывается истинным), что «3 меньше 7», или, изменив немного второй пример, из истинных высказываний «Все птицы – животные» и «Никакие рыбы не птицы» нельзя выводить ни ложное высказывание «Никакие рыбы не животные», ни истинное высказывание «Все рыбы – животные». Наконец, видоизменив последний пример, из истинных высказываний «Петр – сын Ивана» и «Павел – родственник Петра» мы не имеем права делать заключение (которое в действительности может быть как истинным, так и ложным), что «Павел – внук Ивана» (но можем вывести истинное заключение: «Павел – родственник Ивана»).
Чтобы построить систему правил, позволяющую логически выводить правильные заключения, учитывающие в какой-то мере содержание посылок, мы должны проанализировать строение простых высказываний. И здесь нам опять кое-что может подсказать грамматика. Следуя по такому пути, мы придем к разделу логики, называемому алгеброй предикатов. Она предполагает алгебру высказываний уже известной, но идет дальше: простые высказывания, из которых состоят сложные, в свою очередь расчленяются.
|
|
|
Теория предикатов исходит из следующей установки. Простые высказывания выражают, что некоторые объекты обладают некоторыми свойствами или находятся между собой в некоторых отношениях.
При этом понятия «свойство» и «отношение» рассматриваются как частные случаи общего понятия «предиката». Объекты, о которых говорится в высказываниях, называются «термами». Постараемся выяснить смысл этих понятий на примерах.
Рассмотрим сначала некоторое число простых предложений – высказываний, выражающих, что некоторый объект обладает некоторым свойством:
«Сократ – грек»;
«Платон – ученик Сократа»;
«Три – простое число»;
«Василий – студент» и т. д.,
Все приведенные примеры – простые предложения, С точки зрения грамматики они состоят из подлежащего («Сократ», «Платон», «три», «Москва», «Василий») и сказуемого («есть грек», «есть ученик Сократа», «есть простое число»). Подлежащее является наименованием некоторого объекта – конкретного или абстрактного, сказуемое выражает некоторое свойство. В латинской грамматике сказуемое называется предикатом, и этим термином принято теперь пользоваться в математической логике в рассматриваемых ситуациях. Основным для алгебры предикатов является второй член предложения – сказуемое-свойство. Как же алгебра предикатов трактует понятие «свойство»? Она рассматривает его как некоторую функцию следующим образом.
Возьмем первый пример: «Сократ есть грек».
Вместо человека Сократ мы можем подставить имена всевозможных людей и будем получать всегда осмысленные предложения. Одни предложения будут истинными, другие – ложными:
«Сократ есть грек» – истинно;
«Платон есть грек» – истинно;
«Наполеон есть грек» – ложно;
«Ньютон есть грек» – ложно и т. д.
Более обще можно рассматривать выражение вида «X есть грек», где буква X указывает место, на которое нужно подставить имя некоторого человека, чтобы получить высказывание — истинное или ложное. Но, как нам уже известно, существенным свойством высказывания является его значение истинности и или л. Становясь на эту точку зрения, логика предикатов считает выражение «X есть грек» функцией, аргумент которой X пробегает класс всех людей, а сама функция принимает в качестве значений и или л. Если мы будем, как это принято в математике, «X есть грек» записывать сокращенно, например в виде Гр (X), то для значения X = Сократ получим Гр (Сократ) – и, а скажем Гр (Наполеон) – л и т. д. Относительно других приведенных примеров можно дословно повторить все то, что было сказано относительно первого.
|
|
|
Таким образом, предикатом или, лучше, предикатом-свойством будем считать функцию, определенную на некотором универсальном множестве и принимающую значения и и л. Те элементы, для которых значение предиката «истинно», обладают данным свойством, остальные не обладают.
Отсюда сразу видно, что в действительности всякий предикат-свойство вполне определяется подмножеством тех объектов, на которых данная функция принимает значение «истинно». Полезно привести примеры предикатов-свойств из области арифметики. Такими будут, например, свойства натуральных чисел «быть простым числом», «быть четным числом», «быть квадратом» и т. д.
Остановимся на примере «три есть простое число» и на соответствующем предикате-свойстве «быть простым числом». Введем для этого свойства сокращенное обозначение Пр (X). Предикат Пр (X) определен на множестве натуральных чисел. Имеем Пр(1) = л (поскольку 1 не принято рассматривать как простое число). Пр (2) = и, Пр (3) = и, Пр (4) = л,..., Пр (10) = л, Пр (11) = и и т. д.
Подобно приведенным предикатам-свойствам, математическая логика рассматривает более общее понятие предиката-отношения. В зависимости от того, между каким числом объектов устанавливается отношение, мы различаем двухместные (бинарные), трехместные (тернарные) и т. д., в общем случае – n-местные отношения. Рассмотренные выше предикаты-свойства считаются унарными предикатами. Наконец, оказывается удобным в понятие предиката-отношения как частный случай включить и высказывания в качестве «0 – местных предикатов».
Все математические дисциплины имеют дело с предикатами-отношениями, причем самыми распространенными являются бинарные отношения. Они описываются, различными словами: «равны», «не равны», «больше», «меньше», «делить», «перпендикулярны», «параллельны» и т. д.
По аналогии с предикатом-свойством двухместным предикатом считается опять функция, на этот раз от двух аргументов, определенных на некотором универсальном множестве, принимающая значение и (истинно) и л (ложно): те пары элементов, для которых функция принимает значение и, находятся в рассматриваемом отношении, остальные пары в этом отношении не находятся.
Рассмотрим пример бинарного отношения, определенного на множестве натуральных чисел, а именно отношение, описываемое словом «больше». Если рассматривать это отношение как функцию от двух переменных X и Y (на множестве натуральных чисел), принимающую значения и или л в зависимости от того, будет ли соответствующее отношение выполняться или нет, то эта функция определяет предикат, который обозначим через > (X, Y). Тогда имеем, например, > (3, 2) = и, > (1, 3) = л, > (7, 5) = и и т. д. Более полно и обозримо двухместный предикаты >(Х, Y).
| 1 | 2 | 3 | 4 | 5 | … | |
| 1 | л | и | и | и | и | … |
| 2 | л | л | и | и | и | … |
| 3 | л | л | л | и | и | … |
| 4 | л | л | л | л | и | … |
| 5 | л | л | л | л | л | … |
| … | … | … | … | … | … | … |
Конечно, совсем нетрудно указать в элементарной математике примеры трехместных предикатов и предикатов от еще большего числа аргументов. Так, трехместным предикатом является в геометрии отношение, описываемое словом «между»: «Точка Y лежит между точками X и Z». В арифметике хорошо известны понятия наибольшего общего делителя и наименьшего общего кратного двух целых чисел: фраза «Число d является наибольшим общим делителем чисел а и b» описывает трехместный предикат. Трехместные предикаты на множестве действительных чисел задают действия сложения, вычитания, умножения и деления: X + Y = Z, X – У = Z, X • Y = Z, X: Y = Z. Примером четырехместного предиката может служить отношение между членами пропорции X: Y = Z: W
Ознакомившись с понятием предиката, мы переходим теперь к рассмотрению операций, позволяющих из некоторых исходных предикатов строить новые. Начнем изучение с простейшего случая одноместных предикатов. Пусть Р (X) и Q (X) – два одноместных предиката, определенных на некотором множестве М. С помощью операций алгебры высказываний мы можем строить новые предикаты на множестве М. Конъюнкция Р (X)ÙQ (X) – это предикат R1(X) = Р(X)ÙQ(X), который истинен для тех объектов а из М, для которых оба предиката Р(X) и Q(X) истинны. Аналогично определяется дизъюнкция Р(X)ÚQ(X):R2(X) = Р(X)ÚQ(X) – это предикат на М, который истинен в точности для тех а  М, для которых истинен по меньшей мере один из предикатов Р (X) и Q (X). Так же определяется отрицание ùР (X): R3(X) = ùР(X) – предикат на М, истинный для тех и только тех а Î М, для которых Р (X) ложен.
М, для которых истинен по меньшей мере один из предикатов Р (X) и Q (X). Так же определяется отрицание ùР (X): R3(X) = ùР(X) – предикат на М, истинный для тех и только тех а Î М, для которых Р (X) ложен.
Кванторы.
В алгебре предикатов наряду с операциями логики высказываний важнейшую роль играют операции, называемые кванторами. Именно употребление кванторов делает алгебру предикатов значительно более богатой, чем алгебру высказываний. Кванторы соответствуют по смыслу тому, что на обычном языке выражается словами «все» («для каждого», «для всех» и т. п.) и «существует» («некоторый», «найдется» и т. п.).
Понятие, обозначаемое словом «все», лежит в основе квантора всеобщности (или квантора общности). Если через Гр (X) обозначен предикат «X есть грек», определенный на множестве М всех людей, то из этого предиката с помощью слова «все» мы можем построить высказывание «Все люди – греки» (конечно, ложное высказывание). Это пример применения квантора всеобщности.
Вообще же квантор всеобщности определяется так. Пусть Р (X) – какой-нибудь предикат. Тогда квантор всеобщности – это операция, которая сопоставляет Р (X) высказывание
«Все X обладают свойством Р (X)». (*)
Для этой операции («все») употребляется знак 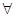 (перевернутая латинская буква А, напоминающая о немецком слове «alle» или английском «all» – все). Высказывание (*) записывается так:
(перевернутая латинская буква А, напоминающая о немецком слове «alle» или английском «all» – все). Высказывание (*) записывается так: 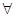 (X)P(X) (читается: «для всех X Р от X»). В соответствии со смыслом слова «все»
(X)P(X) (читается: «для всех X Р от X»). В соответствии со смыслом слова «все»  (X)Р(X) – ложное высказывание, кроме того единственного случая, когда Р (X) тождественно-истинный предикат.
(X)Р(X) – ложное высказывание, кроме того единственного случая, когда Р (X) тождественно-истинный предикат.
Наряду с квантором всеобщности в логике предикатов рассматривается другой квантор – «двойственный» ему квантор существования, обозначаемый знаком  (это перевернутая латинская буква E, напоминающая немецкое слово «existieren» или английское «exist» — существовать):
(это перевернутая латинская буква E, напоминающая немецкое слово «existieren» или английское «exist» — существовать):
 (Х)Р(Х)
(Х)Р(Х)
(читается: «существует такое X, что Р от X») – высказывание, которое истинно тогда и только тогда, когда Р истинно по меньшей мере для одного объекта а из области определения М. Тем самым 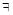 (X)Р(X) – истинное высказывание для всех предикатов Р (X), кроме одного – тождественно-ложного.
(X)Р(X) – истинное высказывание для всех предикатов Р (X), кроме одного – тождественно-ложного.
Между кванторами  и
и  имеют место отношения равносильности, позволяющие сводить любой из этих кванторов к другому: ù
имеют место отношения равносильности, позволяющие сводить любой из этих кванторов к другому: ù  (X) P(X) Û
(X) P(X) Û  (X) ù P(X) («Неверно, что все X обладают свойством Р (X)» равносильно тому, что «Существует такой объект X, для которого истинно не Р (X)»). Отсюда имеем:
(X) ù P(X) («Неверно, что все X обладают свойством Р (X)» равносильно тому, что «Существует такой объект X, для которого истинно не Р (X)»). Отсюда имеем:  (X) Û ù
(X) Û ù  (X)ù P(X). Аналогично, имеет место двойственный закон: ù
(X)ù P(X). Аналогично, имеет место двойственный закон: ù  (X) P(X) Û
(X) P(X) Û  (X)ù P(X). («Неверно, что существует X, обладающее свойством Р (X)» равносильно «Все X обладают свойством не Р (X)»).
(X)ù P(X). («Неверно, что существует X, обладающее свойством Р (X)» равносильно «Все X обладают свойством не Р (X)»).
Отсюда  (X)Р(X)Ûù
(X)Р(X)Ûù  (X)ùP(X). Эти равносильности называют правилами де Моргана для кванторов.
(X)ùP(X). Эти равносильности называют правилами де Моргана для кванторов.
С помощью квантора существования легко выражается суждение типа «Некоторые Р суть Q» (например, «Некоторые англичане курят», «Некоторые нечетные числа – простые» и т. п.), т. е. что по крайней мере один объект а, обладающий свойством Р, обладает также свойством Q. Этот факт записывается формулой  (X)(Р(X)ÙQ(X)) («Существует такой X, что Р от X и Q от X»).
(X)(Р(X)ÙQ(X)) («Существует такой X, что Р от X и Q от X»).
Аналогично с помощью кванторов записывается ряд других отношений между одноместными предикатами.
Гораздо более богатые возможности открывает применение кванторов к многоместным предикатам. Остановимся вкратце на этом вопросе.
Пусть А (X, Y) – некоторый двухместный предикат, определенный на некотором множестве М. Квантор всеобщности и квантор существования можно применять к нему как для переменной X, так и для переменной Y:  (X)А(X, У);
(X)А(X, У);  (Y)А(X, Y);
(Y)А(X, Y);  (X)А(Х,Y);
(X)А(Х,Y);  (Y)A(X,Y). Переменная, к которой применен квантор, называется связанной, другая переменная – свободной. Все четыре приведенных выражения являются записями одноместных предикатов от соответствующей свободной переменной.
(Y)A(X,Y). Переменная, к которой применен квантор, называется связанной, другая переменная – свободной. Все четыре приведенных выражения являются записями одноместных предикатов от соответствующей свободной переменной.  (X)А(X,Y) (читается: «для всех X, A от X и Y») – одноместный предикат от переменной Y:
(X)А(X,Y) (читается: «для всех X, A от X и Y») – одноместный предикат от переменной Y:  (X)А (X,Y)=F(У), Он истинен в точности для тех bÎМ, для которых одноместный предикат А (X, b) истинен для всех X. Если представить предикат А (X, Y) его таблицей, то предикат F (Y) =
(X)А (X,Y)=F(У), Он истинен в точности для тех bÎМ, для которых одноместный предикат А (X, b) истинен для всех X. Если представить предикат А (X, Y) его таблицей, то предикат F (Y) =  (X) (X, Y) истинен для тех b, для которых столбец с входом b содержит исключительно букву и.
(X) (X, Y) истинен для тех b, для которых столбец с входом b содержит исключительно букву и.
Применение квантора к одной из переменных двухместного предиката превращает его в одноместный. В случае трехместных предикатов применение квантора приводит к двухместному предикату. Аналогично и для предикатов с большим числом мест применение квантора превращает n-местный предикат в (n – 1)-местный.
К свободной переменной X одноместного предиката  (У)А(X, Y) в свою очередь можно применять квантор всеобщности или квантор существования. Получаются выражения
(У)А(X, Y) в свою очередь можно применять квантор всеобщности или квантор существования. Получаются выражения
 (X)(
(X)( (У)А(X,У));
(У)А(X,У));  (X)(
(X)( (Y)А(X,У)), которые, опуская скобки, принято записывать несколько проще:
(Y)А(X,У)), которые, опуская скобки, принято записывать несколько проще:  (X)
(X)  (У)А(X,У);
(У)А(X,У);  (X)
(X)  (Y)А(X,У),
(Y)А(X,У),
Это – высказывания. Первое истинно, если все строки, а тем самым и вся таблица предикатов, содержат только букву и, второе истинно, если соответствующая матрица содержит по меньшей мере одну тождественно-истинную строку. Три другие предиката  (X)А (X,У),
(X)А (X,У),  (У)А(X, У) и
(У)А(X, У) и  (X)А (X,У) также допускают квантификацию, так что в общей сложности мы получаем из одного предиката восемь формально различных высказываний:
(X)А (X,У) также допускают квантификацию, так что в общей сложности мы получаем из одного предиката восемь формально различных высказываний:  (X)
(X)  (У)А (X, У);
(У)А (X, У);  (X)
(X)  (У)А (X,У);
(У)А (X,У);  (X)
(X)  (У)А (X, У);
(У)А (X, У);  (X)
(X)  (У)А (X, У);
(У)А (X, У);  (У)
(У)  (X) А (X, У);
(X) А (X, У);  (У)
(У)  (X)А(X, У);
(X)А(X, У);  (У)
(У)  (X)А (X, У);
(X)А (X, У);  (Y)
(Y)  (X) А (X, У).
(X) А (X, У).
Нетрудно убедиться в том, что четыре высказывания, содержащие одинаковые кванторы, попарно эквивалентны:
 (X)
(X)  (У)А(X,У) Û
(У)А(X,У) Û  (У)
(У)  (X)А (X, У);
(X)А (X, У);
 (X)
(X)  (У)А (X, У) Û
(У)А (X, У) Û  (Y)
(Y)  (X)А (X, У).
(X)А (X, У).
 (X)
(X)  (У)А(X,У) так же как и
(У)А(X,У) так же как и  (У)
(У)  (X)А(X, У), истинно тогда и только тогда, когда А (X, У) – тождественно-истинный предикат,
(X)А(X, У), истинно тогда и только тогда, когда А (X, У) – тождественно-истинный предикат,  (X)
(X)  (У)А (X, У) и
(У)А (X, У) и  (Y)
(Y)  (X)А(X,У) оба истинны во всех случаях, кроме одного, когда А(X,У) – тождественно-ложный предикат. Все остальные высказывания существенно различны. Особенно следует помнить, что порядок следования разноименных кванторов очень важен.
(X)А(X,У) оба истинны во всех случаях, кроме одного, когда А(X,У) – тождественно-ложный предикат. Все остальные высказывания существенно различны. Особенно следует помнить, что порядок следования разноименных кванторов очень важен.
Я считаю, что к окончанию школы ученики должны овладеть кванторами, но введение их должно быть постепенным и начинаться в простых ситуациях. Учащиеся должны хорошо понимать, что от перестановки кванторов может меняться смысл утверждения.
Например, Пусть I=(а,b) – некоторый интервал. Тогда «Для всякого хÎI существует такой у, что у = f (х)» ( (x)
(x)  (у) (у = f (х))), означает, что функция f(х) всюду определена на I. Напротив, «Существует такое у, что для всякого х у=f (х)» (
(у) (у = f (х))), означает, что функция f(х) всюду определена на I. Напротив, «Существует такое у, что для всякого х у=f (х)» ( (у)
(у)  (х)(у=f(х))) означает, что функция f(x) принимает для всех х некоторое фиксированное значение у, т. е. постоянна.
(х)(у=f(х))) означает, что функция f(x) принимает для всех х некоторое фиксированное значение у, т. е. постоянна.
Приведем еще один пример. Корректное определение периодичности всюду определенной функции f(х) выглядит с использованием кванторов так:  (c)
(c)  (x) (c¹0 Ù Ùf(x+c) = f(x)), между тем если переставить кванторы и сформулировать утверждение «Для каждого х существует такое с, что с¹0 и что f(х + с) =f(x)»:
(x) (c¹0 Ù Ùf(x+c) = f(x)), между тем если переставить кванторы и сформулировать утверждение «Для каждого х существует такое с, что с¹0 и что f(х + с) =f(x)»:  (c)
(c)  (x) (c¹0 Ù f(x+c) = f(x)), то это означает лишь, что функция принимает каждое значение больше чем один раз, т. е. нечто совсем иное.
(x) (c¹0 Ù f(x+c) = f(x)), то это означает лишь, что функция принимает каждое значение больше чем один раз, т. е. нечто совсем иное.
В математическом анализе часто приходится сталкиваться с кванторами.
Определение предела последовательности из учебника «Алгебра и начала анализа» для 10-11 классов сформулировано так «Число А является пределом последовательности аn, если для любого  >0 существует номер N, такой, что при всех n>N верно неравенство
>0 существует номер N, такой, что при всех n>N верно неравенство  ». В кванторном обозначении это определение записывается так:
». В кванторном обозначении это определение записывается так:
 (
(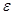 >0)
>0)  (NÎN)
(NÎN)  (n ÎN)((n>N) Þ
(n ÎN)((n>N) Þ 
Переставлять кванторы нельзя: именно тот факт, что N под квантором существования  следует за выражением
следует за выражением  (
( > 0), указывает на зависимость N от выбранного
> 0), указывает на зависимость N от выбранного 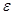 .
.
Как выразить утверждение, что последовательность (хn) сходится? Надо указать на то, что предел A существует. С помощью кванторов это утверждение формулируется так:
 (A)
(A)  (
( > 0)
> 0)  (NÎ N)
(NÎ N)  (nÎN)((n > N) Þ (
(nÎN)((n > N) Þ ( )).
)).
Такая запись имеет еще и то преимущество, что она почти автоматически позволяет формулировать отрицание существования предела, означающее свойство расходимости. Для этого достаточно несколько раз применить правило де Моргана для кванторов: (хn) расходится Ûù( (A)
(A)  (
( > 0)
> 0)  (NÎ N)
(NÎ N)  (nÎN)((n > N) Þ (
(nÎN)((n > N) Þ ( )) Û
)) Û  (A)
(A)  (
(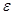 > 0)
> 0)  (NÎ N)
(NÎ N)  (nÎN)((n > N) Ù
(nÎN)((n > N) Ù  ).
).
Задания для учащихся.
Установите, какие из следующих высказываний истинны.
 x (x + 1 = x);
x (x + 1 = x);  x (x2 + x + 1>0);
x (x2 + x + 1>0);  x (x2 - 5x + 6>0);
x (x2 - 5x + 6>0);  x (x2 -6x+8³0 Ù x2-4x+3>0);
x (x2 -6x+8³0 Ù x2-4x+3>0);  x (x2 - 5x + 6 ³ 0 Ú x2 + 5x + 6 < 0)
x (x2 - 5x + 6 ³ 0 Ú x2 + 5x + 6 < 0)
2) При каких аÎR истинны следующие высказывания:  х (x2 +x + а>0);
х (x2 +x + а>0);
 x (x2 +x + а>0);
x (x2 +x + а>0);  х (x2 +ax + 1>0);
х (x2 +ax + 1>0);
3) Пусть P(x) = «х – простое число»
E(x) = «х – четное число»
Z(x) = «х – целое число»
D(x,y) = «y делится на х»
G(x,y) = «х > y»
Расшифруйте следующие высказывания и выясните, какие из них истинны:
P(x)ÞùE(x);  x (E(x) Ú D(x,6));
x (E(x) Ú D(x,6));
 x(P(x)ÞùE(x);
x(P(x)ÞùE(x);  x(P(x)ÚE(x));
x(P(x)ÚE(x));
 x
x  y(D(x,y)ÞG(y,x));
y(D(x,y)ÞG(y,x));  x
x  y(Z(x)ÙZ(y)ÞD(x,y));
y(Z(x)ÙZ(y)ÞD(x,y));
 x
x  y(Z(x)ÙZ(y)ÞD(x,y)).
y(Z(x)ÙZ(y)ÞD(x,y)).
4) Запишите с помощью кванторов определение предела функции: число b называется пределом функции f(х) при х, стремящемся к а, если для любого положительного числа  найдется такое положительное число
найдется такое положительное число  , что при всех х ¹ а, удовлетворяющих неравенству ½х – а½<0, будет выполнено неравенство ½f (х) – b½<
, что при всех х ¹ а, удовлетворяющих неравенству ½х – а½<0, будет выполнено неравенство ½f (х) – b½< 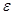 .
.
|
|
|


