 |
Параметры состояния. «Волновая функция»
|
|
|
|
Ещё одно отличие квантовой механики от классической физики, которое помогает понять природу принципа неопределённости, состоит в понятии мгновенного состояния физической системы.
В классической механике состояние системы из произвольного числа частиц в момент времени 
полностью описывается заданием для каждой частицы значений трёх координат частицы 
и трёх компонент импульса 
. Эти величины обычно называют «параметрами состояния» (переменными состояния).
Далее, если система остаётся изолированной в течение промежутка времени от до 
, то на основе заданного состояния системы при законы классической механики однозначно определяют её состояние (значение всех параметров состояния) при .
В квантовой механике множество параметров состояния для данной системы в данное время называется «полным», если, во-первых, в принципе возможно одновременно измерить все эти параметры и, во-вторых, для любого другого состояния значение параметра, который может быть измерен вместе с другими параметрами множества, будет определяться их значениями. Полное множество может состоять из следующих величин: для некоторых частиц - координаты 
, для других - компоненты импульса 
, для каких-либо других - наборы вида 
, 
, т.е. в любых терминах 
и 
. Согласно принципам квантовой механики, состояние системы в данный момент времени полностью описывается характеристикой значений любого полного множества параметров состояния. Очевидно, что такое описание будет рассматриваться как неполное с классической точки зрения, но такое ограничение описания находится в согласии с принципом неопределённости: если 
известно, то 
в принципе непознаваемо.
|
|
|
В квантовой механике любое состояние системы может быть представлено функцией специального вида - «волновой функцией» (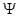
-функцией). Волновой функции соответствуют численные значения во всех точках пространства. Если значения полного множества параметров состояния для времени 
заданы, то волновая функция системы для будет определена однозначно. Такие волновые функции играют в квантовой механике роль, аналогичную функциям состояния в классической механике. При условиях можно определить волновую функцию для 
на основе данной волновой функции для . Это делается с помощью «дифференциального уравнения Шрёдингера», сформулированного известным австрийским физиком Эдвином Шрёдингером. Это уравнение имеет форму детерминистического закона.
Таким образом, если принять волновую функцию как полное представление мгновенного состояния, то необходимо признать, что, по крайней мере, на теоретическом уровне детерминизм сохраняется и в квантовой механике. Необходимо помнить, тем не менее, что знание значения волновой функции при не означает возможность абсолютно точного определения значения какого-либо параметра состояния частицы в этот момент времени. Волновая функция даёт только вероятностное распределение для всех возможных значений этой величины. И только в некоторых особых случаях эти значения теоретически достигают вероятности 1, позволяя сказать, что это значение точно предсказано. Квантовая теория фундаментально индетерминистична в том смысле, что она не обеспечивает точных предсказаний для будущих результатов измерений, а делает только вероятностные предсказания.
Случай макромира
Поскольку волновая функция, вычисленная для любого момента времени даёт относительно отдельных частиц вероятностное распределение параметров прежнего состояния, то можно вывести вероятностное распределение для других величин, которые определяются в терминах предшествующих. Многие из этих величин относятся к макронаблюдаемым свойствам таким, как температура, положение, скорости центра масс тела. Если тело состоит из миллиардов частиц, то его положение, скорость, температура и другие измеряемые величины можно будет вычислить с огромной точностью через вероятностные распределения каждой из частиц, составляющей тело. В этом случае кривая плотности вероятности для статистической величины имеет форму очень узкой, крутой возвышенности. Как следствие из этого, вероятность того, что значение данного параметра лежит в этом интервале, экстремально сходится к 1. При таком схождении для всех практических целей можно не рассматривать вероятностный характер предсказания и считать его достоверным. Но с точки зрения квантовой теории любое тело представляет систему, образованную из миллиардов частиц, и для каждой отдельной частицы существует неизбежная ошибка в предсказании. Неопределённость, выражаемая с помощью квантовых законов и в этом случае имеет место, но она сводится почти к нулю благодаря статистическим законам, охватывающим очень большое число частиц. С другой стороны, имеются ситуации совершенно другого характера, в которых появление события непосредственно наблюдаемо, но зависит от поведения крайне малого числа частиц, а иногда даже отдельной частицы. В случаях такого рода значительная неопределённость поведения частицы имеет место и в отношении к макрособытию. Это часто встречается в тех ситуациях, где радиоактивное микрособытие вызывает макрособытие, например, когда электроны, испускаемые при бета-распаде, производят отчётливо слышный щелчок в счётчик Гейгера. Даже если сделать идеальное предположение, что значения полного множества параметров первоначального состояния для субатомных частиц в небольшой совокупности радиоактивных атомов тела в момент времени известны, можно вычислить только вероятности появления таких событий, как, например: не испускается ни одна частица, испускается ода частица, две частицы и т.д. в течение первой секунды после .
|
|
|
Заключение
Таким образом, можно отметить, что проблема причинности и принципа детерминизма окончательно не решена.
|
|
|
Некоторые физики считают, что квантовая механика является незавершённым разделом физики, и впоследствии развитии теории отбросит принцип неопределённости Гейзенберга. Другие предсказывают наличие пока не изученных частиц на субмикроуровне, открытие которых объяснит вероятностное распределение параметров состояния. Большинство склоняется к той точке зрения, что принцип неопределённости характеризует процессы лишь на микроуровне; на макроуровне (за исключением некоторых макропроцессов, существенно зависящих от микропроцессов) можно считать достаточным асимптотическое стремление плотности вероятности к 1 в некоторой точке.
В конце XX и в начале XXI века приобретает силу новое направление в естественных и социальных науках - синергетика. В синергетике исследуются открытые самоорганизующиеся и саморазвивающиеся системы, описываемые нелинейными дифференциальными уравнениями.
Исследования в данном направлении в области физики (неравновесная термодинамика) показали в частности, что вероятность является не столько следствием незнания всех законов мира, в котором мы живём, сколько внутренней характеристикой динамической системы.
Список использованной литературы
1. Бунге М. Философия физики. - М, 2005.
2. Карнап Р. Философские основания физики. / Пер. с англ., под ред. Новика И.Б. - М.: «Прогресс». - 390 - с. 2000.
. Кедров Б.М. Научная концепция детерминизма. - М., 1993.
. Томпсон М. Философия науки. - М, 2003.
|
|
|
