 |
Подставив в (28 ), получим для индуцированного магнитного момента
|
|
|
|
Лекция 15
МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
Магнитный момент атома
Все вещества состоят из молекул и атомов.
Атом состоит из ядра, содержащего положительно заряженные протоны и нейтроны, не имеющие заряда. Вокруг ядра обращаются отрицательно заряженные электроны. При движении электрона вокруг ядра по орбите радиуса r со скоростью v возникает микроток
I = qen = 
, (1)
где n - частота обращения электрона по орбите; qe - заряд электрона.
Движение электрона по орбите характеризуют:
1) орбитальным магнитным моментом 
(рис.1), модуль которого
рm = IS = 
, где S = pr2 - площадь орбиты; (2)
Рис. 1
|
2) орбитальным моментом импульса 
, модуль которого Le = mvr, (3)
где m - масса электрона.
Вектор противоположен по направлению вектору .
Отношение 
(4)
называют гиромагнитным отношением.
Кроме орбитального, электрон обладает собственным (спиновым) моментом импульса - 
, с которым связан собственный магнитный момент 
, и характеризуется спиновым гиромагнитным отношением 
. (5)
Элементарным магнитным моментом электрона является магнетон Бора
. (6)
Чтобы найти полный магнитный момент атома, надо сложить магнитные моменты всех электронов, входящих в состав атома и магнитный момент ядра. Магнитный момент ядра в ≈1840 раз меньше магнитного момента электрона и в дальнейшем его рассматривать не будем.
Атом в магнитном поле
При движении электрона вокруг ядра по орбите радиуса r на него действует центростремительная сила
.
Если атом внести во внешнее магнитное поле, вектор индукции 
которого перпендикулярен плоскости орбиты электрона, то на электрон начнет действовать сила Лоренца
,
где w - круговая частота обращения электрона в магнитном поле.
|
|
|
Уравнение движения электрона в магнитном поле запишем в виде
mw2r = Fцс ± Fл
или
mw2r = 
± 
,
где знаки «±» выбираются в соответствии с относительной ориентацией векторов 
и 
.
После преобразования последнего выражения получим
mr(w - wo) (w + wo) = 2mrDw×w = ± qewrB,
где Dw =½w-wo ½<< w; 2w @ w+wo.
Из последнего выражения найдем, что
wL = Dw = ± 
или в векторном виде
. (7)
Таким образом, в магнитном поле электрон получает дополнительную угловую скорость вращения, которую называют частотой Лармора.
Причем векторы L и cовпадают по направлению (рис.4.12).
Рис. 2
|
Частоту Лармора приобретают все электроны атома, так как она не зависит от радиуса орбиты и скорости движения электрона.
Скорость электрона при внесении атома в магнитное поле изменяется, поэтому изменяется и его кинетическая энергия Wk.
Но так как радиус вращения остается неизменным, то потенциальная энергия электрона не изменяется.
За счет чего же изменяется энергия электрона в атоме, если магнитное поле действует перпендикулярно скорости и не производит работы?
Частота Лармора возникает в момент включения магнитного поля.
Следовательно, переменное магнитное поле возбуждает переменное электрическое поле, которое и сообщает электрону дополнительное вращение с частотой Лармора.
Таким образом, возникновение ларморовского вращения вызвано проявлением электромагнитной индукции.
Это явление наблюдается во всех без исключения веществах при внесении их в магнитное поле. Векторы и начинают прецессировать вокруг направления с частотой Лармора (вектор описывает коническую поверхность, рис. 2.).
Теорема Лармора: Единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора с угловой скоростью L вокруг оси, проходящей через ядро атома и параллельно вектору индукции внешнего магнитного поля.
|
|
|
Рис. 3
|
В результате прецессии наводится дополнительный орбитальный магнитный момент электрона, модуль которого
Dрm = DI×S^ = 
, (8)
где DI = qeDn, wL = 2pDn; S^ - площадь проекции орбиты электрона на плоскость, перпендикулярную (рис. 3).
Так как вектор D противоположен по направлению вектору , то
D = 
. (9)
Если атом содержит Z электронов, то наведенный магнитный момент
D = 
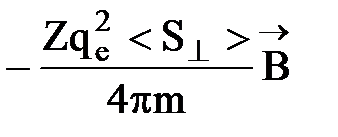, (10)
где < S^ > - cреднее значение площади S^ для орбит всех электронов атома.
При суммировании орбитальных и спиновых магнитных моментов атомов может произойти их полная компенсация.
Тогда результирующий магнитный момент атома равен нулю.
Если такой компенсации не происходит, то атом имеет постоянный магнитный момент. Вещества, у которых атомы в отсутствие внешнего магнитного поля имеют постоянный магнитный момент, не равный нулю, могут быть парамагнетиками, ферромагнетиками, антиферромагнетиками или ферримагнетиками.
Вектор намагничивания
Любое вещество при внесении его во внешнее магнитное поле намагничивается в той или иной степени. Количественной характеристикой вещества в магнитном поле является вектор намагничивания 
.
Суммарный магнитный момент единицы объема вещества называют вектором намагничивания.
, (11)
где 
- магнитный момент i-го атома (молекулы) из их общего числа, в объeме DV. В СИ намагниченность измеряется в А/м.
Магнитное поле в веществе
Любое вещество при внесении его во внешнее магнитное поле 
приобретает магнитный момент, т.е. намагничивается. Намагниченное вещество создает собственное магнитное поле 
. Согласно принципу суперпозиции результирующее магнитное поле
= + . (12)
Следовательно, намагничивание вещества обусловлено преимущественной ориентацией магнитных моментов молекул в одном направлении.
Это положение распространяется и на элементарные молекулярные токи (гипотеза Ампера).
Такое поведение молекулярных токов приводит к появлению макроскопических токов I*, называемых токами намагничивания.
Молекулярные токи в однородном магнетике ориентированы, как показано на рис. 4, а. У соседних молекул молекулярные токи в местах их соприкосновения
Рис. 4
|
текут в противоположных направлениях и взаимно компенсируют друг друга.
|
|
|
Молекулярные токи, которые выходят на боковую поверхность цилиндрического образца оказываются некомпенсированными и создают поверхностный ток намагничивания I*.
Внутри неоднородного намагниченного магнетика компенсации молекулярных токов нет, так как сила тока в направлении оси Х возрастает, и возникает объемный ток намагничивания. Вектор 
направлен за плоскость рисунка (обозначен символом Å) и увеличивается по модулю при возрастании координаты Х (рис. 4, б). Однако распределение токов намагничивания зависит не только от формы и свойств магнетика, но и от искомого поля . В общем случае задача о нахождении поля в магнетике непосредственно решена быть не может.
Для решения этого вопроса необходимо установить связь между током намагничивания I* и циркуляцией поля вектора намагничивания .
5. Циркуляция вектора
Теорема: В стационарном состоянии циркуляция намагниченности по произвольному замкнутому контуру L равна алгебраической сумме токов намагничивания I*, охватываемых этим контуром, т. е.
. (13)
Натянем на контур L произвольную поверхность S (рис. 5).
Из рисунка видно, что одни молекулярные токи пересекают поверхность S дважды в разных направлениях, поэтому не вносят вклада в результирующий ток намагничивания через эту поверхность.
Другие молекулярные токи пересекают поверхность S только один раз, поэтому и создают макроскопический ток намагничивания, пронизывающий эту поверхность.
Рис. 5
|
Пусть элементарная площадь Sмол охватывает каждый молекулярный ток Iмол.
Элемент d 
контура L (рис. 6) обвивают те молекулярные токи, центры которых попадают внутрь цилиндра с объемом dV= Sмолсosa d , где a - угол между направлением вектора и элементом 
.
Рис. 6
|
Эти молекулярные токи пересекают поверхность S только один раз и вносят вклад в ток намагничивания
dI* = IмолndV
или
dI* = IмолnSмолсosad = Jсosa = 
,
где n0 - концентрация молекул;
рm = IмолSмол -
магнитный момент отдельного молекулярного тока; nIмолSмол - магнитный момент единицы объема вещества.
|
|
|
После интегрирования по всему контуру L последнего выражения, получим формулу (13).
Поле вектора зависит от всех токов, как от тока намагничивания I*, так и от тока проводимости I.
6. Циркуляция вектора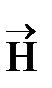 
При внесении вещества в магнитное поле возникают токи намагничивания, поэтому циркуляция вектора будет определяться не только токами проводимости I, но и токами намагничивания I*, т. е.
. (14)
Если циркуляция векторов и берется по одному и тому же контуру L, то, решив совместно (13) и (14), получим
(15)
где
(16)
- напряженность магнитного поля.
Следовательно,
. (17)
Эта формула выражает теорему о циркуляции вектора 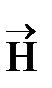: циркуляция вектора 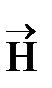по произвольному контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром.
Дифференциальная форма теоремы о циркуляции вектора 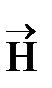записывается в виде
[ 
´ 
] = 
, (18)
т. е. ротор вектора 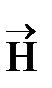равен плотности тока проводимости в той же точке вещества. Используя формулы (16), (17) и (18), имеем
(1+c) =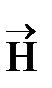 
.
Так как = mm0 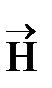, то m = 1 + c. (19)
7. Граничные условия для векторов 
и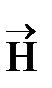
Найдем условия для векторов и 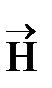на границе раздела двух однородных магнетиков.
Для нахождения условия для вектора применим теорему Гаусса, т. е.
. (20)
В качестве замкнутой поверхности возьмем малой высоты цилиндр, расположенный на границе раздела двух магнетиков (рис. 7).
Рис. 7.
|
Полный поток вектора сквозь цилиндрическую поверхность запишем с учетом того, что потоком сквозь боковую поверхность цилиндра можно пренебречь:
. (21)
При нахождении обеих проекций вектора на общую нормаль получим 
и после подстановки в предыдущее равенство получим
. (22)
Следовательно, нормальная составляющая вектора одинакова по обе стороны границы раздела магнетиков и скачка не испытывает.
При нахождении условия для вектора 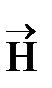используем теорему о циркуляции 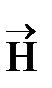, формула (17).
Предположим, что вдоль поверхности раздела двух магнетиков течет поверхностный ток проводимости с линейной плотностью i.
В качестве замкнутого контура L используем прямоугольник, высота которого мала по сравнению с его длиной (рис. 8).
Рис. 8
|
Циркуляция вектора 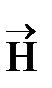на боковых сторонах контура L практически равна нулю. Поэтому циркуляцию вектора 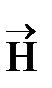запишем в виде
,
где iN - проекция вектора 
на нормаль 
к контуру (вектор образует с направлением обхода по контуру правовинтовую систему).
Обе проекции вектора 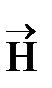возьмем на общий орт касательной 
(в магнетике 2), т. е.
.
С учетом этого предыдущее уравнение принимает вид
. (23)
Вывод: при переходе границы раздела двух магнетиков тангенциальная составляющая вектора 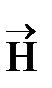испытывает скачок из-за наличия поверхностных токов проводимости.
|
|
|
Если же на границе раздела токов проводимости нет, то тангенциальная составляющая вектора 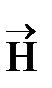не испытывает скачка, т. е.
. (24)
Таким образом, если на границе раздела двух однородных магнетиков тока проводимости нет, то составляющие Вt и Нn испытывают скачок. Составляющие Вn и Нt изменяются н с учетом этого в предыдущем уравнении (24) составляющие Н2t и Н1t не испытывают скачка, т. е. изменяются непрерывно.
8. Преломление линий вектора и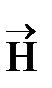
На границе раздела двух магнетиков с магнитными проницаемостями m1 и m2 (m1 < m2) линии вектора испытывают скачок, т. е. преломляются (рис. 9, а, б).
Рис. 9
|
Найдем отношение тангенсов углов a1 и a2:
. (25)
Если на границе раздела двух магнетиков тока проводимости нет, то
(26)
Поэтому закон преломления линий и линий 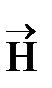запишем в виде
. (27)
На явлении преломления силовых линий магнитного поля основана защита приборов от влияния внешних магнитных полей, если их окружить экраном из ферромагнитного вещества, например, железа.
Природа диамагнетизма
Вещества, у которых в отсутствие внешнего магнитного поля результирующий магнитный момент равен нулю, называют диамагнетиками.
К ним относятся, например: инертные газы, молекулярный водород, азот, цинк, медь, золото и др. Диамагнитный эффект можно объяснить на примере инертных газов. Рассмотрим модель изотопа атома гелия 
. Атом гелия имеет в ядре 2 протона (положительный заряд qп = +2е и два нейтрона (qн = 0).
Рис. 10
|
Вокруг ядра обращаются два электрона (qе = -2е).
На электроны со стороны ядра действуют кулоновские силы. Если предположить, что оба электрона вращаются вокруг ядра с одинаковой скоростью, но в противоположном направлении и на одном и том же расстоянии от ядра (рис. 10), то их орбитальные магнитные моменты будут равны по величине, но противоположны по направлению, в отсутствие внешнего магнитного поля. Следовательно, суммарный магнитный момент атома гелия равен нулю. При внесении атома гелия в магнитное поле, на каждый из электронов будут действовать кулоновская сила и сила Лоренца (рис. 11). Их равнодействующая сообщит каждому электрону центростремительное ускорение. Уравнения движения электронов в магнитном поле можно записать в виде
| Рис. 11 |
, 
.
Из уравнений следует, что под действием магнитного поля скорость движения первого электрона уменьшилась, а второго - возросла. В связи с этим магнитный момент первого электрона уменьшится, а второго - увеличится. В результате этого у атома гелия индуцируется (наводится) дополнительный магнитный момент
(28)
Причем индуцированный магнитный момент DРм направлен противоположно вектору индукции внешнего магнитного поля.
Решая совместно уравнения движения электронов, имеем
или 
.
Подставив в (28), получим для индуцированного магнитного момента
. В векторном виде 
или 
.
При внесении диамагнетика во внешнее магнитное поле атомы (молекулы), входящие в его состав, согласно теореме Лармора приобретают индуцированный магнитный момент D . В пределах малого объема DV изотропного диамагнетика векторы D всех n атомов одинаковы, пропорциональны и противоположны ему по направлению.
Следовательно, вектор намагничивания диамагнетика
, (29)
где n0 - концентрация атомов; m0 - магнитная постоянная; c - диамагнитная восприимчивость.
Таблица 1
|
|
|
|
