 |
Внутренняя энергия магнетиков
|
|
|
|
dU = TdS + 
. (35)
Свободная энергия магнетика
dF = – SdT + . (36)
Термодинамический потенциал
dФ = – SdT – 
. (37)
Энтальпия магнетика
dI = TdS – . (38)
Уравнение состояния магнетика запишем в виде
В =f(Н, Т, r),
где Н – напряженность внешнего магнитного поля; Т – абсолютная температура; r – плотность магнетика.
Используя уравнение состояния (36) для свободной энергии, получаем следующее выражение:
F = ò + F0(Т, r), (39)
где F0 – значение свободной энергии при отсутствии магнитного поля.
После интегрирования (39) с учетом того, что В = mm0Н (при Т = const; r = const), имеет
. (40)
После интегрирования (35) найдем внутреннюю энергию магнетика:
, (41)
где U0 – внутренняя энергия магнетика в отсутствие магнитного поля.
Адиабатическое и квазистатическое изменение намагниченности 
приводит к изменению температуры (магнитокалорический эффект).
Из условия постоянства энтропии можно найти изменение температуры, если S = f(T, B); r = const, т. е.
, (42)
где СВ – теплоемкость единицы объема магнетика при В = const,
или 
, (43)
где СН – теплоемкость единицы объема магнетика при Н = const.
Применяя формулу (43) к парамагнетикам с учетом закона Кюри, согласно которому магнитная восприимчивость c парамагнитного образца пропорциональна абсолютной температуре, т. е.
, (44)
Получаем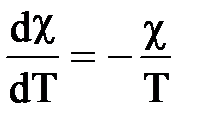 
. (45)
С учетом этого формула (43) принимает вид
. (46)
Следовательно, при обратимом адиабатическом размагничивании парамагнетик охлаждается.
Магнитное охлаждение
Атомы парамагнитных веществ обладают постоянным магнитным моментом. При отсутствии внешнего магнитного поля в результате теплового движения эти моменты ориентированы хаотично. Количественной мерой такого состояния является энтропия, которая в данном случае называется магнитной энтропией SМ. Согласно принципу Больцмана
|
|
|
SМ = k 
, (47)
где Wм – термодинамическая вероятность, равная числу способов распределения n атомов парамагнетика по подуровням, на которые расщепляется каждый уровень атома в магнитном поле. При наложении и увеличении магнитного поля вплоть до насыщения все магнитные моменты атомов ориентированы вдоль поля. Магнитная энтропия парамагнетика в этом состоянии обращается в нуль. Если процесс намагничивания парамагнитного образца происходит при постоянной температуре, то уменьшение энтропии на DS вызывает выделение теплоты DQ =T DS. Эта теплота отводится от образца в окружающую среду. В качестве такой среды используют жидкий гелий.
После установления равновесия гелий удаляется и образец оказывается теплоизолированным и подвергается медленному адиабатическому размагничиванию, при котором его магнитная энтропия вновь повышается на DS.
Рис. 17
|
Такой рост энтропии требует подвода тепла, источником которого являются только тепловые колебания решетки. В результате температура образца понижается (рис. 17). Таким способом удалось достичь температур ниже 0,001 К.
При приближении к абсолютному нулю температур теплоемкость уменьшается до нуля и, следовательно, понижение температуры может быть значительным. Дебай и Джиок предложили применять обратимое адиабатическое размагничивание для понижения температуры образца при приближении к абсолютному нулю. Этот метод стал основным для получения сверхнизких температур.
В качестве парамагнетика используют некоторые парамагнитные соли, например, квасцы, в которые вводят ионы переходных элементов группы железа. Парамагнитная соль помещается в сильное магнитное поле, предварительно охлажденная до гелиевых температур (~ 4,2 К), а затем магнитное поле снимается. Этот метод позволил достичь температур ~ 3×10 -3 К.
|
|
|
Если же вместо электронных использовать “ядерные” парамагнетики, у которых парамагнетизм обусловлен ориентацией магнитных моментов атомных ядер, то можно получить температуры ~10 -5 К.
|
|
|
