 |
Уравнения Максвелла в интегральной форме
|
|
|
|
Лекция 16
УРАВНЕНИЯ МАКСВЕЛЛА
Ток смещения
Явление электромагнитной индукции, открытое Фарадеем, получило дальнейшее развитие в работах Максвелла. Согласно Фарадею явление электромагнитной индукции состоит в возбуждении электрического тока, например, в замкнутом проводнике, который движется в постоянном магнитном поле. Причиной возникновения индукционного тока является сила Лоренца. Как показал Максвелл, причиной возникновения индукционного тока в неподвижном проводнике, находящемся в переменном магнитном поле, является возникшее переменное электрическое поле, которое является вихревым, а не потенциальным в отличие от электростатического поля.
Следовательно, электромагнитная индукция может наблюдаться и тогда, когда в пространстве нет никаких проводников.
В общем случае, при движении проводника в переменном магнитном поле, индукционный ток возбуждается переменным электрическим полем E, т. е. электрической силой F = qeE, и магнитной силой Лоренца.
Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца зависит от выбора системы отсчета.
Идеи Фарадея получили развитие в работах Максвелла, который показал, что существует единое электромагнитное поле, составляющее основу теории классической электродинамики. В основу теории электромагнитного поля положена идея Максвелла о симметрии магнитного и электрического полей. Действительно, согласно теореме о циркуляции вектора 
,
. (1)
Рис. 1
|
Применим эту теорему к электрической цепи, содержащей заряженный плоский конденсатор, который замкнут на внешнее сопротивление (рис. 1). В качестве замкнутого контура L возьмем произвольную кривую, охватывающую провод. На этот контур можно натянуть разные поверхности S и S*. Через поверхность S течет ток проводимости I, а через поверхность S* тока проводимости нет. Ее пронизывает только электрическое поле конденсатора, которое убывает при разряде конденсатора. По теореме Гаусса поток вектора 
сквозь замкнутую поверхность
|
|
|
. (2)
Так как при разряде конденсатора поток вектора изменяется во времени, то 
(3)
Согласно уравнению непрерывности
. (4)
Из уравнений (3) и (4) имеем
, (5)
где слагаемое 
называют плотностью тока смещения.
Сумму 
называют плотностью полного тока.
Согласно (5) линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения (вектор плотности тока смещения и вектор плотности тока проводимости направлены в одну сторону, см. рис. 1).
С введением полного тока циркуляция вектора уже не зависит от выбора поверхности, натянутой на контур L. Поэтому
. (6)
Таким образом, теорему о циркуляции вектора можно обобщить и на случай полного тока, т. е.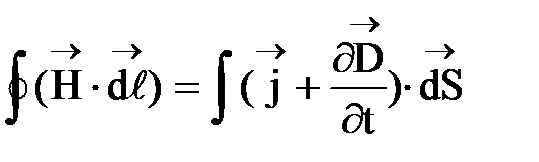 
. (7)
Справедливость данного выражения подтверждена многочисленными экспериментальными данными. В дифференциальной форме закон полного тока записывается в виде
, (8)
где ротор вектора определяется плотностью тока проводимости и плотностью тока смещения.
Замечание: Ток смещения существует лишь там, где изменяется со временем электрическое поле, и нет никаких зарядов.
Как и любой ток, ток смещения создает магнитное поле.
При наличии диэлектрика 
.
Поэтому ток смещения состоит из тока поляризации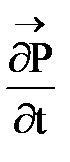 
, вызванного движением связанных зарядов, и тока в вакууме 
, который не связан ни с каким движением зарядов, а целиком обусловлен изменяющимся со временем электрическим полем, возбуждающим переменное магнитное поле.
Уравнения Максвелла в интегральной форме
|
|
|
Открытие тока смещения позволило Максвеллу создать единую теорию электромагнитного поля.
Теория не только объяснила все явления электричества и магнетизма с единой точки зрения, но и предсказала ряд новых явлений, например, что свет - это электромагнитные волны.
Максвеллу удалось составить систему фундаментальных уравнений электродинамики в неподвижных средах.
Рассмотрим систему уравнений Максвелла в интегральной форме.
1. 
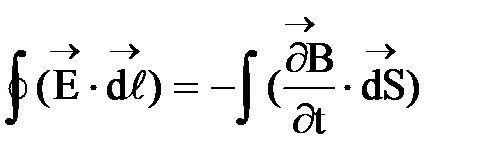. (9)
Циркуляция вектора 
по любому контуру L равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную контуром.
При этом под вектором понимается не только вихревое электрическое поле, но и электростатическое.
Уравнение (9) выражает закон электромагнитной индукции Фарадея.
Переменное магнитное поле возбуждает переменное электрическое поле.
2. 
. (10)
Циркуляция вектора по любому замкнутому контуру L равна полному току через произвольную поверхность, ограниченную контуром.
Вихревое электрическое поле возбуждает вихревое магнитное поле.
Уравнение (10) выражает закон полного тока.
3. 
. (11)
Поток вектора сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью, т. е. выражает теорему Гаусса.
4. 
. (12)
Поток вектора 
сквозь произвольную замкнутую поверхность равен нулю.
Таким образом, уравнения Максвелла описывают единое электромагнитное поле.
Для стационарных полей ( = const, = const) уравнения Максвелла образуют две группы независимых уравнений: для электростатического поля
; (13)
для магнитного поля
. (14)
|
|
|
