 |
П.4 Метод Ньютона (метод касательных).
|
|
|
|

Алгоритм МН:
1) В качестве начального приближения  берем точку, достаточно близкую к точному решению.
берем точку, достаточно близкую к точному решению.
2) В этой точке проводим касательную к графику функций до пересечения с Ох – получаем  и т.д.
и т.д.
3) Процедура повторяется, пока не будет достигнута заданная точность (универсальный критерий прерывания).
Формула метода Ньютона:
уравнение касательной  , находим точку пересечения с Ох
, находим точку пересечения с Ох
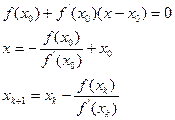
(3.2)
П.5 Скорости сходимости МПД, МХ, МН:
1) Скорость сходимости МПД:
На каждом шаге длина интервала уменьшается вдвое. Таким образом, через k шагов достигается следующая точность -  , решаем неравенство
, решаем неравенство 
Необходимое число шагов: 
То есть, МПД сходится со скоростью геометрической прогрессии со знаменателем ½ (для добавления одного верного десятичного знака – 3 шага).
2) Скорость сходимости МХ:
Теорема 3.1:
Если на интервале [a,b] функция f – непрерывна и дифференцируема, ее производная на этом интервале имеет постоянный знак, т.е. f – либо монотонно убывает, либо монотонно возрастает на всем интервале, то верна следующая оценка:
 (3.3)
(3.3)
где  - решение, найденное на k-ом шаге,
- решение, найденное на k-ом шаге,


Следствие 3.2:
Если  , то если
, то если  (т.е.
(т.е.  ), т.е. универсальный критерий прерывания работает корректно.
), т.е. универсальный критерий прерывания работает корректно.
Теорема 3.3:
Скорость сходимости в МХ не хуже геометрической прогрессии со знаменателем  , а именно имеет следующая оценка
, а именно имеет следующая оценка 
Комментарии:
Если  и
и  очень близки друг к другу, например -
очень близки друг к другу, например -  , то тогда
, то тогда  и скорость сходимости МХ будет выше, чем скорость сходимости МПД.
и скорость сходимости МХ будет выше, чем скорость сходимости МПД.
Итак, выгодно, чтобы  и
и  были близки друг к другу, это будет так, если длина интервала будет стремится к нулю, но в МХ это не так, это происходит в МПД, поэтому выгодно комбинировать МХ и МПД.
были близки друг к другу, это будет так, если длина интервала будет стремится к нулю, но в МХ это не так, это происходит в МПД, поэтому выгодно комбинировать МХ и МПД.
|
|
|
3) Скорость сходимости МН:
Теорема 3.4:
Если функция f(x) дважды непрерывна и дифференцируема на [a,b] и  ,и
,и  на нем не
на нем не
меняет свои знаки, т.е. монотонно возрастает или убывает и при этом не меняет характера выпуклости. Имеет место неравенство:
 (3.4)
(3.4)
 ;
; 
Комментарии:
квадрат обеспечивает удваивание числа верных знаков после каждой итерации.
Таким образом, метод Ньютона работает гораздо быстрее, нежели МПД или МХ.
МН имеет гипергеометрическую скорость сходимости.
Тонкие места МН:
1) Какую из 2-х точек интервала [a,b] выбрать в качестве начального приближения  .
.




В качестве стартовой точки  выгоднее брать точку, в которой знак 2-ой производной совпадает со знаком функции.
выгоднее брать точку, в которой знак 2-ой производной совпадает со знаком функции.
2) В отличие от МПД и МХ – МН сходится не всегда.
 МН может и не сходится(*)
МН может и не сходится(*)
будет сходиться, когда  близко к корню, если
близко к корню, если  выбрано неудачно (далеко от корня) (*).
выбрано неудачно (далеко от корня) (*).
П.6 Многомерный вариант метода Ньютона:
МПД и МХ применимы только для решения НУ, метод Ньютона может быть легко видоизменен, и его можно применять для решения СНУ.
Рассмотрим СНУ n на n (n – уравнений, n – неизвестных):


F(X)=0, X=  .
.
При решении СНУ поступаем таким же образом, как и при решении НУ.
1) Выбираем стартовую точку  , достаточно близкую к корню.
, достаточно близкую к корню.
2)В одномерном варианте мы заменяли функцию на касательную и приравнивали её к нулю. Аналогичным образом поступаем и для функции многих переменных, только там заменяем  на дифференциал, т.е.:
на дифференциал, т.е.:


||

Решаем данное уравнение относительно X:



W – матрица частных производных (матрица Якоби)
умножим на матрицу обратную матрице W слева:
 (3.5)
(3.5)
Окончательный вид формулы многомерного варианта метода Ньютона:

 (3.6)
(3.6)

Замечание:
есть 2 варианта реализации вычисления по формуле (3.6):
а) Явно вычислить обратную матрицу (например, с помощью присоединенной матрицы)
б) Заметим, что вектор  есть ни что иное, как решение СЛАУ
есть ни что иное, как решение СЛАУ
|
|
|
(3.7)  , поэтому мы можем не вычислять обратную матрицу, а только решить СЛАУ (3.7) (например методом Гаусса) и решение этой матрицы подставить в (3.7б)
, поэтому мы можем не вычислять обратную матрицу, а только решить СЛАУ (3.7) (например методом Гаусса) и решение этой матрицы подставить в (3.7б)  .
.
Пример решения СНУ методом Ньютона:

Приводим к виду F(X)=0:


 , в качестве стартовой точки возьмем
, в качестве стартовой точки возьмем 
Сделаем один шаг по многомерному методу Ньютона:





||

Затем находим  и т.д., пока не будет достигнута заданная точность:
и т.д., пока не будет достигнута заданная точность:
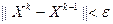
П.7 Вариации метода Ньютона:
7.1 Комбинированный метод (сочетание МН и МХ):
МН быстро сходится, но, увы, не всегда. МХ всегда сходится, но не быстро. Комбинируя оба метода, получаем метод, обладающий достоинствами МХ и МН, а именно – сходится всегда и очень быстро (со скоростью МН).
На каждом шаге КМ проводим и хорду, и касательную, получаем новый интервал.
7.2 Видоизмененный метод Ньютона:
Иногда вычисление производной функции вызывает большие проблемы и чтобы на каждом шаге не вычислять производные, мы вычисляем производную один раз в точке  и используем формулу видоизмененного МН:
и используем формулу видоизмененного МН:
 (3.8)
(3.8)
Видоизмененный МН сходится хуже, чем обычный МН – со скоростью геометрической прогрессии. Эффекта удваивания числа верных знаков после каждой итерации в нем нет.
П.8 Метод итераций, решение НУ и СНУ:
8.1 Одномерный вариант МИ.
Предполагается, что НУ приведено к виду удобному для итераций.
 (3.9)
(3.9)
Запускаем итерационный процесс (3.10):
 (3.10)
(3.10)
Теорема 3.5:
Если итерационный процесс сходится, то сходится к точному решению НУ (3.9), при условии непрерывности функции U.
Доказательство:
в формуле (3.10) переходим к пределу

предел заносим внутрь, используя непрерывность функции U.

Рассмотрим пример решения НУ:
 приводим к виду удобному для итераций, добавим x с обеих сторон:
приводим к виду удобному для итераций, добавим x с обеих сторон:

 процесс зациклился – не сходится
процесс зациклился – не сходится

Попробуем по-другому: перед тем, как прибавить x, разделим на 2.

запускаем итерационный процесс для данной функции U:


данный итерационный процесс сходится к -  .
.
Графическая интерпретация МИ:


итерационный процесс сходится и итерационный процесс расходится
сходится монотонно (рис.1) монотонно (рис.2)


сходится не монотонно, по спирали расходится не монотонно, по спирали
(рис.3) (рис.4)
Заметим закономерности:
1) Если  возрастает, то итерационный процесс всегда ведет себя монотонно, при этом он может и сходится и расходится.
возрастает, то итерационный процесс всегда ведет себя монотонно, при этом он может и сходится и расходится.
|
|
|
Если же  убывает, то итерационный процесс ведёт себя не монотонно, идет по спирали, при этом он может, как сходиться, так и расходиться.
убывает, то итерационный процесс ведёт себя не монотонно, идет по спирали, при этом он может, как сходиться, так и расходиться.
2) Если  то итерационный процесс сходится (рис.1 и рис.3).
то итерационный процесс сходится (рис.1 и рис.3).
Если же  , то итерационный процесс расходится (рис.2 и рис.4)
, то итерационный процесс расходится (рис.2 и рис.4)
Метод итераций может применяться не только для решения НУ, но и для решения СНУ. Все происходит точно так же, т.е. СНУ приводим к виду удобному для итераций.
X – вектор, U – вектор функция.


 (3.10)
(3.10)
Если итерационный процесс (3.10) то он сходится к точному решению -  .
.
Наша задача выяснить условия, при которых итерационный процесс сходится.
Ответ на этот вопрос даёт теорема 3.6.
Теорема 3.6:
Итерационный процесс 3.10 сходится, если отображение U – сжимающее, т.е. для любых
X, Y  (3.11), где С – const, С < 1 (коэффициент сжатия).
(3.11), где С – const, С < 1 (коэффициент сжатия).
Доказательство:

докажем  , при k, l
, при k, l  тем самым покажем, что итерационный процесс сходится.
тем самым покажем, что итерационный процесс сходится.

= (по формуле геометрической прогрессии со знаменателем С)=  =
=

 =
=  , (k, l
, (k, l  )
)
0 0
Как нетрудно заметить, мы попутно оценили скорость сходимости МИ. Сходится со скоростью геометрической прогрессии со знаменателем С, где С – коэффициент сжатия отображения U.
Теперь наша задача научиться оценивать С – коэффициент сжатия. Ответ на этот важный вопрос даёт теорема (3.7)
Теорема 3.7:

Для области D коэффициент сжатия отображения U – максимум нормы матрицы Якоби – матрицы частных производных отображения U.

Таблица сравнительных характеристик методов решения НУ и СНУ:
| МПД | МХ | МН | МИ | |
| Всегда ли работает (сходится) | Да | Да | Нет (сходится, когда  близко к близко к  ) )
| Нет (сходится
 или или  ) )
|
| Скорость сходимости | Геометрическая прогрессия
со знаменате-
лем q=1/2

| Геометрическая прогрессия со знаменателем q=1/2

| Сходится быстрее других методов пос- ле каждой итерации число верных зна-ков удваивается. | Геометрическая прогрессия со знаменателем С, где 
|
| Можно ли решить СНУ многомерным аналогом | Нет | Нет | Да | Да |
| Критерий прерывания | 
| Универсальный критерий прерывания

|
Замечания:
|
|
|
1) На самом деле во всех методах имеется конструктивная оценка скорости сходимости, с помощью которой мы можем вычислить N – необходимое количество шагов. Но на практике пользоваться этими оценками очень не удобно (т.к. приходится находить максимум и минимум производных). Поэтому в 3-х последних методах (МХ, МН, МИ) мы применяем универсальный критерий прерывания.
2)Во всех методах, кроме МН, скорость сходимости есть геометрическая прогрессия, поэтому для достижения одного верного десятичного знака нам потребуется  шагов, где С – знаменатель геометрической прогрессии. МН сходится быстрее, в нем число верных знаков примерно удваивается.
шагов, где С – знаменатель геометрической прогрессии. МН сходится быстрее, в нем число верных знаков примерно удваивается.
Тема 4: Интерполяция.
П.1 Постановка задачи интерполяции, общий подход к её решению:
Пусть имеются точки  (n+1 точка), в которых нам известны значения функции
(n+1 точка), в которых нам известны значения функции  .
.
Задачи интерполяции: научиться вычислять значение функции в любой наперед заданной точке.
Комментарии: интерполяция иногда делится на два вида:
1)  - собственная интерполяция.
- собственная интерполяция.
2)  - экстраполяция.
- экстраполяция.
Геометрическая интерпретация:

Общая идея интерполяции:
Заменяем неизвестную нам функцию f, на некоторую интерполирующую в узлах 
 (т.е.
(т.е.  , которая легко вычисляется, т.е. функция
, которая легко вычисляется, т.е. функция  должна обладать двумя свойствами:
должна обладать двумя свойствами:
1. 
2. g – легко вычисляется в любой наперед заданной точке x.
Для этого поступаем следующим образом:
Фиксируем класс функций N, среди которых будем подбирать искомую функцию g. При этом класс N должен быть достаточно большим, чтобы g нашлась, но с другой стороны – достаточно маленьким, чтобы g была бы там единственной.
В зависимости от класса N интерполируемых функций будем говорить об интерполяции:
а) полиномами
б) сплайнами
в) тригонометрическими функциями
|
|
|


