 |
Центральные формулы для интерполяционного многочлена – формулы Бесселя и Стирлинга.
|
|
|
|
Формулы Ньютона (4.9), (4.10) – односторонние, а Бесселя и Стирлинга – центральные, т.е. в этих формулах, при добавлении новых слагаемых, узлы интерполяции добавляются справа и слева от точки Х, поэтому удобны при практическом вычислении.
В формуле Стирлинга интерполяция проходит по (2n+1) точке:
(x-n,x-n+1,…x0,x1,…xn)
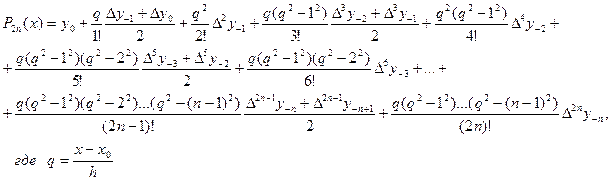
(4.12)
В формуле Бесселя интерполяция проходит по (2n+2) точкам:
(x-n,x-n+1,…x0,x1,…xn,xn+1)
(4.13)
Комментарии:
В формулах Бесселя и Стирлинга слагаемые добавляются попарно, при добавлении новой пары, добавляются два новых узла интерполяции: 1 слева и 1 справа, поэтому вычисления по этим формулам можно обрывать раньше времени.
Сравнительный анализ различных формул вычисления ИМ.
Так происходит интерполяция по 1-ой формуле Ньютона, при добавлении слагаемого, добавляется
1 узел интерполяции (слева направо).
Вторая формула Ньютона добавляется Формула Стирлинга.
по одному узлу – справа налево.
Формула Бесселя. Достоинство всех картинок объединяет в
себе схема Эйткена – в ней узлы интерполяции мы можем добавлять как угодно.
П.3 Интерполяция кубическими сплайнами.
Определение кубического Сплайна.
Кубическим сплайном на сетке x0,x1,…xn называется функция S(х), которая обладает следующими свойствами:
1. на каждом интервале [хi-1, хi], где 1 £ i £ n, функция S(х) является кубическим многочленом (на каждом интервале свой многочлен).
2. на всем интервале [х0, хп] S(х) – дважды непрерывно дифференцируемая функция
3. на краях интервала вторая производная обращается в ноль (краевое условие).
S΄΄(x0)=S΄΄(xn)=0
3’. для периодических кубических сплайнов.
S΄΄(x0)=S΄΄(xn)=0; S΄(x0)=S΄(xn)=0
|
|
|
Исследуем вопрос: любую ли функцию можно проинтерполировать кубическим сплайном и всегда ли это можно сделать единственным образом?
Имеем n участков интерполяции, на каждом – свой кубический многочлен, который задается четырьмя коэффициентами. Итого, имеем 4n коэффициентов, которые нам необходимо найти, для этого нам потребуется столько же уравнений (т.е. 4n. уравнений).
Исходя из условий кубического сплайна:
(подсчет уравнений, которых нам дают условия кубического сплайна)
n участков [хi-1, хi], на границах должны выполнятся условия интерполяции 
; 
- на каждом участке 2 условия, итого получаем 2n условий.
Вспомним второе условие кубического сплайна, т.е. наша функция дважды непрерывно дифференцируема. Внутри участков это, очевидно, выполняется (т.к. 
- кубический многочлен). Необходимо проверить непрерывность S, S’ и S” только лишь на границах интервалов, т.е. рассмотрим точку 
- в ней стыкуются два интервала: [хi-1, хi] и [хi, хi+1]
соответственно кубические сплайны: 
и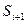 
Предел слева должен быть равен пределу справа для S, S’ и S”, т.е.
- не пишем т.к. оно уже было посчитано в условии интерполяции.
+ два условия из пункта 3. Итого, 4n условий.
Свойства кубического Сплайна
Теорема 4.5:
Среди всех функций, интерполирующих функцию f в точках хi, где 
именно кубический сплайн обладает наименьшей энергией изгиба, т.е. для него достигается минимум интеграла энергии. 
- интеграл энергии.
Следствие 4.6
Из математического анализа известно, что радиус кривизны функции у(х): 
(k(x) – кривизна изгиба). Как известно из физики, энергия изгиба гибкой линейки, принявшей очертание графика функций y(x), вычисляется по формуле: 
- коэффициент жесткости линейки (предположим y’ 
0)
Таким образом, энергия изгиба линейки 
.
Как мы знаем из физики, любая физическая система, в том числе и линейка, стремится минимизировать свою энергию, следовательно, гибкая линейка, пропущенная через точки (хi, уi) , (теорема 4.5) примет очертание кубического сплайна. Отсюда и происходит само слово сплайн (spline – рейка, которую используют чертежники).
|
|
|
Очевидно, что кривизна линейки есть функция непрерывная, следовательно, S, S’ и S” непрерывны – это условие 2 из определения кубического сплайна. Также понятно, что на краях кривизна линейки будет нулевая – отсюда берется условие 3.
|
|
|
