 |
Феррозонды с продольным возбуждением
|
|
|
|
Изобретение феррозондов связывают с именами немецких ученых — Ашенбреннера и Губо [2]. Ими был предложен и опробован феррозонд кольцевого типа (рис. 24).
В качестве сердечника они использовали железную проволоку, покрытую шеллаком. Обмотка возбуждения наматывалась непосредственно на сердечник, измерительная обмотка размещалась на специальном каркасе. Использовался режим работы, при котором измерительная обмотка настраивалась в резонанс на частоту второй гармоники. ЭДС второй гармоники была пропорциональна компоненте поля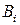 
, действующей в направлении, перпендикулярном к плоскости витков измерительного контура.
|
| Рис. 24. Феррозонд Ашенбреннера и Губо |
Феррозонды Ашенбреннера и Губо были усовершенствованы Ферстером [2], который взамен кольцевого сердечника использовал два раздельных стержневых сердечника. Феррозонд с двумя сердечниками получил наибольшее распространение и применяется до настоящего времени.
Независимо от Ферстера стержневые феррозонды были предложены и опробованы отечественным ученым П.А. Халилеевым [1].
Несмотря на сравнительную давность изобретения феррозондов, цельная и последовательная теория их анализа и расчетов появилась значительно позднее. Основополагающим явилось учение о намагничивании ферромагнитных тел конечных размеров, развитое крупным советским физиком В.К. Аркадьевым. Большой вклад в теорию феррозондов внесли М.А. Розенблат и Р.И. Янус.
Свойства феррозондов с продольным возбуждением рассмотрим на примере дифференциального преобразователя, изображенного на рис.25.
|
| Рис. 25. Дифференциальный феррозонд |
Он содержит два одинаковых сердечника 
, выполненных в виде тонких пермаллоевых пластинок. На каждый сердечник по всей длине с равномерным шагом намотана первичная обмотка 
. Эти две обмотки соединены последовательно, согласно и подключены к источнику синусоидального напряжения звуковой частоты. При этом в сердечниках создаются магнитные потоки, равные по значению и противоположные по фазе. Амплитуда напряженности 
намагничивающего поля выбирается такой, чтобы на участке максимума сердечники входили в насыщение. При полной идентичности обеих половин преобразователя и отсутствии внешнего поля ЭДС, индуцируемая в измерительной обмотке 
, охватывающей оба сердечника, будет равна нулю.
|
|
|
Далее для простоты изложения будем исходить из напряженности магнитного поля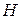 
, помня, что в вакууме (и в воздухе) 
.
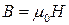Если рассматриваемый преобразователь поместить в постоянное магнитное поле (для простоты изложения предположим, что составляющая вектора 
совпадает с осью сердечников), то в каждый момент времени один из сердечников будет находиться под воздействием суммы напряженностей полей (
), где 
— напряженность переменного поля возбуждения, а второй — под воздействием разности (
). В преобразователе выбран режим работы, для которого 
.
В этом случае можно считать, что в каждом сердечнике происходит приращение напряженности магнитного поля (
). Приращение напряженности в каждом сердечнике вызовет приращение индукции в них в соответствии с зависимостью 
, характерной для материала, из которого изготовлены сердечники. Разлагая зависимость в ряд Тейлора с шагом 
и ограничиваясь тремя членами ряда, получаем
.
Так как магнитные потоки в сердечниках взаимно противоположны, то очевидно, что ЭДС в измерительной обмотке определится их разностью
,
где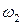 
— число витков измерительной обмотки; 
— площадь поперечного сечения каждого сердечника.
Так как 
— дифференциальная проницаемость, то
|
|
|
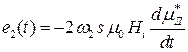, или 
.
Как видно из последнего выражения, обязательным условием функционирования рассматриваемого преобразователя является нелинейный характер зависимости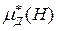 
, т.е. 
.
При синусоидальном поле возбуждения и отсутствии внешнего поля ЭДС в измерительной обмотке, индуцируемые вследствие изменения магнитных потоков отдельно в каждом сердечнике, будут содержать только нечетные гармоники, так как перемагничивание сердечников при этом происходит по симметричным циклам. За счет некоторой неидентичности сердечников и их обмоток имеет место неравенство магнитных потоков. В результате этого в измерительной обмотке возникнет выходная ЭДС, спектр которой будет содержать только нечетные гармоники. Они являются паразитными. Среди этих гармоник преобладающее значение имеет первая гармоника.
При воздействии на преобразователь постоянным полем сердечники будут перемагничиваться по несимметричным циклам. Так как функция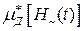 
является четной 
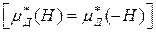, то выходная ЭДС наряду с нечетными (паразитными) гармониками будет содержать и четные. Сумма ЭДС четных гармоник определяет полезный сигнал и однозначно связана с .
Из этой суммы преобладающее значение (при выполнении условия ) имеет вторая гармоника, которую выделяют с помощью полосовых фильтров. При этом стремятся к увеличению частоты поля возбуждения, так как в этом случае абсолютная разность частот первой и второй гармоник увеличивается, что ведет к улучшению качества фильтрации.
Ферромодуляционные преобразователи с продольным возбуждением обладают ориентационной чувствительностью:
, (37)
где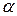 
— угол между вектором напряженности 
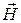и осью сердечника преобразователя (рис. 25).
Из последнего выражения следует, что ЭДС двухстержневого феррозонда с продольным возбуждением пропорциональна скорости изменения относительной дифференциальной проницаемости сердечников.
Если сердечники возбуждаются синусоидальным током, достаточным для их насыщения, то характер изменения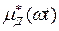 
будет иметь вид, показанный на рис. 26,а. На рис. 26,б показана зависимость 
, из которой видно, что на участке 
эта зависимость не остается постоянной. Пр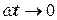и 
и 
величина 
стремится к нулю, при 
, где 
— так называемый угол насыщения сердечников, величина достигает максимального значения. По этой причине форма выходной ЭДС 
, даже при наличии близкого к нулю значения измеряемого поля 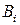(рис. 26,в), как правило, отлична от синусоидальной и имеет вид острых пиков (рис. 26,г).
|
|
|
Ввиду несинусоидального характера выходной ЭДС чувствительность феррозонда может быть оценена по среднему значению выходной ЭДС, пиковому значению или по амплитуде одной из четных гармоник [2].
Учитывая, что функция 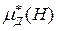— четная, а 
, где — амплитуда поля возбуждения, то при 
получаем:
, (38)
где 
— среднее значение (постоянная составляющая) дифференциальной проницаемости;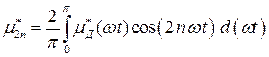 
— амплитуды четных гармоник проницаемости; 
— целые числа.
Подставляя выражение (38) в (37), находим
.
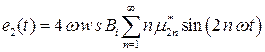Чувствительность феррозонда по любой из четных гармоник будет:
.
Рис. 26. Эпюры работы феррозонда с продольным возбуждением
Заметим, что работа преобразователя во втором режиме имеет ряд преимуществ по сравнению с первым режимом:
− преобразователь является четно-гармоническим, что позволяет отфильтровать полезный сигнал от помех на частоте возбуждения и тем самым существенно уменьшить его порог чувствительности;
− перемагничивание происходит по предельной петле гистерезиса, что улучшает стабильность нуля преобразователя;
− обеспечиваются больший динамический диапазон и более высокая линейность функции преобразования.
|
|
|
