МАЭ. №24. Экзогенная детерминистская теория цикла. Модели Самуэльсона-Хикса и Тевеса.

Модель Самуэльсона-Хикса вкл-ет в себя только рынок благ, и поэтому ур-нь цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен. Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде C_t = C_a,t + C_yy_{t -1}, где C_a - автономное потребление.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде I_t = I_a,t + (y_{t -1} - y_{t -2}).

На рынке благ установится динамическое равновесие, если

(9.1.)

где A_t = С_{a , t} + I_{a , t} .

Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

При фиксированной величине автономных расходов (A_t = A = const) в эк-ке достигается динамическое равновесие, когда объем национального дохода стабилизируется на опр-ом уровне , т.е. y_t = y_{t -1} = y_{t -2} =... = y_t-n = , где n - число периодов с неизменной величиной автономных расходов.

Из уравнения (9.1) следует, что = A /(1 - C_y).

Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.

Освободимся от неоднородности в уравнении (9.1). Значения y_t и удовлетворяют равенству (9.1), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:

(9.2.)

где y_t y_t - .

Т.к. y_t = + ∆ y_t, то направление изменения y_t опр-ся направлением изменения y_t. Из теории решения дифференциальных и конечно-разностных уравнений следует, что характер изменения y_t зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (C_y + )² - 4 , то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.

Если (C_y + )² - 4 > 0, то изменение y_t происходит монотонно; при (C_y + )² - 4 < 0 оно будет колебательным. Следовательно, график функции , изображенный на рис. 1, отделяет множество сочетаний C_y, , обеспечивающих монотонное изменение y_t, от множества комбинаций из значений C_y, , приводящих к колебаниям y_t.

Устремляется ли значение y_t к некоторой конечной величине или уходит в бесконечность, зависит от значения последнего слагаемого характеристического уравнения. Если < 1, то равновесие установится на опр-ом уровне. При > 1 нарушенное 1 раз равновесие больше не восстановится. Когда = 1, тогда значение y_t будет колебаться с постоянной амплитудой.

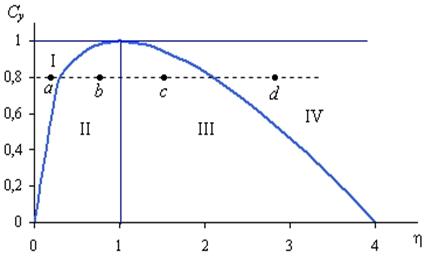
В результате все множество сочетаний C_y и оказалось разделенным на пять областей, как это показано на рис. 1. Если значения C_y и указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение y_t монотонно устремится к новому равновесному уровню:

При значениях C_y и , находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений C_y и , расположенные справа от перпендикуляра, опущенного из точки B на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений C_y, указывают на область III, тогда динамика y_t приобретает характер взрывных колебаний. Комбинации значений C_y, в области IV приводят к тому, что после нарушения равновесия y_t монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания y_t.

В рассматриваемой модели динамика национального дохода в случаях, когда сочетания C_y, соответствуют областям III и IV (см. рис. 1), представляется неправдоподобной: не может в коротком периоде объем производства многократно возрасти или снизится. Это противоречие объясняется тем, что в модели не были учтены два обстоятельства. Во-первых, произведенный национальный доход не может существенно превысить национальный доход полной занятости; этим ограничивается амплитуда колебаний объема национального дохода сверху. Во-вторых, объем отрицательных индуцированных инвестиций не может превысить сумму амортизации; это ограничивает амплитуду колебания национального дохода снизу. В результате, когда сочетания C_y, соответствуют областям III и IV, модель взаимодействия мультипликатора и акселератора принимает вид:

где I_in,t = max{- D; (y_{t -1} - y_{t -2})}, если y_t < y_F, и I_in,t = y_t - C_t - I_a,t при y_t y_F.

С учетом этих обстоятельств приращение автономных инвестиций приводит к колебаниям национального дохода даже при нахождении сочетания C_y, в области IV.

Включим в модель взаимодействия мультипликатора и акселератора еще один фактор - рост населения. Пусть в результате роста населения автономный спрос ежегодно увеличивается в (1 + n) раз. Тогда уравнение (9.1) принимает вид:

В этом случае вследствие мультипликативного эффекта величина равновесного национального дохода ежегодно будет возрастать в (1 + n) раз:

(9.3.)

Первый сомножитель в правой части выражения (9.3) называют супермультипликатором Хикса. Он показывает, насколько увеличивается совокупный спрос в году t, если в дополнение к ежегодному росту автономного спроса, обусловленного ростом населения, на единицу возрастут автономные инвестиции.

Вследствие ежегодного увеличения населения с тем же темпом будут расти автономные расходы и национальный доход полной занятости - верхний предел возможных колебаний национального дохода y_F,t = y_{F, 0}(1 + n) ^t.

Экзогенный рост автономного спроса повышает и нижнюю границу колебаний национального дохода, даже если допустить рост амортизационных отчислений с тем же темпом, что и автономный спрос D_t = D ₀(1 + n) ^t = - I_{n,t, min}. Тогда в ситуациях, соответствующих областям III и IV, после увеличения автономного спроса с темпом (1 + n) колебания национального дохода будут происходить в наклонном коридоре.

Тевес дополнил модель Самуэльсона-Хикса рынком денег, который в соответствии с моделью IS - LM взаимодействует на рынок благ через ставку процента. В используемых нами обозначениях динамическая функция спроса на деньги в модели Тевеса имеет вид:

т.е. в текущем периоде спрос на деньги для сделок зависит от дохода предшествующего периода, а спрос на них как имущество - от текущей ставки процента, что вытекает из предназначения каждой из частей кассовых остатков. Предложение денег задано экзогенно и равно M.

При заданном уровне цен P = 1 на рынке денег установится динамическое равновесие, если:

(9.4.)

Решив равенство (9.4) относительно i_t, получим:

(9.5.)

Из-за того что теперь ставка процента не постоянна, нужно из суммы автономных расходов выделить автономные инвестиции; при этом предполагают, что их объем в текущем периоде зависит от ставки процента предшествующего периода:

Тогда уравнение (9.1) принимает вид:

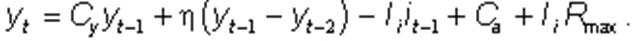(9.6.)

Подставив значение i_{t -1} из уравнения (9.5) в уравнение (9.6), после преобразований получим

(9.7.)

где

Уравнение (9.7) определяет динамику национального дохода после приращения автономных расходов при взаимодействии рынка благ с рынком денег.

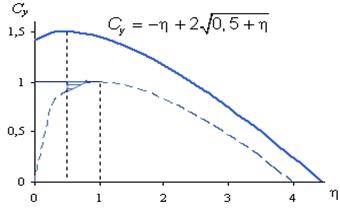
График функции отделяет множество сочетаний C_y, ( + ), приводящих к монотонному изменению объема эффективного спроса, от множества сочетаний этих же параметров, приводящих к его колебаниям. На рис. 2 показана разделительная линия при = 0,5; для сравнения на нем пунктирной линией воспроизведен график, представленный на рис. 1.

Устойчивость или неустойчивость совместного динамического равновесия на рынках благ зависит от значения суммы + . Если + < 1, то равновесие устойчиво, при + > 1 после нарушения равновесия оно не восстановится, а при + = 1 экзогенный толчок в виде приращения автономного спроса приведет к равномерным незатухающим колебаниям эффективного спроса около своего равновесного значения. Поскольку по своей природе величина положительная, то теперь разделительная линия проходит выше, чем в модели Самуэльсона-Хикса. Но из-за того, что предельная склонность к потреблению не может превышать единицу, все точки, лежащие выше линии C_y = 1, не имеют эк. смысла. Как следует из рис. 2, с включением в модель рынка денег область устойчивого равновесия сокращается на заштрихованную площадь; это уменьшение тем больше, чем выше .

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: