Спрос на деньги. Концептуальные подходы к обоснованию функции спроса на деньги.

Под спросом на деньги понимается стремление населения, фирм, государства сохранить часть активов в ликвидной форме или в фор­ме денежных запасов. Спрос на деньги вытекает из двух функций:

1) ср-ва обращ-я (спрос для использ-я денег в разл-х сделках), 2) ср-ва сохр-я богатства.

Существует несколько концепций, по-разному трактующих спрос на деньги. Сторонники классической теории связывали спрос на день­ги с тем, что деньги необходимы для покупки товаров и услуг в буду­щем, и что такая потребность возникает в связи с временным разры­вом между получением денег и их расходованием. Согласно данной концепции, спрос на деньги определяется из формулы количественной теории: M x V = P x Y Если денежную массу заменить на Мd— величину спроса на деньги, то получим, что спрос на номинальное количество денег будет равен Мd = P Y / V Отсюда спрос на деньги зависит от 1) абсолютного уровня цен, 2) объе­ма производства, 3) скорости обращения денег, который, в свою очередь, предопределяется величиной ставки процента.

Спрос на деньги может быть выражен также следующей формулой: Мd = L = k p y, где k — коэффициент, характеризующий наличность, остающуюся в среднем за период на руках у населения в форме кассовых остатков. Коэффициент k есть величина, обратная скорости обращения денег (k = 1/ V). Т. О., спрос на номинальное количество денег может быть представлен L = 1/ V x р у, а спрос на реальные кассовые остатки равен

Мd / р = 1/ V x у.

В данных концепциях представлена трактовка трансакционного спроса на деньги, являющегося функцией от дохода: LTP = LTP(y+). Кейнсианская концепция спроса на деньги наряду с трансакционным спросом выделяет спекулятивный спрос на деньги. Разделяя по­зицию классиков о формировании трансакционного спроса на деньги, Кейнс выделил два мотива в составе данного спроса: 1) спрос на день­ги для сделок запланированного характера; 2) спрос на деньги для со­вершения незапланированных сделок (мотив предосторожности). Из функции денег, как средства сбережения, Кейнс выводит спеку­лятивный спрос. Сбережения (S) могут распадаться на прирост: 1) об­лигаций (DВ), 2) денег (DM), т. е. S = (DВ) + (DМ).

Решая вопрос о спросе на деньги как средстве обращения, населе­ние определяет наиболее выгодную альтернативу: 1) купить облигации и получать доход в виде процента;

2) оставить сбережения в денежной форме, которая является абсо­лютно ликвидной, но не приносит дохода.

Именно хранение части портфеля активов в виде денег для приоб­ретения облигаций Кейнс назвал спекулятивным спросом. Спекуля­тивный спрос отражает обратную связь между величиной спроса на деньги и нормой ссудного процента: Мd = L(y,I)

Спекулятивный спрос связан с функцией сохранения ценностей. За это субъект должен заплатить потерей дохода от альтернативных ви­дов имущества. Поэтому спрос на деньги как имущество обратно про­порционален доходности ценных бумаг.

Сумма, за которую можно купить новую акцию, обеспечивающую такой доход, как ранее выпущенная, можно определить

B = iн x Bн/i, где Вн — номинальная стоимость облигации; i — твердый процент, выплачиваемый на облигацию; iн — текущая ставка процента, характеризующая доходность вновь выпускаемой облигации; В — текущий рыночный курс ранее выпущенной облигации. Тогда рыночный курс в будущем будет равен Be = iн x Bн/ie то ожидаемые потери примут вид: B – Be = iн x Bн/i – iн x Bн/ie

Эту потерю экономический субъект сопоставляет с гарантирован­ным доходом на облигацию и сохраняет ее до тех пор, пока iн x Bн ≥ iн x Bн/i – iн x Bн/ie или 1>1/i – 1/ ie

Величина ставки процента, при которой неравенство превращается в равенство, называется критической процентной ставкой (ik) и выра­жается: ik = ie /(1 + ie).

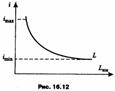
Спрос на деньги как имущество (рис. 16.12): LИМ = Li (imax – i)

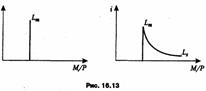
Совокупный спрос на деньги равен сумме трансакционного спроса (LT) и спекулятивного спроса (LS) (рис. 16.13).

Таким образом, величина спроса на деньги зависит от:

1) дохода (прямая зависимость — трансакционный спрос); 2) процентной ставки (обратная зависимость — спекулятивный спрос); 3) к — величины обратной скорости обращения денег. Функция спро­са на деньги может быть представлена:

M/P = L(y, i, Cp) где Ср — средние затраты на обращ-е других форм богатств в день­ги.

Иной концепции придерживаются монетаристы, считающие что экономические субъекты формируют такой состав портфеля своих ак­тивов, который позволяет при данном объеме совокупных активов максимально удовлетворять полезность от владения имуществом, т. е. спрос на деньги рассматривается как оптимизация портфеля акти­вов. В состав портфеля включаются: 1) облигации, 2) акции, 3) деньги. Задача состоит в оптимизации структуры активов при каждом их данном объеме, чтобы обеспечить желаемый уровень дохода при мини­мальном риске r* = Σαi x ri, где r* — желаемый уровень доходности; Li — доля активов данного вида; ri. — доходность данного вида.

R (риск) определяется как вероятность отклонения дохода от ожи­даемого дохода. Отсюда функция спроса на деньги может быть выра­жена: L = f (rB, rA, Пe, W), где rB — доходность облигаций; rA — доходность акций; Пe — доход денег, равный темпу инфляции; W — общий объем активов.

Своеобразие монетаристской концепции состоит в том, что они счи­тают, что деньги являются наихудшим видом активов, доходность по которым определяется ожидаемым темпом инфляции, который может быть отрицательным, объясняют спрос на деньги, приносящий доход, то есть рассматривают агрегаты М2, М3 не объясняя специфику М1.