 |
Результаты моделирования процесса теплопроводности, полученные по неявной схеме (7.59)
|
|
|
|
 x
t
| |||||
| 3,000 | 4.500 | 5,000 | 4,500 | 3,000 | |
| 3,000 | 4,000 | 4,428 | 4,000 | 3,000 | |
| 3,000 | 3,688 | 3,975 | 3,688 | 3,000 | |
| 3,000 | 3,476 | 3,669 | 3,476 | 3,000 | |
| 3,000 | 3,325 | 3,461 | 3,325 | 3,000 | |
| 3,000 | 3,225 | 3,316 | 3,225 | 3,000 | |
| 3,000 | 3,154 | 3,218 | 3,154 | 3,000 | |
| 3,000 | 3,106 | 3,150 | 3,106 | 3,000 | |
| 3,000 | 3,073 | 3,103 | 3,073 | 3,000 | |
| 3,000 | 3,050 | 3,071 | 3,050 | 3,000 | |
| 3,000 | 3,034 | 3,049 | 3,034 | 3,000 |
На рис. 7.36 представлена графическая иллюстрация результатов расчетов.
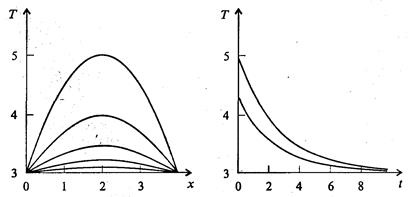
Рис. 7.36. Графики зависимости температуры от координаты в разные моменты времени (сверху вниз t = 0, t = 2, t = 4, t = 6, t = 8), в начальный момент времени температура самая высокая, затем она постепенно выравнивается, и зависимости температуры от времени в разных точках стержня. Верхняя кривая соответствует x = 2; ниже - x = 1 и х = 3; прямая линия, совпадающая здесь с осью абсцисс, - значение температуры на концах стержня
Ясно, что по мере эволюции во времени температура стержнябудет выравниваться и асимптотически стремиться к 3o С во всех точках.
Контрольные вопросы и задания
1 Какие причины обусловливают особую значимость компьютерного моделирования в физике?
2. Какие аналогии проводятся между реальным и компьютерным экспериментами?
3. Почему при исследовании реальныхпроцессов движения тел нужна дифференциальная форма законов Ньютона?
4. Как зависит сила сопротивления от скорости движущегося тела?
5. Какая из составляющих силы сопротивления - линейная или квадратичная - будет доминировать при погружении в воду полого стального шара - батискафа диаметром 2 м и с толщиной стенки 1 см при достижении им постоянной скорости погружения?
6. Почему учет силы сопротивления среды делает многие, известные из школьного курса физики модели, более реалистичными? Приведите примеры таких моделей.
|
|
|
7. Как надо преобразовать формулировку содержательной задачи, прежде чем приступать к ее решению?
8. Как можно отобразить результаты моделирования в задаче о свободном падении тела в наиболее удобной для восприятия форме?
9. В чем преимущества и недостатки моделирования с помощью составления программ и с использованием табличных процессоров?
10. Разработайте программу для ЭВМ, используя одиниз методов численного интегрирования системы дифференциальных уравнений, позволяющую моделировать падение тела с учетом сопротивления среды. Предусмотрите интерактивный интерфейс для ввода данных, выбора формы представления результатов и т.д.
Решите с помощью этой программы одну из следующих задач:
а) с высоты Н падает предмет, через время t он оказывается на земле, требуется определить, с какой скоростью приземлится предмет;
б) металлический шарик падает в воде и в глицерине,провести сравнение результатов моделирования;
в) определить момент встречи (высоту и время) тела массы т1 свободно падающего с высоты Н0, и тела массы т2, брошенного вертикально вверх с достаточно большой начальной скоростью.
11. Какова траектория движения тела, брошенного под углом к горизонту, при отсутствии сопротивления среды? Как меняется эта траектория качественно при наличии сильного сопротивления?
12. Для чего производится обезразмеривание величин, характеризующих движение? Возможен ли з рассматриваемой задаче другой способ обезразмеривания?
13. Сделайте сравнительный анализ характеристик движения тела, брошенного под углом к горизонту, с учетом и без учета сопротивления воздуха. Как они будут изменяться с увеличением начальной скорости?
14. Разработайте программы решения задач:
а) при построении модели полета тела, брошенного под углом к горизонту, поверхность Земли считалась плоской, учтите в математической моделикривизнуЗемли, проведите соответствующее моделирование.
|
|
|
б) произведите моделирование полета тела, брошенного под углом к горизонту на Луне, проведите сравнение с результатами моделирования для Земли при аналогичных начальных условиях;
в) задача о подводной охоте: на расстоянии т под углом а подводный охотник видит неподвижную акулу, на сколько метров выше ее надо целиться, чтобы гарпун попал в цель? как будет выглядеть постановка и решение этой задачи, если акула движется? произведите соответствующее моделирование.
15. В чем могут заключаться усовершенствования приведенной выше модели взлета ракеты?
16. Насколько в действительности хороша аппроксимация, принятая для зависимости силы сопротивления от скорости, при очень больших скоростях?
17. Найдите в специальной литературе данные о характере зависимости силы сопротивления от скорости движения при скоростях порядка скорости звука и больших и внесите усовершенствования в модель.
18. Запишите математическую модель для движения двухступенчатой ракеты.
19. Проведите исследование на тему: с каким минимальным запасом топлива некоторая ракета может вывести на орбиту спутник? Все необходимые параметры задайте правдоподобными самостоятельно.
20. Какой может быть траектория космического аппарата, запускаемого сЗемли,относительно нее, если пренебречь влиянием других небесных тел? Чем определяется эта траектория?
21. Как будут выглядеть уравнения движения в системеЗемля - Луна - малоенебесное тело, если пренебречь влиянием Солнца-и других планет?
22. Составьте программу моделирования движения малого космического тела. Получите с помощью этой программы круговую орбиту. Экспериментально подберите безразмерные начальные условия для получения всех видов орбит: эллиптических, параболических, гиперболических. Для эллиптических орбит вычислите длину большой полуоси, эксцентриситет, период обращения.
23. Проверьте в ходе моделирования второй закон Кеплера дляэллиптическихорбит.
24. Проверьте в ходе моделирования третий закон Кеплера для эллиптических орбит.
25. Уточните модель, учитывая действие на спутник, движущийся вокруг Земли, помимо силы притяжения Земли, слабой постояннойсилы W, обусловленной «солнечным ветром».
|
|
|
26. Есть ли качественные различия в задачах о взаимном движении двух небесных тел и двух заряженных частиц, и чем они обусловлены?
27. Произведите моделирование движения тела массы т, несущего заряд q, поддействием электростатических сил, создаваемых произвольно расположенной группой тел с зарядами Q1, Q2,..., Qn (все они - в одной плоскости).
28. Как выглядит первая нелинейная поправка при переходе от полного уравнения свободных колебаний к уравнению малых колебаний?
29. Какое периодическое движение называют гармоническим?
30. Как выглядит в общем случае формула гармонического разложения периодической функции (разложения в ряд Фурье)?
31. Какие качественные изменения вносит учет трения при анализе движения маятника?
32. С какой частотой происходят вынужденные колебания при наличии гармонической вынуждающей силы?
33. В чем состоит особенность параметрического возбуждение колебательного движения?
34. Изучите в ходе компьютерного моделирования зависимость периода колебаний математического маятника от их амплитуды. Изобразите эту зависимость графически в диапазоне амплитуд 0 < θ < π. Выполните спектральное разложение колебаний для амплитуд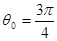 
,0,9 π, выделив 3-5 гармоник.
35. Изучите с помощью компьютерного моделирования колебания пружинного маятника, движущегося под влиянием упругой силы F = -ах-bх3, где х - смещение из положения равновесия.
Слагаемое (-ах) связано с законом Гука и доминирует при малых х (область упругих деформаций), слагаемое (-bх3) - нелинейный член силы упругости, доминирующий при больших x. Изучение может включать те же элементы, которые описаны для математического маятника.
36. «Постоянной времени» τ0 колебательной системы с затуханием называется промежуток времени, за который начальная амплитуда уменьшится в е раз. Для линейной системы она равна 
Определите с помощью компьютерного моделирования постоянную времени для затухающих нелинейных колебаний, ее зависимость от начальной амплитуды.
|
|
|
37. Относительно каких процессов атмосферу можно рассматривать как сплошную газовую среду и относительно каких - нельзя?
38. Какие примеры сплошных сред и соответствующих процессов вам известны?
39. Как в общем случае связаны потенциал и напряженность электростатического поля?
40. Что такое эквипотенциальная поверхность? силовая линия?
41. Какие изменения и дополнения следует внести в приведенную выше программу, чтобы она позволила строить трехмерные эквипотенциальные поверхности? их сечения произвольными плоскостями?
42. Реализуйте программу построения силовых линий электростатическогополя, создаваемого системой точечных зарядов.
43. Разработайте компьютерную модель, позволяющую строить изолинии поля, создаваемого совокупностью заряженных пластин и точечных зарядов. Создайте с ее помощью изображение
а) поля в плоском конденсаторе;
б) поля, создаваемого пластинами, стоящими под углом друг к другу.
44. В чем заключается процесс теплопроводности, и какие физическиемеханизмы его поддерживают на молекулярном уровне?
45. Как выглядит уравнение теплопроводности в двумерномслучае?
46. В чем заключаются начальные и краевые условия в задаче теплопроводности?
47. Как выглядит конечно-разностная аппроксимация первой производнойповремени? по пространству? В чем различие этих аппроксимаций для внутренних и граничных узлов сетки?
48. В чем заключаются устойчивость и эффективность численного метода решения краевых задач?
49. В чем состоит принципиальная разница между явной и неявнойсхемами конечно-разностного решения дифференциальных уравнений?
50. Получите результаты, приведенные выше в примерах моделирования процесса теплопроводности, постройте соответствующие графики. Как еще можно представить результаты расчетов?
51. Выясните, как в рассмотренных примерах моделирования процесса теплопроводности будут изменяться результаты расчетов при уменьшении (увеличении) параметра a.
52. Какими величинами можно обезразмерить переменные в рассмотренных выше примерах моделирования процесса теплопроводности? Проведите обезразмеривание в одном из них для явной и неявной схем.
53. Проведите моделирование теплопроводности, когда начальные условия заданы функцией
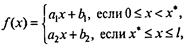
где х* - некоторая точка стержня.
|
|
|
