Главная | Обратная связь | Поможем написать вашу работу!

Нормальный делитель группы. Фактор-группа

Смежные классы. Разложение группы по подгруппе

Пусть – группа, – ее подгруппа, – произвольный элемент группы . Составим множество . Это непустое множество, называется левым смежным классом группы по подгруппе , определяемым элементом . Множество называется правым смежным классом группы по подгруппе , определяемым элементом . В общем случае .

Задача 61. В найти правый и левый смежные классы, определяе-мые элементом , если подгруппа .

Решение.

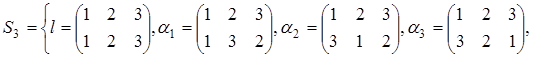
Составим классы

Заметим, .

Пусть – группа и – ее подгруппа.

Если , то говорят, что группа по подгруппе разложена на один смежный класс.

Если , то в существует элемент и тогда составим класс .

Если , то говорят, что группа по подгруппе разложена на два левых смежных класса .

Если , то имеем разложение группы на три смежных класса по подгруппе и т. д.

Процесс разложения группы по подгруппе на левые смежные классы может быть конечным, может быть бесконечным.

Аналогично можно получить разложение группы по подгруппе на правые смежные классы: .

Правое разложение не обязано совпадать с левым разложением.

В результате мы получаем два множества классов:

и – левое и правое фактор-множества множества по подмножеству . Длина этих множеств называется индексом подгруппы в группе .

Задача 62. Найти фактор-множество множества по подгруппе относительно операции сложения.

Решение. Операция сложения в коммутативная, поэтому левое и правое разложения по будут одинаковые. Разложим на на левые смежные классы.

, например, . Строим . . Имеем разложение по на два смежных класса. Фактор-множество: .

Задача 63. В мультипликативной группе

, , , , , возьмем подгруппу . Найти фактор-множество множества по .

Решение. При левостороннем разложении по имеем:

, , , т. е. левосторонний фактор-множество .

При правостороннем разложении по имеем:

, , , т. е. правостороннее фак-тор-множество , причем , .

Индекс подгруппы в равен 3.

Задача 64. Найти разложение аддитивной группы по подгруппе целых чисел, кратных 3.

Решение. .

, например, . Составим . Следовательно, класс состоит из всех целых чисел, которые при делении на 3 дают в остатке 1. , напри-мер, , . Составим . Следовательно, класс состоит из всех целых чисел, которые при делении на 3 дают в остатке 2. Итак, в находятся все целые числа, которые при делении на 3 дают в остатке 0, в классе – все целые числа, которые делятся на 3 дают в остатке 1, в классе – все числа с остатком 2. Но при делении на 3 возможны только остатки 0, 1, 2. Значит, все целые числа распределились по классам , т. е. разложение на смежные классы по имеет вид: . Так как сложение в коммутативное, то левостороннее разложение совпадает с правосторонним. Индекс подгруппы в равен 3.

Нормальный делитель группы. Фактор-группа

Если в группе относительно подгруппы при любом элементе , т. е. если любой элемент группы перестановочен с подгруппой , то подгруппа называется нормальным делителем группы .

Если операция в группе коммутативна, то любая подгруппа в группе является нормальным делителем. Если при левостороннем и при правостороннем разложении группы по подгруппе смежные классы, на которые распадается группа , получаются одинаковыми, то – нормальный делитель группы . Верно и обратное: если – нормальный делитель в группе , то при левостороннем и при правостороннем разложении группы по подгруппе смежные классы, на которые распадается группа , получаются одинаковыми.

является нормальным делителем группы тогда и только тогда, когда при любом и любом элемент .

Задача 65. Если индекс подгруппы группы равен 2, то – нормальный делитель группы .

Решение. Если подгруппа имеет индекс 2 в группе , то , где и , т. е. . Следовательно, классы смежности левостороннего разложения совпадают с соответствующими классами правостороннего разложения, т. е. – нормальный делитель группы .

Задача 66. Будет ли группа в задаче 63 нормальным делителем в группе ?

Решение. Левостороннее разложение группы по подгруппе состоит из классов , и . Правостороннее разложение состоит из классов , , , но , , т. е. подгруппа не является нормальным делителем группы .

Задача 67. Найти фактор-группу группы по подгруппе всех чисел, кратных 3.

Решение. Так как сложение в коммутативно, то – нормальный делитель. Найдем разложение по : . Фактор-множество состоит из классов . Зададим на операцию сложения:

Заполнение таблицы Кэли осуществляется по правилу:

Например, . Это множество состоит из всех целых чисел , где , т. е. , . Тогда . Итак, мы получили фактор-группу , операция сложения в которой задана вышеука-занной таблицей Кэли.

Задача 68. Найти фактор-группу группы по подгруппе .

Решение. – нормальный делитель, т. к. сложение в коммутативно. Найдем разложение по : . Действительно, изобразим на числовой оси, а элементы отметим на ней точками:

Построим , где . Если , то , если , то элементы отметим звездочками. Тогда состоит из элементов, отмеченных точками и звездочками. В это множество не попадает элемент, например, . Тогда строим множество , элементы которого обозначим штрихом. Тогда состоит из элементов, обозначенных точками, звездочками и штрихами, но не совпадает с . Очевидно, чтобы совпало с , необходимо, чтобы .