 |
Гомоморфизм и изоморфизм групп
|
|
|
|
Гомоморфизмом группы  в группу
в группу  называется такое отображение
называется такое отображение  множества
множества  и в множество
и в множество  , при котором композиция любых двух элементов
, при котором композиция любых двух элементов  и
и  относительно операции
относительно операции  отображается в композицию образов элементов
отображается в композицию образов элементов  и
и  относительно операции
относительно операции  , т. е.
, т. е.  . При гомоморфизме групп: 1) нейтральный элемент
. При гомоморфизме групп: 1) нейтральный элемент  группы
группы  отображается в нейтральный элемент
отображается в нейтральный элемент  группы
группы  , т. е.
, т. е.  . 2) пара симметричных элементов
. 2) пара симметричных элементов  ,
,  группы
группы  отображаются в пару симметричных элементов
отображаются в пару симметричных элементов  ,
,  группы
группы  .
.
Множество всех элементов группы  , которые при гомоморфизме
, которые при гомоморфизме  отображаются в нейтральный элемент
отображаются в нейтральный элемент  группы
группы  относительно сужений операции
относительно сужений операции  образует подгруппу группы
образует подгруппу группы  , которая является нормальным делителем группы
, которая является нормальным делителем группы  и называется ядром гомоморфизма
и называется ядром гомоморфизма  .
.
Задача 69. Определить, является ли отображение  гомоморфизмом группы
гомоморфизмом группы  в группу
в группу  . Если «да», то найти
. Если «да», то найти  .
.
Решение.  .
.
При отображении  возможны следующие случаи:
возможны следующие случаи:
1)  – чет,
– чет,  – чет; 2)
– чет; 2)  – нечет,
– нечет,  – чет; 3)
– чет; 3)  – чет,
– чет,  – нечет; 4)
– нечет; 4)  – нечет,
– нечет,  – нечет. Проверим, как ведут себя
– нечет. Проверим, как ведут себя  . В первом случае
. В первом случае  – чет, следовательно
– чет, следовательно  . Но
. Но  ,
,  , т. к.
, т. к.  и
и  – четные. Тогда
– четные. Тогда 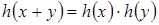 . Во втором случае
. Во втором случае  – нечетные, следовательно
– нечетные, следовательно  . Но
. Но  ,
,  и
и  , т. е.
, т. е. 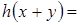
 . В третьем случае
. В третьем случае  ,
,  ,
,  , т. е.
, т. е. 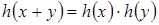 . В четвертом случае
. В четвертом случае  ,
,  ,
,  , т. е.
, т. е. 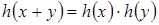 . В итоге можно сказать, что для любых
. В итоге можно сказать, что для любых  верно:
верно: 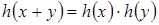 . Следовательно,
. Следовательно,  – гомоморфизм группы
– гомоморфизм группы  в группу
в группу  .
.
Ядром гомоморфизма  является множество всех четных чисел, т. е.
является множество всех четных чисел, т. е.  .
.
Если при гомоморфизме  отображение
отображение  взаимооднозначно, т. е.
взаимооднозначно, т. е.  , то
, то  называется изоморфизмом группы
называется изоморфизмом группы  в группу
в группу  . Если при этом имеется наложение множества
. Если при этом имеется наложение множества  на множество
на множество  , то группы
, то группы  и
и  называются изоморфными.
называются изоморфными.
Задача 70. Изоморфны ли группа  и мультипликативная группа кольца
и мультипликативная группа кольца  ?
?
Решение.  .
.  – множество обратимых элементов из
– множество обратимых элементов из  . Взаимооднозначных отображений
. Взаимооднозначных отображений  на
на  несколько. Из них надо выбрать то (если оно существует), которое удовлетворяет определению изоморфного отображения. Для удобства рассуждений построим таблицы Кэли для
несколько. Из них надо выбрать то (если оно существует), которое удовлетворяет определению изоморфного отображения. Для удобства рассуждений построим таблицы Кэли для  и
и  :
:
|
|
|
 : :
| 
| 
| 
|  : :
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |||

| 
| 
| 
| 
| 
|
Зададим такое отображение  , при котором нейтральный эле-мент
, при котором нейтральный эле-мент  отобразится в нейтральный элемент
отобразится в нейтральный элемент  (по свойству изоморфиз-ма), т. е.
(по свойству изоморфиз-ма), т. е.  . Тогда остается только одна возможность для отображения
. Тогда остается только одна возможность для отображения  . Итак,
. Итак,
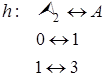 .
.
Проверим, будет ли верно: 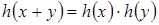 при
при  .
.

|
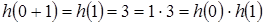
|

|
 , т. к. , т. к.  по по  . .
|
Итак, 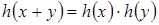 при
при  , т. е.
, т. е.  – изоморфизм. Следова-тельно, группа
– изоморфизм. Следова-тельно, группа  и мультипликативная группа кольца
и мультипликативная группа кольца  – изоморф-ны.
– изоморф-ны.
Задача 71. Доказать изоморфизм групп  и
и 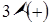 .
.
Решение. 1 способ. Отображение
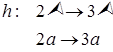
взаимооднозначным отображением  на
на  . Действительно,
. Действительно,  влечет
влечет  , отсюда
, отсюда  . Любое целое число вида
. Любое целое число вида  имеет прообраз, а именно:
имеет прообраз, а именно:  . При этом отображение
. При этом отображение 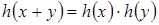 , т. к.
, т. к.  ,
,  ,
,  . Следовательно,
. Следовательно,  – изоморфизм
– изоморфизм 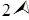 и
и  .
.
Изоморфизм колец. Гомоморфизм колец
Кольца  и
и  называются изоморфными, если можно установить такое отображение
называются изоморфными, если можно установить такое отображение  , при котором для
, при котором для 
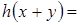
 и
и  .
.
Задача 72. Доказать, что кольцо вещественных квадратных матриц
 -го порядка изоморфно кольцу линейных операторов
-го порядка изоморфно кольцу линейных операторов  -мерного линейного пространства
-мерного линейного пространства  относительно фиксированного базиса
относительно фиксированного базиса  .
.
Решение. Пусть  – кольцо квадратных матриц
– кольцо квадратных матриц  -го порядка с вещественными элементами,
-го порядка с вещественными элементами,  – кольцо линейных операторов
– кольцо линейных операторов  -мерного пространства
-мерного пространства  над полем
над полем  . Возьмем произвольный линейный оператор
. Возьмем произвольный линейный оператор  и рассмотрим его матрицу
и рассмотрим его матрицу  относительно базиса
относительно базиса  :
:
 , ,
| где  – координатный столбец вектора – координатный столбец вектора  в базисе в базисе  , ,
|
 – координатный столбец вектора – координатный столбец вектора 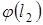 в базисе в базисе  , ,
| |
 – координатный столбец вектора – координатный столбец вектора  в базисе в базисе  . .
|
Так как координаты вектора в заданном базисе определяются однозначно, то для оператора  в базисе
в базисе  матрица
матрица  определена однозначно.
определена однозначно.
Обратно, пусть дана произвольная матрица
 .
.
Можно ли считать ее матрицей некоторого оператора  в базисе
в базисе  и есть ли еще оператор
и есть ли еще оператор  , для которого матрицей в базисе
, для которого матрицей в базисе  будет та же матрица
будет та же матрица  ?
?
|
|
|
Построим векторы 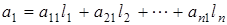 ,
, 
 , ….,
, ….,  . Существует линейный оператор
. Существует линейный оператор  такой, что
такой, что  ,
,  ,…,
,…,  . Это оператор
. Это оператор  .
.
 . Этот оператор линейный, так как
. Этот оператор линейный, так как  и
и  , где
, где  ,
,  . Этот оператор
. Этот оператор  имеет своей матрицей в базисе
имеет своей матрицей в базисе  матрицу
матрицу
|
|
|


