 |
Задание 4. Решение системы линейных алгебраических уравнений (СЛАУ)
|
|
|
|
СЛАУ можно записать в матричном виде
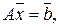
где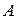 
– матрица коэффициентов при неизвестных; 
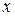– вектор неизвестных; 
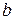– вектор свободных членов.
При решении СЛАУ можно использовать метод обратной матрицы. Тогда решение можно найти по формуле:
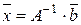(3)
Пример. В Варианте 6 приведен следующий пример:
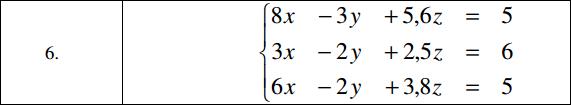
Файл-сценарий для Задания 4 приведен на Рис 10.
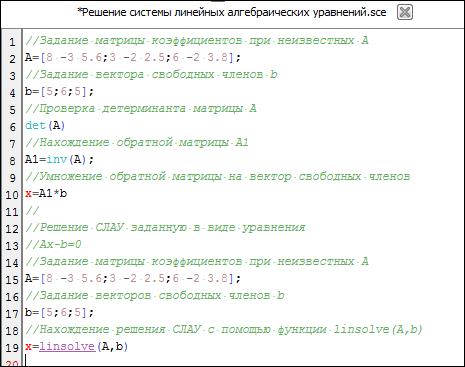
Рис 10- Файл-сценарий решения СЛАУ. Задание 4
Решение СЛАУ приведено на Рис 11.
Рис 11- Решение СЛАУ. Задание 4
Задание 5. Численное интегрирование
Рассчитать значение определенного интеграла можно с помощью формулы Ньютона-Лейбница
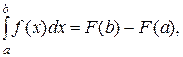(4)
где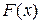 
– первообразная подинтегральной функции.
Сложность заключается в том, что не всегда можно найти первообразную подинтегральной функции, или она оказывается слишком сложной. В этих случаях для вычисления интеграла используют различные численные методы.
В функциях интегрирования в Scilab реализованы различные численные алгоритмы. Наиболее универсальной командой интегрирования в Scilab является
 |
[I, err] = intg(a, b, name [,er1 [,er2]]),
где name — имя функции, задающей подынтегральное выражение (функция может быть задана в виде набора дискретных точек, т.е. таблицей или с помощью внешней функции);
а и b – пределы интегрирования;
er1 и еr2 — абсолютная и относительная точность вычислений (необязательные параметры).
Пример. В Варианте 6 приведен следующий пример:
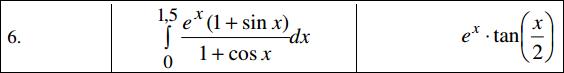
Файл-сценарий выполнения Задания 5 приведен на Рис 12
Рис 12- Файл-сценарий Задания 5. Численное интегрирование
Решение определенного интеграла представлено на Рис 13
Рис 13- Решение Задания 5. Численное интегрирование
Задание 6. Аппроксимация экспериментальных данных методом наименьших квадратов
|
|
|
Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.
Идея метода наименьших квадратов заключается в том, что функцию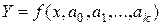 
необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений 
от расчетных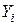 
была наименьшей
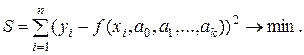(5)
Задача сводится к определению коэффициентов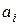 
из условия (5).
Для реализации этой задачи в Scilab предусмотрена функция
[a,S] = datafit(F,z,c),
где F – аппроксимирующая функция, параметры которой необходимо подобрать; z – матрица исходных данных; с – вектор начальных приближений; а – вектор коэффициентов; S – сумма квадратов отклонений измеренных значений от расчетных.
Вид аппроксимирующей функции, подбирается как наиболее подходящий для заданных экспериментальных данных, это может быть:
- Линейная,
- Логарифмическая,
- Полиномиальная,
- Экспоненциальная и др.
Чаще в качестве аппроксимирующей функции выбирают полином необходимой степени.
Пример. В Варианте 6 приведены следующие данные для аппроксимации:
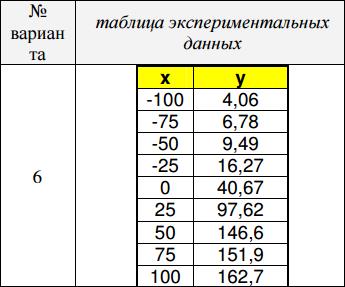
Файл-сценарий для выполнения Задания 6 приведен на Рис 14
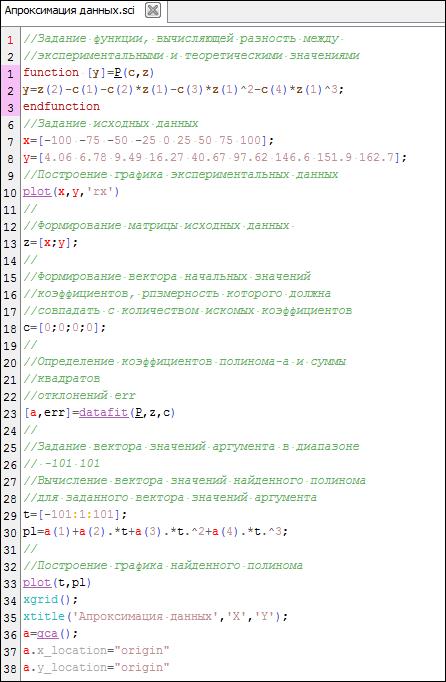
Рис 14- Задание 6. Аппроксимация данных
График полинома представлен на Рис 15
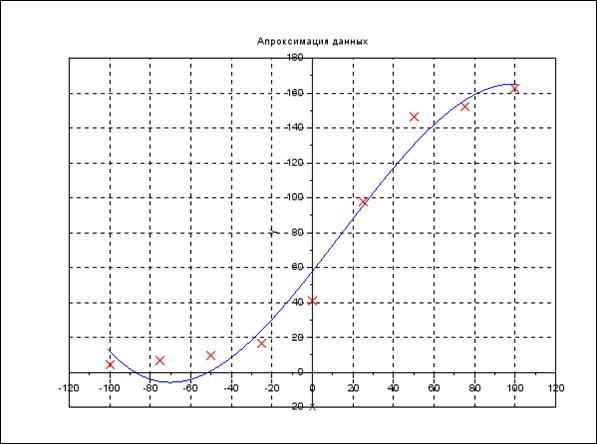
Рис 15- График полинома. Задание 6
Вычисления представлены на Рис 16
Рис 16- Вычисления в Задании 6
В результате использования функции datafit была подобрана аналитическая зависимость в виде полинома
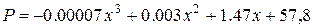
а сумма квадратов отклонений измеренных значений от расчетных составила 936,34 (Рис 16).
Заключение
В данной лабораторной работе были закреплены и усовершенствованы знания и практические навыки работы на персональном компьютере с использованием системы компьютерной математики SciLab.
Список литературы
|
|
|
1. Алексеев Е. Р. Scilab: Решение инженерных и математических задач / Е. Р. Алексеев. О. В. Чеснокова. Е. А. Рудченко. — М.: ALT Linux: БИНОМ. Лаборатория знаний. 2008. — 260с.
|
|
|
