 |
Принятие решений в условиях риска
|
|
|
|
Операции, выполняемые в условиях риска, называются вероятностными. Однозначность соответствия между вариантами действий (альтернативами) и достигаемыми при их реализации результатами в вероятностных операциях нарушается. Это означает (табл.5.1), что каждой альтернативе 
ставится в соответствие не один, а множество исходов 
с известными условными вероятностями появления 
.
Таблица 5.1
Оценка альтернатив в условиях риска
| 
| 
| 
| 
|
| 
| 
| 
|
|
|
| 
|
|
|
| … | … | … | … | … |
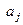
Эффективность систем в вероятностных операциях находится через математическое ожидание функции полезности на множестве исходов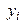 
(i = 1, …, n):
, j = 1, …, m,
где 
- функция полезности, выражаемая в стоимостной или иной формах (процент прибыли от инвестиций, качественное или количественное изменения ситуации на рынке и т.д.).
Критерием выбора альтернативы в условиях риска является максимальное значение математического ожидания функции полезности.
Оценка систем в условиях вероятностной операции – это оценка «в среднем», поэтому ей присущи все недостатки такого подхода, главный из которых заключается в том, что не исключен случай выбора неоптимальной системы для конкретной реализации операции. Однако если операция будет многократно повторяться, то оптимальная в среднем система приведет к наибольшему успеху [4].
Пример 4. Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиций может измениться в зависимости от условий на рынке ценных бумаг. Существует 10%-ная вероятность, что ситуация на рынке ухудшится, 50%-ная – что рынок останется умеренным и 40%-ная – рынок будет возрастать [3]. В табл.5.2 произведена оценка возможных альтернатив в условиях риска вложения инвестиций.
|
|
|
Таблица 5.2
Оценка альтернатив в условиях риска вложения инвестиций
|
Альтернативы (фонды),
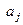
| Состояния природы (обстоятельства, которые от нас не зависят) – состояния рынка, исходы,
|
Условные вероятности исходов,
| Полезность (процент прибыли от инвестиций),
|
Математическое ожидание функции полезности,
|
| а 1 – простой | y 1 – ухудшающийся y 2 – умеренный y 3 – растущий | 0,1 0,5 0,4 | +5 +7 +8 | 0,1´5 + 0,5´7 + + 0,4´8 = 7,2 |
| а 2 – специальный | y 1 – ухудшающийся y 2 – умеренный y 3 – растущий | 0,1 0,5 0,4 | -10 +5 +30 | 0,1´(-10) + + 0,5´5 + + 0,4´30 = 13,5 |
| а 3 – глобальный | y 1 – ухудшающийся y 2 – умеренный y 3 – растущий | 0,1 0,5 0,4 | +2 +7 +20 | 0,1´2 + + 0,5´7 + + 0,4´20 = 11,7 |
Наибольшую оценку математического ожидания функции полезности получила альтернатива а 2, поэтому принимаем решение о выборе варианта вложения инвестиций в специальный фонд открытого типа.
Кроме оценки альтернатив на основе функции полезности могут использоваться и другие критерии оценки [4]:
§ максимум вероятности случайного события;
§ минимум дисперсии результата;
§ минимум среднего риска и др.
Рассмотрение этих критериев составляет один из разделов теории принятия решений.
3. Принятие решений в условиях неопределенности [4]
Отличие между принятием решений в условиях риска и в условиях неопределенности состоит в том, что в условиях неопределенности нет информации о вероятностях появления тех или иных состояний (исходов). Кроме того, специфические черты организационно-технических систем часто не позволяют свести операции, проводимые этими системами, к детерминированным или вероятностным. К таким чертам относятся:
|
|
|
1. Наличие в управляемой системе в качестве элементов (подсистем) целенаправленных индивидуумов и наличие в системе управления ЛПР, осуществляющих управление на основе субъективных моделей, что приводит к большому разнообразию поведения системы в целом.
2. Алгоритм управления часто строит сама система управления, преследуя помимо предъявляемых старшей системой целей собственные цели, не всегда совпадающие с внешними.
3. На этапе оценки ситуации в ряде случаев исходят не из фактической ситуации, а из той модели, которой пользуется ЛПР при управлении объектом.
4. В процессе принятия решения большую роль играют логические рассуждения ЛПР, не поддающиеся формализации классическими методами математики.
5. При выборе управляющего воздействия ЛПР может оперировать нечеткими понятиями, отношениями и высказываниями.
6. В большом классе задач управления организационно-техническими системами отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта управления, а также статистика, достаточная для построения соответствующих вероятностных распределений (законов распределения исходов операций) для конкретного принятого решения.
Таким образом, несводимость операций, проводимых сложными организационно-техническими системами к детерминированным или вероятностным, не позволяет использовать для их оценок детерминистские или вероятностные критерии.
В зависимости от характера неопределенности операции могут делиться на игровые и статистически неопределенные. В игровых операциях неопределенность вносит своими сознательными действиями противник (конкурент). Для исследования игровых операций используется теория игр. Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. Природа рассматривается как незаинтересованная, безразличная к операции сторона (она пассивна по отношению к ЛПР). Такие операции могут исследоваться с применением теории статистических решений.
В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:
§ среднего выигрыша;
|
|
|
§ Лапласа;
§ осторожного наблюдателя (Вальда);
§ максимакса;
§ пессимизма-оптимизма (Гурвица);
§ минимального риска (Сэвиджа).
Рассмотрим эти критерии на примере.
Пример 5. Необходимо оценить разрабатываемые программные продукты аj для борьбы с одним из четырех типов программных воздействий ki. Матрица эффективности представлена в табл.5.3, где 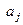- j -й программный продукт, j ={1,2,3}; ki - оценка эффективности применения i -го программного продукта, i ={1,2,3,4}, при j -м программном воздействии.
Критерий среднего выигрыша. Данный критерий предполагает задание вероятностей состояний обстановки pi. Эффективность вариантов оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям обстановки:
, j = 1, …, m.
Наиболее эффективному варианту будет соответствовать
, j = 1, …, m.
Таблица 5.2
Матрица эффективности программных продуктов
| 
| |||
| k 1 | k 2 | k 3 | k 4 | |
| a 1 | 0,1 | 0,5 | 0,1 | 0,2 |
| a 2 | 0,2 | 0,3 | 0,2 | 0,4 |
| a 3 | 0,1 | 0,4 | 0,4 | 0,3 |
Если задаться вероятностями применения противником программных воздействий: p 1 = 0,4; p 2 =0,2; p 3 = 0,1 и p 4 = 0,3, то получим следующие оценки вариантов программных продуктов:
;
;
.
Наиболее эффективное решение – программный продукт а 2.
Таким образом, для применения критерия среднего выигрыша необходимо, по существу, перевести задачу из класса задач в условиях неопределенности в задачу вероятностную, причем произвольным образом.
Критерий Лапласа. В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными. Тогда
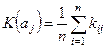, j = 1, …, m;
, j = 1, …, m.
Рассчитаем эффективность вариантов по данному критерию для нашего примера:
;
;
.
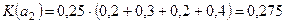Наиболее эффективное решение – программный продукт а 3. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.
Критерий осторожного наблюдателя (Вальда). Это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях. Критерий основывается на том, что, если состояние обстановки неизвестно, нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждого варианта.
|
|
|
В каждой строке матрицы эффективности находится минимальная из оценок вариантов по различным состояниям обстановки
, j = 1, …, m; i = 1, …, n.
Наиболее эффективному варианту соответствует максимальное значение эффективности
, j = 1, …, m; i = 1, …, n.
Применение критерия максимина к нашему примеру дает следующие оценки:
;
;
.
Наиболее эффективное решение – программный продукт а 2.
Максиминный критерий ориентирует на решение, не содержащее элементов риска: при любом из возможных состояний обстановки выбранная альтернатива покажет результат не хуже найденного максимина. Такая осторожность является в ряде случаев недостатком критерия.
Критерий максимакса. Этот критерий предписывает оценивать альтернативы по максимальному значению эффективности и выбирать в качестве наиболее эффективного вариант с наибольшим из максимумов:
, j = 1, …, m; i = 1, …, n.
, j = 1, …, m; i = 1, …, n.
Оценки альтернатив на основе максимаксного критерия в нашем примере принимают такие значения:
;
;
.
Наиболее эффективное решение – программный продукт а 1.
Критерий максимакса самый оптимистический критерий. Те, кто предпочитает им пользоваться, всегда надеются на лучшее состояние обстановки и, естественно, в большей степени рискуют.
Критерий пессимизма-оптимизма (Гурвица). Это критерий обобщенного максимина. Согласно данному критерию при оценке и выборе альтернативы неразумно проявлять как осторожность, так и азарт. Поэтому, учитывая самое высокое и самое низкое значения эффективности, следует занимать промежуточную позицию. Для этого вводится коэффициент оптимизма a (0 £ a £ 1), характеризующий отношение к риску ЛПР. Эффективность варианта находится как взвешенная с помощью коэффициента a сумма максимальной и минимальной оценок:
.
Наиболее эффективному варианту соответствует:
, 
.
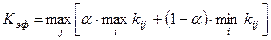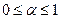Зададимся значением a = 0,6 и рассчитаем эффективность альтернатив для рассматриваемого примера:
;
;
.
Наиболее эффективное решение – программный продукт а 1.
При a = 0 критерий Гурвица сводится к критерию максимина, а при a = 1 – к критерию максимакса. Значение a может определяться методом экспертных оценок. На практике пользуются значениями коэффициента a = 0,3 … 0,7.
Критерий минимального риска (Сэвиджа). Этот критерий минимизирует потери эффективности при наихудших условиях. Для оценки вариантов матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок в столбце:
|
|
|
.
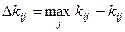После преобразования матрицы используется критерий минимакса:
;
.
Оценим эффективность альтернатив в рассматриваемом примере в соответствии с данным критерием. Матрице эффективности (см. табл.5.2) будет соответствовать матрица потерь (табл.5.3).
Таблица 5.3
Матрица потерь
|
|
| |||
| k 1 | k 2 | k 3 | k 4 | |
| a 1 | 0,1 | 0,3 | 0,2 | |
| a 2 | 0,2 | 0,2 | ||
| a 3 | 0,1 | 0,1 | 0,1 |
Тогда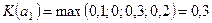 
;
;
.
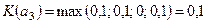Наиболее эффективное решение – альтернатива а 3.
О критерии Сэвиджа можно сказать, что он, как и критерий Вальда, относится к числу осторожных критериев, но по сравнению с критерием Вальда в нем придается несколько большее значение выигрышу, чем проигрышу.
Выбор какого-то одного критерия приводит к принятию решения, которое может быть отличным от решений, диктуемых другими критериями. Это наглядно подтверждают результаты оценки эффективности альтернатив в рассмотренном примере (табл.5.4).
Таблица 5.4
Сравнительные результаты оценки альтернатив
|
|
| по критериям
| ||||||||
| k 1 | k 2 | k 3 | k 4 | среднего выигрыша | Лапласа | Вальда | максимакса | Гурвица | Сэвиджа | |
| a 1 a 2 a 3 | 0,1 0,2 0,1 | 0,5 0,3 0,4 | 0,1 0,2 0,4 | 0,2 0,4 0,3 | 0,21 0,28 0,25 | 0,225 0,275 0,300 | 0,1 0,2 0,1 | 0,5 0,4 0,4 | 0,34 0,32 0,28 | 0,3 0,2 0,1 |
Таким образом, эффективность альтернатив в условиях неопределенности может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:
§ природа конкретной ситуации (в одних случаях допустим риск, в других – нужен гарантированный результат);
§ причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);
§ характер ЛПР (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).
В силу указанных факторов процесс выбора вида критерия для учета неопределенности носит достаточно сложный характер.
|
|
|
