 |
Основные теоретические сведения контрольной работы 3
|
|
|
|
МАТЕМАТИКА
Методические указания к выполнению контрольной работы 3
для студентов направления «Химическая технология»
заочной формы обучения
Балаково 2015
Введение
Изучение математики для инженерно-технических специальностей и направлений ставит следующие цели:
- ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических инженерно-технических задач;
- привить навыки самостоятельного изучения учебной литературы по математике и ее спецглавам;
- развить логическое мышление и выработать навыки математического исследования прикладных вопросов, а также научить составлять математические модели инженерных задач.
Методические указания к выполнению, оформлению и сдаче контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для доработки.
1. Студент должен выполнить контрольную работу по варианту, номер которого совпадает с последней цифрой номера зачетной книжки или студенческого билета.
2. Каждая контрольная работа выполняется в отдельной тетради в клетку чернилами любого цвета, кроме красного.
3. На титульном листе разборчиво пишутся фамилия и инициалы студента, учебный номер (шифр), название дисциплины, номер контрольной работы, название учебного заведения. В конце работы следует поставить дату ее выполнения и подпись студента.
4. В работу включаются все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие лишь часть задания, а также задачи не своего варианта, не засчитываются и возвращаются студенту.
|
|
|
5. Решения задач надо располагать в порядке возрастания номеров, указанных в заданиях, сохраняя номера задач.
6. Перед решением каждой задачи следует полностью записать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными соответствующего номера.
7. Решения задач излагать подробно и записывать аккуратно, объясняя все действия и делая необходимые чертежи.
8. После получения проверенной работы (как не зачтенной, так и зачтенной) студент должен исправить в ней все отмеченные ошибки и недочеты.
9. Рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений.
Содержание контрольной работы 3 и примеры выполнения задач
Темы контрольной работы 3
1. Кратные интегралы.
2. Криволинейные и поверхностные интегралы.
3. Элементы теории поля.
4. Ряды.
Основные теоретические сведения контрольной работы 3
Л и т е р а т у р а: [1], гл. XI, XII, XIII, XIV, XV, ХVI; [2], гл. I, III, IV, V; [3], гл. XII, XIII, XIV; [4], VII, VIII, IX.
1. Вычисление двойного интеграла от функции f(x,y), определенной в плоской области D, сводится к вычислению двукратного интеграла вида
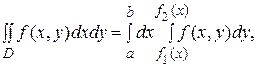(1)
если область D определяется условиями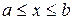 
, 
(рис.1), или к вычислению двукратного интеграла вида
, (2)
если область D определяется условиями 
, 
(рис. 2).
Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводятся новые переменные под знаком двойного интеграла. Перейдем в данном двойном интеграле 
к полярным координатам r и 
: 
, 
.
Формула перехода к полярным координатам в двойном интеграле имеет вид: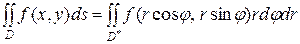 
, (3)
где 
- область в полярной системе координат, соответствующая области D в декартовой системе координат.
С помощью двойного интеграла можно найти площадь плоской фигуры D по формуле: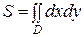 
. (4)
|
|
|
2. Вычисление тройного интеграла от функции f(x,y,z), определенной в области V, сводится к вычислению интеграла вида
, (5)
где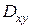 
- проекция области V на плоскость Оху;
, 
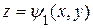- уравнения поверхностей, ограничивающих область V соответственно снизу и сверху.
Наряду с прямоугольными координатами 
точки, в пространстве могут быть определены ее цилиндрические координаты 
(рис.3) и сферические координаты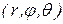 
(рис.4):
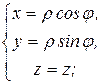
Тройной интеграл записывается в виде:
(6)
С помощью тройных интегралов можно вычислить объем V тела и массу m тела по формулам:
, 
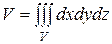, (7)
где 
- объемная плотность.
3. Если пространственная кривая L (АВ) задана уравнениями в параметрической форме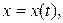 
, 
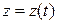, причем точке А соответствует 
, точке В - 
, то криволинейный интеграл I рода определяется по формуле:
. (8)
4. Вычисление криволинейного интеграла II рода по кривой L(AB) сводится к вычислению определенного интеграла по формуле:
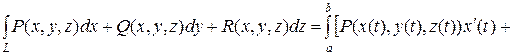
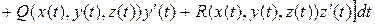, (9)
если кривая L задана параметрически х=х(t), y=y(t), z=z(t), t=a соответствует начальной точке А, t=b - конечной точке В кривой L.
5. Вычисление поверхностного интеграла I рода по поверхности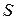 
сводится к вычислению двойного интеграла по плоской области:
а) если поверхность S задана уравнением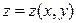 
, 
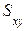- однозначная проекция поверхности S на плоскость Оху, то поверхностный интеграл 1-го рода вычисляется следующим образом:
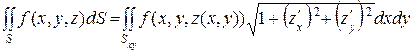, (10)
б) если поверхность S задана уравнением 
, 
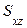- однозначная проекция поверхности S на плоскость Охz, то поверхностный интеграл 1-го рода вычисляется следующим образом:
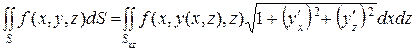, (11)
в) если поверхность S задана уравнением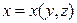 
, 
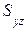- однозначная проекция поверхности S на плоскость Оyz, то поверхностный интеграл 1-го рода вычисляется следующим образом:
. (12)
6. Вычисление интеграла II рода по выбранной стороне поверхности S сводится к вычислению двойных интегралов по плоским областям:
(13)
где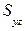 
, 
, 
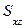- проекции поверхности S на плоскости Оyz, Oxz, Oxy соответственно; 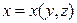, , 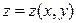- уравнения плоскости S, разрешенные относительно разных переменных. Знаки перед интегралами берутся в зависимости от ориентации поверхности S: если углы 
, 
, 
между осями Ох, Оу, Оz и нормалью 
к выбранной стороне поверхности острые, то перед соответствующими интегралами ставятся плюсы, в противном случае – минусы.
|
|
|
5. Векторным полем называется область V, в каждой точке которой определена векторная функция:
. (14)
Векторное поле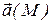 
характеризуется скалярной величиной – дивергенцией 
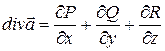(15)
и векторной величиной – ротором
. (16)
Потоком векторного поля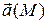 
через выбранную сторону поверхности S называется поверхностный интеграл
, (17)
где 
- скалярное произведение векторов 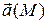и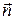 
,
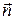- единичный вектор нормали к выбранной стороне поверхности S.
Если поверхность 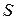задана уравнением 
, то координаты единичного вектора нормали 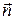определяются по формуле:
. (18)
Циркуляцией векторного поля
называется криволинейный интеграл II рода по кривой L:
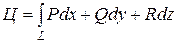(19)
6. Числовым рядом называется выражение вида
, (20)
где 
- члены ряда;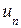 
- общий член ряда.
Ряд (20) называется сходящимся, если существует предел его частичных сумм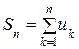 
. Число 
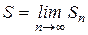называется суммой ряда. Если же предел частичных сумм не существует, то ряд (20) называется расходящимся.
Необходимый признак сходимости: Если ряд (20) сходится, то 
.
Достаточные признаки сходимости знакоположительных рядов (
):
а) Признак сравнения в предельной форме: Если
(21)
то ряды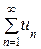 
и 
одновременно сходятся или расходятся.
В качестве эталонных рядов для сравнения обычно служат:
- обобщенный гармонический ряд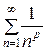 
, сходящийся при 
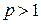и расходящийся при 
;
- ряд геометрической прогрессии 
, сходящийся при 
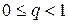и расходящийся при 
.
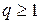б) Признак Даламбера: Если существует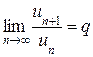 
, (22)
то ряд 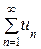сходится при 
, расходится при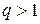 
. Если же 
, то вопрос о сходимости ряда этим признаком не решается.
Знакочередующимся рядом называется ряд вида:
. (23)
Признак Лейбница сходимости знакочередующегося ряда: Если ряд 
удовлетворяет условиям: 1)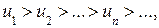 
2) 
,
то ряд сходится.
7. Степенным рядом по степеням переменной х называется ряд вида
, (24)
где аn – коэффициенты ряда.
Число R называется радиусом сходимости степенного ряда (24), если ряд сходится при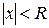 
и расходится при 
.
При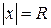 
ряд может как сходиться, так и расходиться. Интервал 
называется интервалом сходимости степенного ряда (24).
Радиус сходимости R может быть найден по формуле:
|
|
|
(25)
Разложения функций в ряд Маклорена:
,
,
,
.
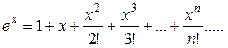
8. Рядом Фурье функции f(x) на отрезке длины 2l называется ряд вида
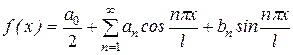, (26)
где
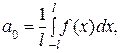
. (27)
Функция, заданная на полупериоде 
, может быть представлена различными рядами Фурье. При четном продолжении данной функции на второй полупериод 
получается ряд по косинусам:
, (28)
, 
,
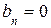а при нечетном продолжении – ряд по синусам:
, (29)
, 
.
|
|
|
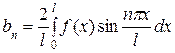