Примеры выполнения задач контрольной работы №3

Пример 1. Вычислить площадь плоской фигуры, ограниченной линиями y=x², y=2-x.

Р е ш е н и е. Плоская фигура D ограничена:

слева и справа – прямыми х=-2 и х=1,

снизу – параболой у=х²,

сверху – прямой y =2- x (рис.5).

Находим площадь:

.

Пример 2. Вычислить тройной интеграл , если область V ограничена поверхностями : z =1, :

Р е ш е н и е. Область V, ограничена плоскостью (рис.6) и параболоидом вращения .

Проекцией D_xy области V на плоскость Oхy является круг .

Переходим к цилиндрическим координатам с пределами интегрирования

, , ,

где - уравнение параболоида в цилиндрических координатах:

 

.

Пример 3. Вычислить поток векторного поля через замкнутую поверхность S, образованную плоскостью z =1 и параболоидом (рис. 6).

Р е ш е н и е. Поверхность S состоит из двух поверхностей: – части плоскости z =1 и – части параболоида . В силу этого поток через S равен сумме потоков вектора :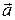

где и - внешние нормали к плоскости и к параболоиду.

Для поверхности z =1 в силу формулы (18) получим , и, значит,

так как на поверхности имеем z =1.

Найдем единичный вектор внешней нормали к поверхности :

.

Здесь в выражении для нормали выбран знак минус, так как угол γ между осью Oz и нормалью - острый.

Вычислим поток через ;

Таким образом, поток через поверхность 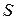σ равен

Пример 4. Вычислить поверхностный интеграл ,

где - часть параболоида , отсекаемая плоскостью z=1 (рис.6).

Р е ш е н и е. Так как поверхность однозначно проектируется на плоскость Oхy в область D_xy, то получаем:

Рис. 3

Область D_xy есть круг . Поэтому в последнем интеграле переходим к полярным координатам (при этом , ):

.

Пример 5. Найти дивергенцию и ротор векторного поля .

Р е ш е н и е. По формуле (15) получаем

.

Ротор данного векторного поля находим по формуле (16):

Пример 6. Вычислить циркуляцию векторного поля

по контуру Г, образованному пересечением поверхностей

, .

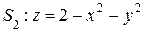Р е ш е н и е. Пересечением указанных поверхностей является окружность , (рис. 6). Направление обхода контура Г выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические уравнения контура Г:

причем параметр t изменяется от 0 до 2 . По формуле (19) получаем:

.

Пример 7. Исследовать на сходимость ряд .

Р е ш е н и е. Проверяем сходимость ряда по признаку Даламбера. Так как общий член ряда , то заменяя в выражении n -го члена n на n+1, находим . Затем ищем предел отношения последующего члена к предыдущему при :

,

Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда. Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем обобщенный гармонический ряд

и в силу формулы (21) получим

.

Следовательно, исследуемый ряд является сходящимся, так как эталонный ряд сходится (р =2>1).

Пример 8. Найти радиус и интервал сходимости ряда .

Исследовать сходимость ряда на концах интервала сходимости.

Р е ш е н и е. Радиус сходимости находим по формуле:

.

Интервал сходимости данного ряда определяется неравенством

или .

Исследуем концы интервала сходимости.

При х=-2 получаем числовой знакочередующийся ряд:

.

Этот ряд расходится, так как не выполняется необходимый признак сходимости:

.

При x=4 получаем знакоположительный ряд

,

расходящийся, так как .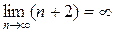

Пример 9. Вычислить с точностью до .

Р е ш е н и е. Используем разложение 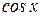в ряд Маклорена:

.

Заменяя х на , имеем

Подставляя это разложение в интеграл и интегрируя в указанных пределах, получаем

Четвертый член этого знакочередующегося сходящегося ряда меньше 0,001. Поэтому для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться первыми тремя членами ряда:

Пример 10. Разложить функцию в ряд Фуье по косинусам

Р е ш е н и е. Данная функция определена на полупериоде [0,2], т.е. l =2.

Для разложения такой функции в ряд Фурье по косинусам ее следует продолжить на второй полупериод [-2,0) четным образом. Для четной функции коэффициенты , а коэффициенты вычисляются по формулам:

,

Так как ,

Искомое разложение функции в ряд Фурье по косинусам имеет вид

.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: