 |
Классификация элементов конструкций
|
|
|
|
Стержень (брус) – тело, длина которого L превышает его поперечные размеры b и h. Ось стержня – линия, соединяющая центры тяжести последовательно расположенных сечений. Сечение – это плоскость перпендикулярная оси стрежня.
Пластина – тело плоской формы, у которого длина a и ширина b больше по сравнению с толщиной h.
Оболочка – тело, ограниченное двумя близко расположенными криволинейными поверхностями. Толщина оболочки мала по сравнению с другими габаритными размерами, радиусами кривизны ее поверхности.
Массивное тело (массив) – тело, у которого все размеры одного порядка.
Напряжение
Нормальные напряжения, касательные напряжения. Полное напряжение.
Определение зависимости между внешними силами, с одной стороны, и напряжением и деформацией, с другой, - основная задача сопротивлению материалов.
Растяжение и сжатие
Растяжение или сжатие часто встречаются в элементах машин или сооружений (растяжение троса крана при подъеме груза; шатуна двигателя, штока цилиндров в подъёмно-транспортных машинах).
Растяжение или сжатие – это случай нагружения стрежня, который характеризуется его удлинением или укорочением. Растяжение или сжатие вызывается силами, действующими вдоль оси стрежня.
При растяжении стержень удлиняется, а его поперечные размеры уменьшаются. Изменение начальной длины стрежня называют абсолютным удлинением при растяжении или абсолютным укорочением при сжатии. Отношение абсолютного удлинения (укорочение) к начальной длине стрежня называется относительным удлинением.
В этом случае:
· ось стержня остается прямой линией,
· поперечные сечения стержня уменьшаются вдоль его оси параллельно самим себе (потому что поперечное сечение - это плоскость перпендикулярная оси стрежня, а ось - прямая линия);
|
|
|
· поперечные сечения остаются плоскими.
Все волокна стрежня удлиняются на одну и ту же величину и их относительные удлинения одинаковые.
Разность соответствующих поперечных размеров после деформации и до нее называется абсолютной поперечной деформацией.
Отношение абсолютной поперечной деформации к соответствующему начальному размеру называется относительной поперечной деформацией.
Между поперечной и продольной деформациями существует соотношение. Коэффициент Пуассона − безразмерная величина, находящаяся в пределах 0...0,5 (для стали 0,3).
В поперечных сечениях возникают нормальные напряжени я. Зависимость напряжений от деформаций устанавливает закон Гука.
В сечении стержня возникает один внутренний силовой фактор – продольная сила N. Продольная сила N является равнодействующей нормальных напряжений, которая численно равна алгебраической сумме всех внешних сил, действующих на одну из частей рассеченного стрежня и направленных вдоль его оси.
При решении задач сопротивления материалов широко применяют уравнения равновесия различных систем сил, полученные в статике абсолютно твердого тела. Вместе с тем не все приемы и методы статики могут быть использованы в сопротивлении материалов. Замена одной системы сил другой, статически эквивалентной, в частности перенос силы по линии ее действия и замена ряда сил их равнодействующей, резко изменяет характер деформации детали и поэтому недопустима. Поясним это положение некоторыми примерами.
Рисунок 2.1.3
На рис, 2.1.3,а изображена балка, нагруженная парой сил на левой опоре. Штриховой линией показан характер ее деформации. При переносе этой пары сил в положение, показанное на рис. 2.1,3,б, характер деформации резко изменяется. При втором положении нагрузки допускаемое по условию прочности значение момента пары вдвое больше, чем в первом. Реакции опор балки в том и другом случаях, конечно,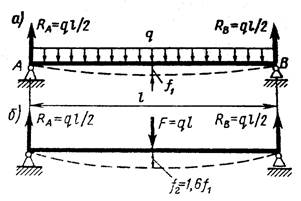 
одинаковы.
|
|
|
Рисунок 2.1.4
На рис. 2.1.4, а, 6 показаны две одинаковые балки, первая нагружена равномерно распределенной нагрузкой интенсивностью q, а вторая — силой F = q1 (т. е. силой, равной равнодействующей этой нагрузки). Опорные реакции рассматриваемых балок одинаковы, но наибольший прогиб второй балки в 1,6 раза большие, чем первой, а допускаемая по условию ее прочности нагрузка вдвое меньше-
Из рассмотренных примеров следует, что при определении опорных реакций в статически определимых системах статически эквивалентные преобразования нагрузки допустимы, но при вычислении перемещений и расчетах на прочность замена некоторой системы сил другой, статически эквивалентной заданной, приводит к весьма серьезным ошибкам.
|
|
|
