 |
Математическая модель и метод численного моделирования
|
|
|
|
Формирование функциональных поверхностей с микро- и нанопараметрами при анодном растворении металлов и сплавов с использованием диэлектрических масок
Постановка задачи
Анодное растворение материала заготовки, часть поверхности которой закрыта диэлектрической маской (рис. 1), происходит как в вертикальном, так и в горизонтальном направлениях. Поэтому горизонтальный размер B полученного элемента поверхности всегда больше размера пробельного участка маски b. Часто маска имеет пробельные участки различной формы и размеров. Так как плотность тока, а, следовательно, скорость анодного растворения зависит от доли активной поверхности, то в результате обработки получаются структурные элементы поверхности разной глубины. Например, в зоне I, где доля активной поверхности меньше, чем в зоне II, будут сформированы элементы большой глубины (рис.1). Кроме того, из-за экранирующего эффекта соседних пробельных участков, глубина элементов рельефа будут различной в пределах каждой из зон. Например, в зоне I глубина элемента (2), соответствующего большему пробельному участку, будет больше, чем глубина элемента (1), соответствующего меньшему пробельному участку. Даже глубина элементов, имеющих одинаковые размеры, но различную форму (рис. 1, зона III) будет различной: из-за большего влияния краевого эффекта осесимметричный элемент (4) будет иметь большую глубину, чем, прямолинейный элемент (3).
Для формирования нано- и микроструктурированных поверхностей часто используются маски с цилиндрическими порами (рис. 2) или маски из коллоидного кристалла, образованного из монодисперсных сферических частиц (рис. 3).
Рисунок 1 - Схема анодного растворения через диэлектрическую маску:
|
|
|
I – зона с малой долей активной поверхности; II – зона с большой долей активной поверхности; III – зона с пробельными участками разной геометрической формы;(1) – (4) – элементы поверхности, соответствующие различным элементам маски; S – межэлектродный зазор; h – толщина маски; b – ширина пробельного участка; H – глубина элемента, сформированного на обработанной поверхности; t – подтравливание.
Рисунок 2 - Схема наноструктурирования поверхности при анодном растворении через маску с цилиндрическими порами: (а) маска с цилиндрическими порами на поверхности металлической подложки; (б) наноструктурирование поверхности металла анодным растворением через маску; (в) наноструктурированная поверхность после удаления маски.
Рисунок 3 - Схема формирования наноструктурированной поверхности анодным растворением через маску из коллоидного кристалла:
(а) металлическая подложка с маской до начала обработки; (б) металлическая подложка с маской в процессе обработки; (в), (г) наноструктурированная поверхность металла после удаления маски; (в) частично наноструктурированная поверхность; (г) полностью наноструктурированная поверхность.
Для прогнозирования формы и размеров обработанной поверхности или определения формы и размеров пробельных участков маски, обеспечивающих получение требуемой геометрии обработанной поверхности, целесообразно использовать методы компьютерного моделирования.
Математическая модель и метод численного моделирования
В качестве математической модели будем использовать уравнение Лапласа для потенциала электрического поля в растворе электролита (1) и уравнение эволюции обрабатываемой поверхности (2):
(1)
(2)
где 
, 
- безразмерные координаты; 
- безразмерная функция, описывающая обрабатываемую поверхность; 
- безразмерный потенциал; 
- безразмерное время; N – ось, направленная по нормали к обрабатываемой поверхности.
|
|
|
При переходе к безразмерным переменным в качестве единицы длины был принят характерный размер для маски, рассматриваемого типа (расстояние между соседними пробельными участками, диаметр поры или диаметр сферических частиц), а в качестве единицы потенциала – приложенное напряжение.
В качестве граничных условий будем использовать следующие соотношения:
(3)
где Wa – безразмерное число Вагнера, характеризующее поляризацию электрода; А, В, М – нижние индексы, относящиеся к поверхности анода, верхней границе расчетной области и боковой поверхности пробельного участка (поры), соответственно.
В качестве начального условия примем:
, (4)
что соответствует исходной плоской поверхности металлической подложки.
При моделировании будем использовать квазистационарное приближение, в соответствии с которым при расчете распределения потенциала не учитывается движение поверхности подложки вследствие ее анодного растворения, а при расчете эволюции обрабатываемой поверхности используется распределение потенциала, полученное на предыдущем шаге. Таким образом, на каждом шаге по времени:
- рассчитывается вторичное распределение плотности тока в единичной ячейке в результате решения уравнения Лапласа;
- определяется новое положение анодной поверхности в результате решения уравнения (2).
Для численного решения уравнения Лапласа использовался метод граничных элементов, важным достоинством которого является простота перестроения сетки при изменении геометрии расчетной области в результате анодного растворения подложки. При этом уравнение Лапласа сводилось к граничному интегральному уравнению:
(5)
Численное решение уравнения (5) осуществлялось обычным методом граничных элементов (объем вычислений от N 2 до N 3 в зависимости от метода решения системы линейных алгебраических уравнений)
(6)
где 
.
Обычный метод граничных элементов не позволяет использовать достаточно мелкие сетки, обеспечивающие достаточную точность расчета распределения потенциала, поэтому также был использован быстрый мультипольный метод граничных элементов (объем вычислений от N дo N 2 в зависимости от метода решения системы линейных алгебраических уравнений). В случае использования быстрого мультипольного метода граничных элементов коэффициенты системы разностных уравнений определялись с использованием следующих соотношений:
|
|
|
(7)
где 
; 
- базовая точка разложения; 
- координаты точки 
в сферической системе координат; 
- ассоциированная функция Лежандра; 
.
Для численного решения уравнения эволюции обрабатываемой поверхности был использован метод “Level Set”. Разностная форма уравнения (2) на сетке из равносторонних треугольных элементов может быть записана в следующем виде:
(8)
где n – номер шага по времени; i – номер расчетной точки; 
- шаг по времени.
Значения производных по пространственным координатам в соотношении (8) рассчитывались с использованием следующих соотношений:
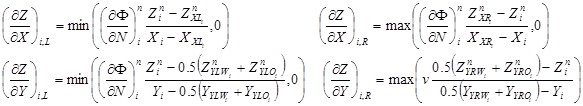(9)
Соотношения (9) являются обобщением известных соотношений метода “Level Set” для конечно-разностной сетки. Как видно из рис. 4 в случае сетки из равносторонних треугольных элементов для аппроксимации производных по оси X можно непосредственно использовать соотношения для конечно-разностной сетки, в то время как, для аппроксимации производных по оси Y требуется использовать среднее значение для двух соседних узлов (YWR и YRO или YLW и YLO).
После каждого шага по времени производилась перестроение сетки на боковых поверхностях расчетной области.
Рисунок 4 - Схема аппроксимации производных по пространственным координатам на сетке из равносторонних треугольных элементов по методу “Level Set”
|
|
|
