 |
Формирование функциональных поверхностей с микро- и нанопараметрами при катодном электроосаждении металлов и сплавов в поры матрицы с переменной пористостью
|
|
|
|
Формирование функциональных поверхностей с микро- и нанопараметрами при катодном электроосаждении металлов и сплавов в матрицу с цилиндрическими порами
Постановка задачи
На рис. 1 представлена схема электроосаждения металла в цилиндрические регулярно расположенные поры матрицы.
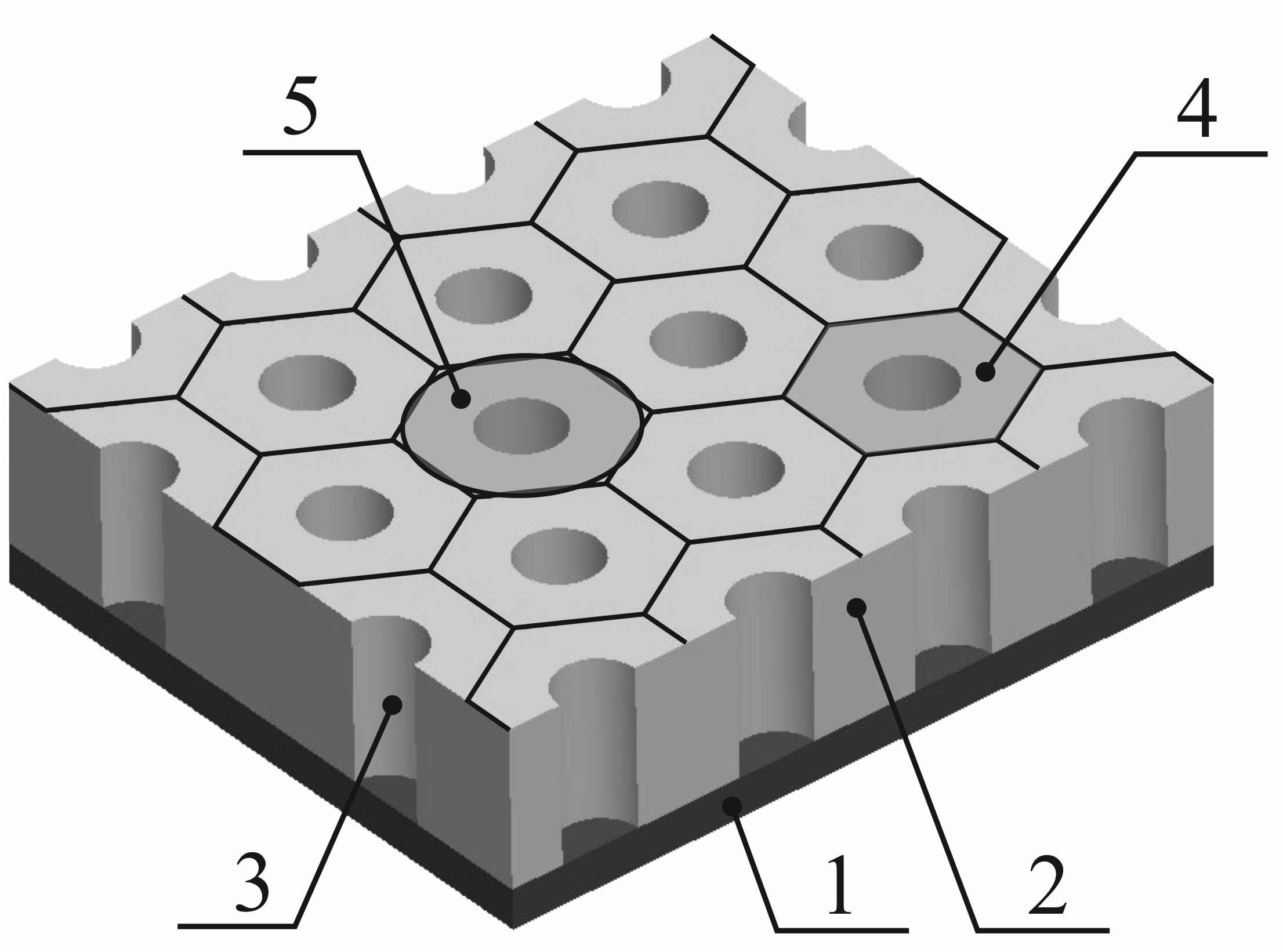
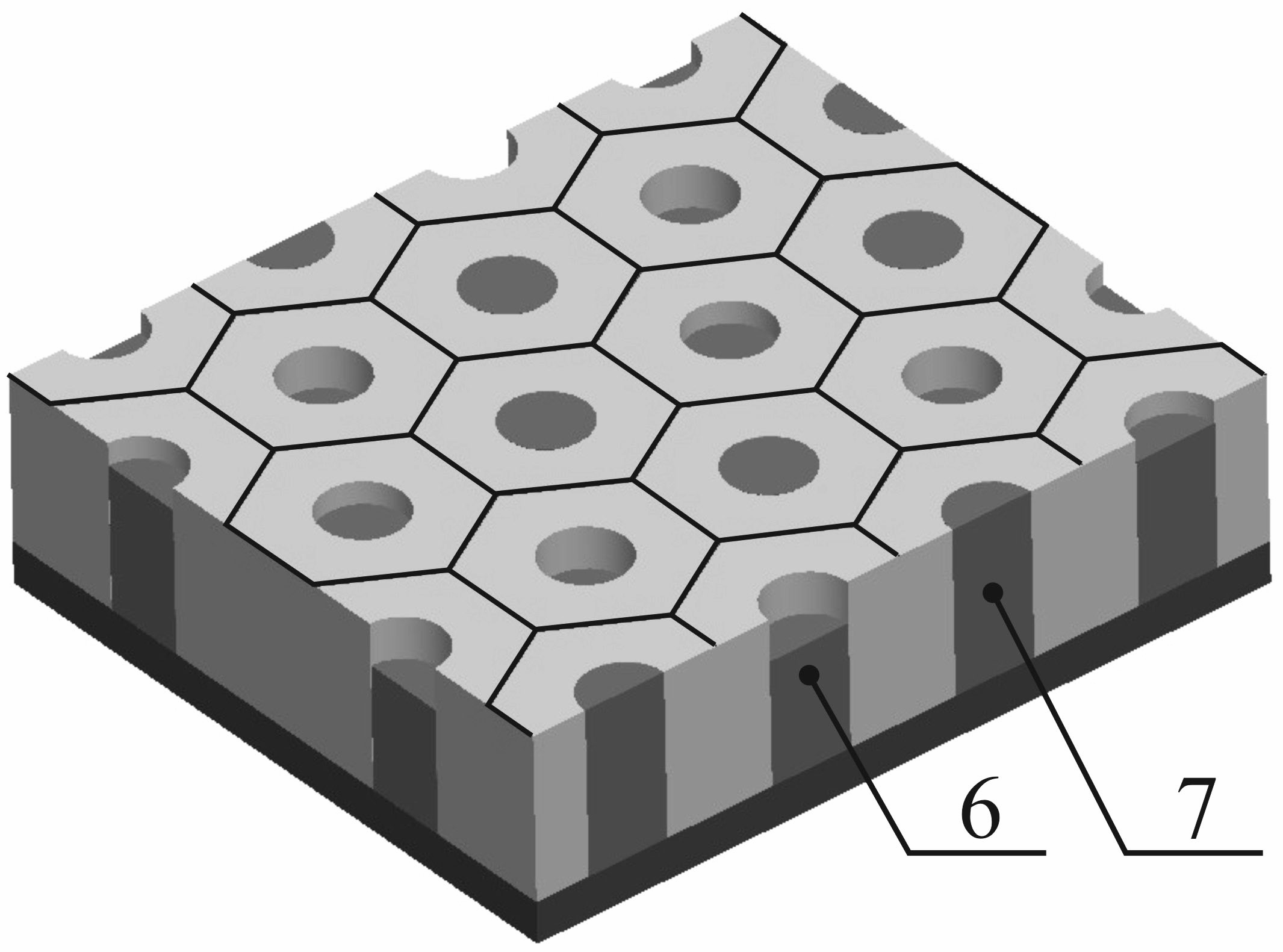
Рисунок 1 - Схема электроосаждения металлы в цилиндрические поры:
1 – токопроводящий слой, выполняющий функция токоподвода к катоду;
2 – нанопористая матрица; 3 – пора матрицы; 4 – поверхность матрицы, соответствующая поре; 5 – осесимметричная аппроксимация поверхности матрицы, соответствующей поре; 6 – частично заполненная пора;
7 – полностью заполненная пора
Можно выделить три главных стадии заполнения пор металлом:
(1) Стадия нестационарной диффузии. После приложения потенциала ток быстро увеличивается, а затем уменьшается с течением времени из-за увеличения толщины диффузионного слоя от нуля до некоторого значения, которое определяется условиями проведения процесса. На этой стадии выполняется уравнения Коттрелла.
(2) Основная стадия заполнения пор металлом. На этой стадии ток увеличивается с течением времени из-за уменьшения длины незаполненной металлом части пор. Длительность этой стадии (tfill) существенно больше, чем длительность первой стадии.
(3) После заполнения пор, металлические нанопроволочки выходят за поверхность темплета и постепенно вся поверхность АОА покрывается сплошным слоем металла. На этой стадии с течением времени увеличивается эффективная поверхность катода, что приводит к увеличению тока, до тех пор пока вся поверхность не будет покрыта металлом. В дальнейшем ток с течением времени не изменяется.
|
|
|
Величина тока и время заполнения пор tfill зависят от потенциала электрода зависят от условий проведения процесса. Для получения количественных зависимостей, характеризующих рассматриваемый процесс будем использовать методы математического моделирования.
Математическая модель
При построении математической модели примем следующие допущения:
(1) Допустимость использования квазистационарной одномерной аппроксимации. Эта аппроксимация базируется, во-первых, на большом аспектном отношении пор: длина пор много (на два-три порядка) больше, чем радиус пор. Во-вторых, время формирования диффузионного слоя на несколько порядков меньше, чем время заполнения пор металлом.
(2) Концентрация катионов металла в устье поры определяется осредненным потоком катионов во внешнем диффузионном слое, а не их потоком внутри индивидуальной поры. Это допущение базируется на том факте, что расстояние между соседними порами сравнимо с радиусом пор. Учет внешнего диффузионного слоя позволяет учитывать взаимодействие между процессами осаждения металла в разных порах. При этом расстояние между соседними порами считается много меньше, чем толщина внешнего диффузионного слоя, поэтому может быть использован общий внешний диффузионный слой.
Расчетная схема представлена на рис. 2.
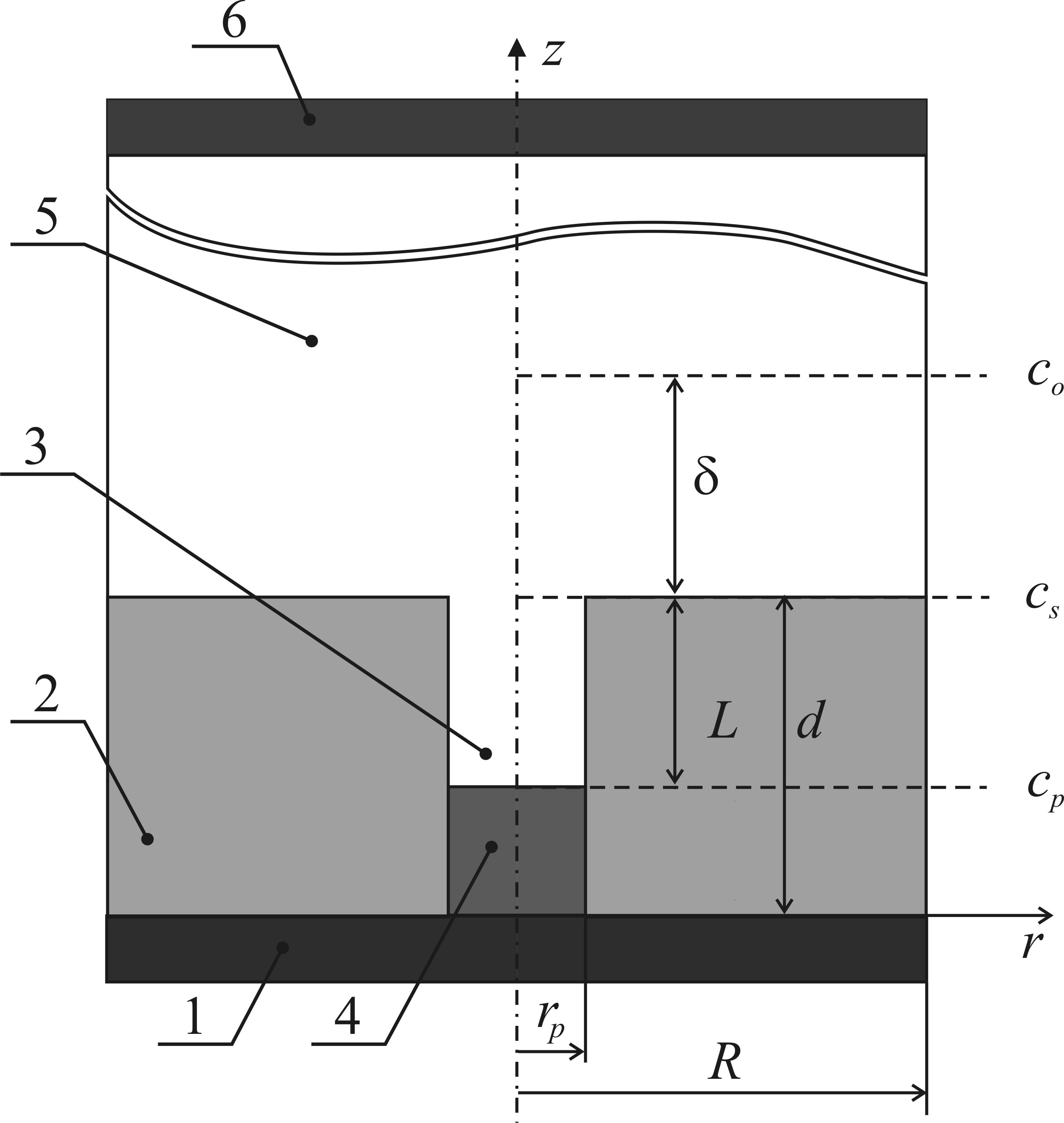
Рисунок 2 - Схема для расчета массопереноса при электроосаждении металла в пору: 1 – проводящий слой (токоподвод); 2 – матрица; 3 – пора; 4 – часть поры, заполненная металлом; 5 – пространство между матрицей и вспомогательным электродом, заполненное раствором электролита;
6 – вспомогательный электрод (анод)
В случаепор одинаковой длины будут выполняться следующие соотношения:
, (1)
где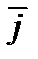 
- средняя плотность тока; D – коэффициент диффузии электроактивных катионов; n – валентность электроактивных катионов; F – число Фарадея; 
- отношение коэффициента диффузии катионов в “свободном электролите” к коэффициенту их диффузии в поре; Γ – отношение между потоком электроактивных ионов к электроду с частично изолированной поверхностью к потоку этих катионов к неизолированному электроду (поверхность частично изолированного электрода состоит из активных зон – пор, и неактивных зон – поверхность непроводящего Al2O3); c0, cs – концентрация катионов металла в объеме раствора электролита и в устье поры, соответственно.
|
|
|
Диффузионный ток в одной поре jp, определяется так:
, (2)
Из условия сохранения электроактивных катионов имеем следующее соотношение между средней плотностью тока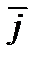 
, плотностью тока в поре и пористостью:
. (3)
Плотность тока jp зависит от перенапряжения электрохимической реакции 
. Для учета этой зависимости будем использовать уравнение Тафеля:
, (4)
где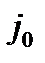 
- плотность тока обмена; α – коэффициент переноса; R – универсальная газовая постоянная; T - температура.
Плотность тока связана со скоростью изменения толщины металлического осадка уравнением Фарадея:
, (5)
где М – молярная масса металла; 
- плотность металла.
С учетом соотношений (1-5), мы получим следующее дифференциальное уравнение, описывающее заполнение пор матрицы металлом:
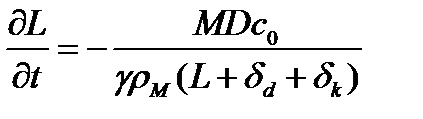. (6)
где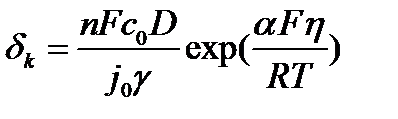 
- параметр, связанный с Тафелевской кинетикой электроосаждения металла, который может быть формально представлен в виде дополнительной длины поры (дополнительной толщины диффузионного слоя); 
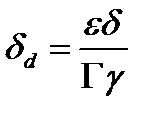- параметр, который может рассматриваться как эффективная толщина внешнего диффузионного слоя.
Начальные условия для уравнения (6) определяются толщиной пористой матрицы 
:
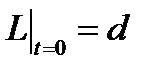. (7)
Уравнение (6) легко интегрируется, что с учетом начального условия (7) приводит к следующему соотношению, характеризующему зависимость L от времени:
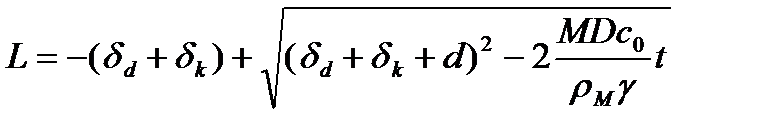. (8)
Средняя плотность тока по поверхности образца может быть рассчитана по следующему соотношению:
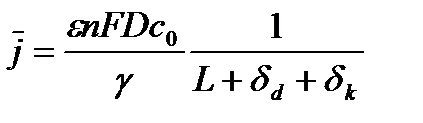. (9)
Концентрация катионов в устье поры может быть определена с использованием соотношений (2), (3), (5) и (8):
. (10)
Уравнения подобные соотношениям (8)-(10) и их следствия рассматривались в работе [50].
Рассмотрим теперь случай, когда поры имеют различную начальную длину. В этом случае для образца с площадью поверхности S будут справедливы следующие соотношения:
|
|
|
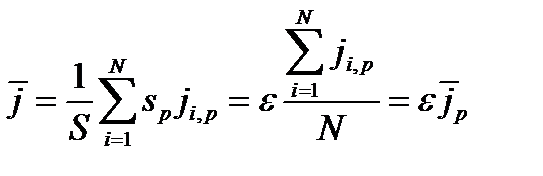, (11)
где N – общее число пор;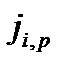 
- плотность тока в i -ой поре; 
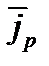- средняя плотность тока в порах; S – общая площадь образца; 
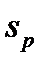- площадь поперечного сечения одной поры.
Для средней концентрации катионов в устье пор будем иметь следующее соотношение:
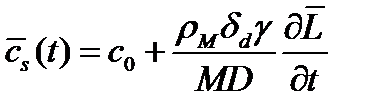, (12)
где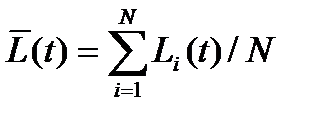 
- средняя длина пор.
Уравнение (6) в случае пор разной длины примет следующий вид:
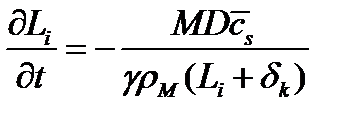. (13)
с начальными условиями для каждой поры:
. (14)
Начальная длина пор 
различна и имеет некоторое среднее значение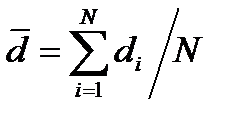 
.
Решение системы уравнений (13) с начальными условиями (14) имеет вид:
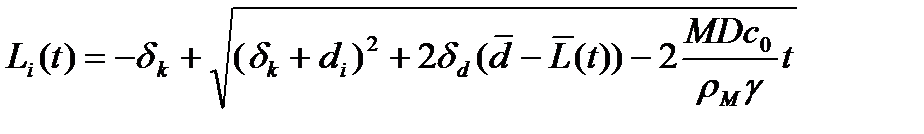. (15)
Средняя длина незаполненной части поры 
может быть определена с использованием следующего соотношения:
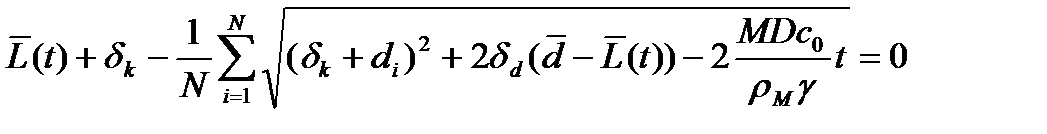. (16)
В общем случае решение уравнения (16) возможно лишь с использованием численных методов. Однако в случае нормального начального распределения длин пор возможно получение аналитического решения.
Рассмотрим случай нормального распределения пор по длине, кроме того будем считать, что пор достаточно много и суммирование можно заменить на интегрирование. Пусть 
- относительное отклонение длины поры от среднего значения. Тогда соотношение (15) можно записать в следующем виде:
. (17)
Уравнение (16) в непрерывном случае можно записать в виде:
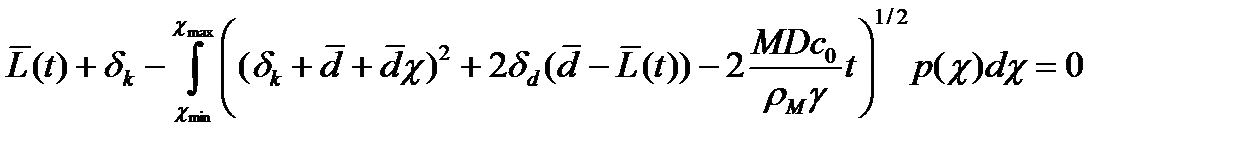. (18)
где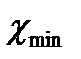 
и 
минимальные и максимальные отклонения от средней длины, 
плотность вероятности безразмерного отклонения длины поры от средней длины.
Зададимся теперь распределение - пусть оно будет нормальным с дисперсией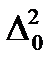 
, а 
и 
примем меняющимся в бесконечных пределах.
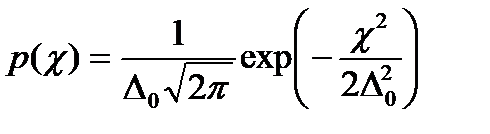. (19)
а уравнение (18) можно переписать в виде:
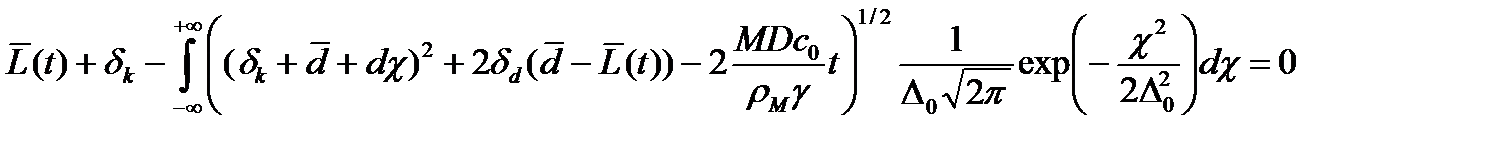. (20)
Применяя метод Лапласа (учитывая, что 
малый параметр) находим в главном значении
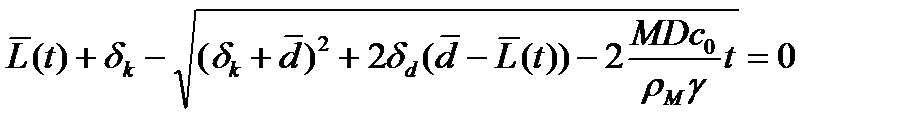. (21)
И таким образом в главном порядке по малости дисперсии будет выполняться следующее соотношение:
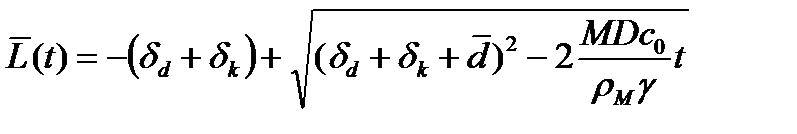. (22)
Так же полезно получить выражение для зависимости дисперсии от времени
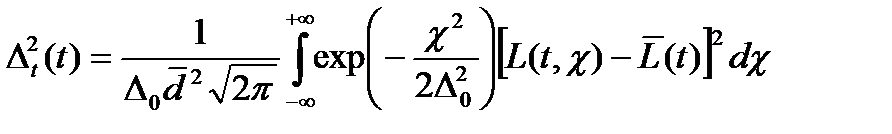. (23)
Пользуясь тем же приемом из метода Лапласа, с учетом того, что разлагая (17) в ряд Тейлора около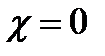 
мы получаем для малых 
. (24)
Окончательно получаем в главном порядке по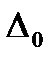 
из (23) с учетом того, что нечетные степени обнуляются после интегрирования:
|
|
|
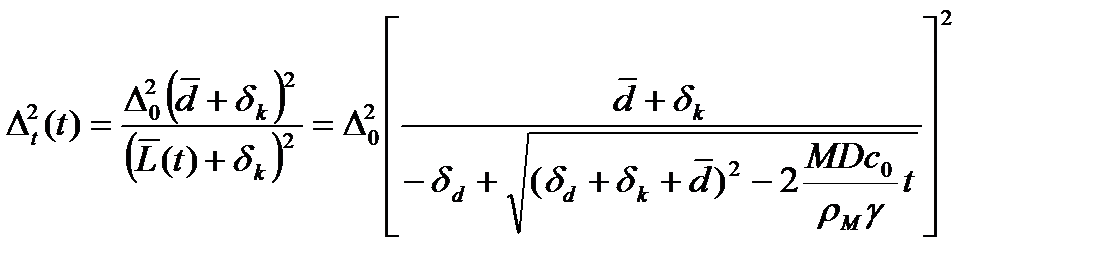. (25)
При определении времени заполнения пор, т.е. времени, соответствующего полному заполнению наиболее коротких пор, будем считать, что наиболее короткие поры имеют длину, отличающуюся от средней длины пор на 3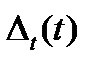 
. При условии, что 
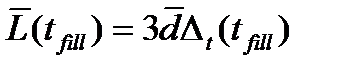, из соотношения (25) получим следующее выражение для определения средней длины пор, соответствующей времени заполнения пор:
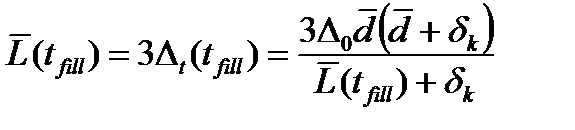. (26)
Из соотношения (26) будем иметь:
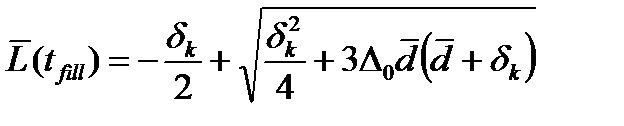. (27)
С учетом соотношения (22) для времени заполнения пор получим следующее выражение:
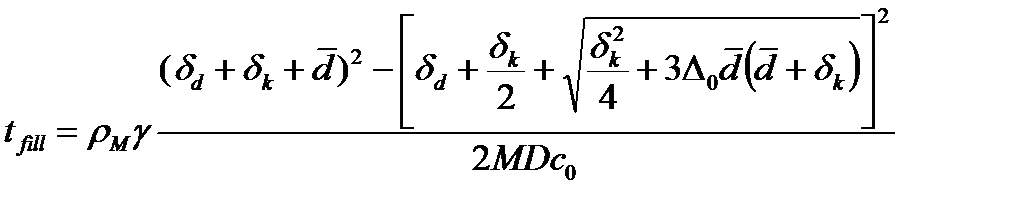. (28)
Определяя степень заполнения пор матрицы следующим образом:
, (29)
с учетом соотношения (27) получим:
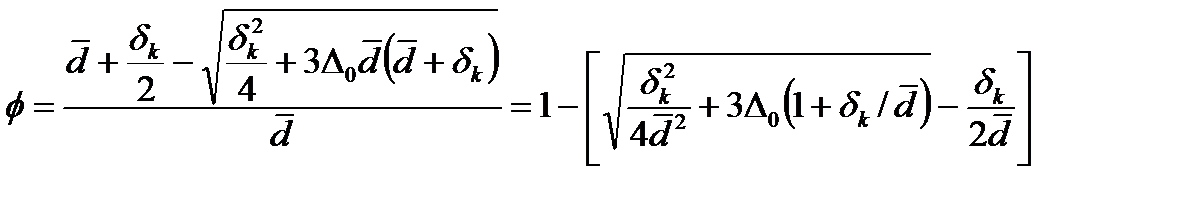. (30)
Полученные соотношения позволяют определить основные закономерности процесса электроосаждения в цилиндрические регулярно расположенные поры
Результаты моделирования
При выполнении расчетов были использованы следующие значения параметров: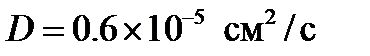 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
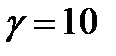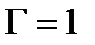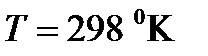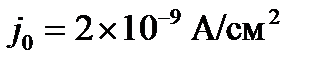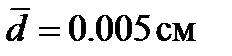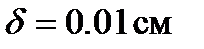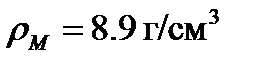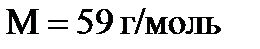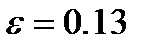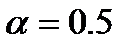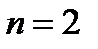, которые близким к условиям проведения экспериментов [31].
Расчеты проводились для двух значений параметра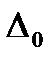 
, характеризующего начальную неравномерность распределения длин пор: 
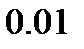и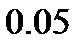 
. В соответствии с правилом 6 сигм для нормального закона распределения принятые значения параметра 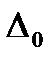соответствуют тому, что большинство пор будут иметь начальную длину в диапазоне: 
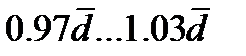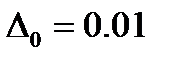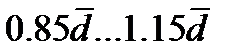- при 
; 
- при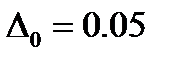 
. Расчеты проводились при различных значениях катодного перенапряжения (от -0.6 В до -1.2 В).
На рис. 3 и рис. 4 представлены зависимости средней плотности тока от времени при начальной неравномерности длин пор, равной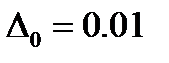 
и 
, при различных перенапряжениях.
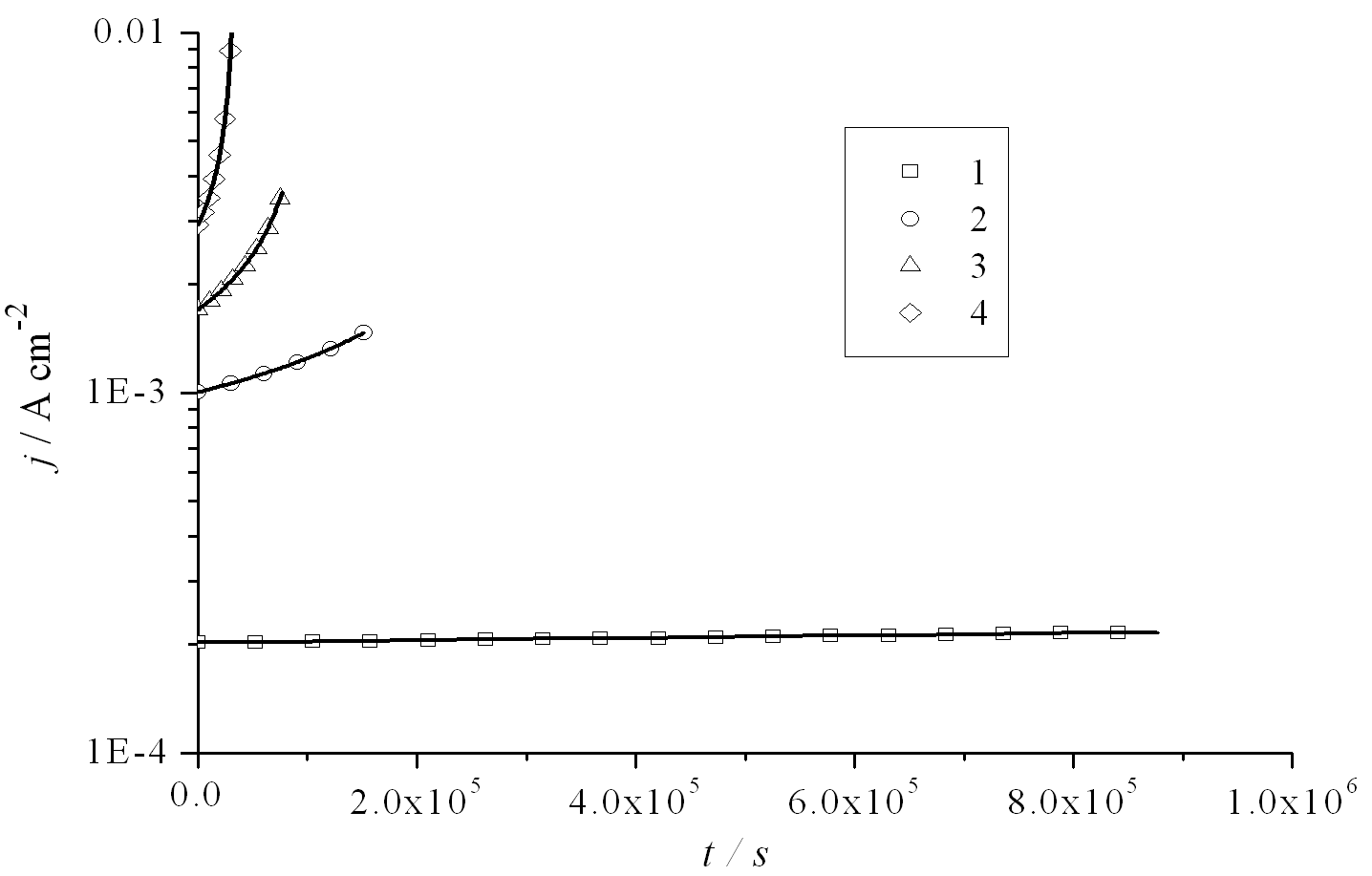
Рисунок 3 - Зависимость средней плотности тока от времени при 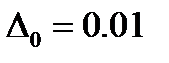и при различных значениях перенапряжения: 1 – η=-0.7 В; 2 – η=-0.8 В;
3 – η=-0.85 В; 4 – η=-1.1 В. Аналитическое решение – сплошная линия, численное решение – символ.
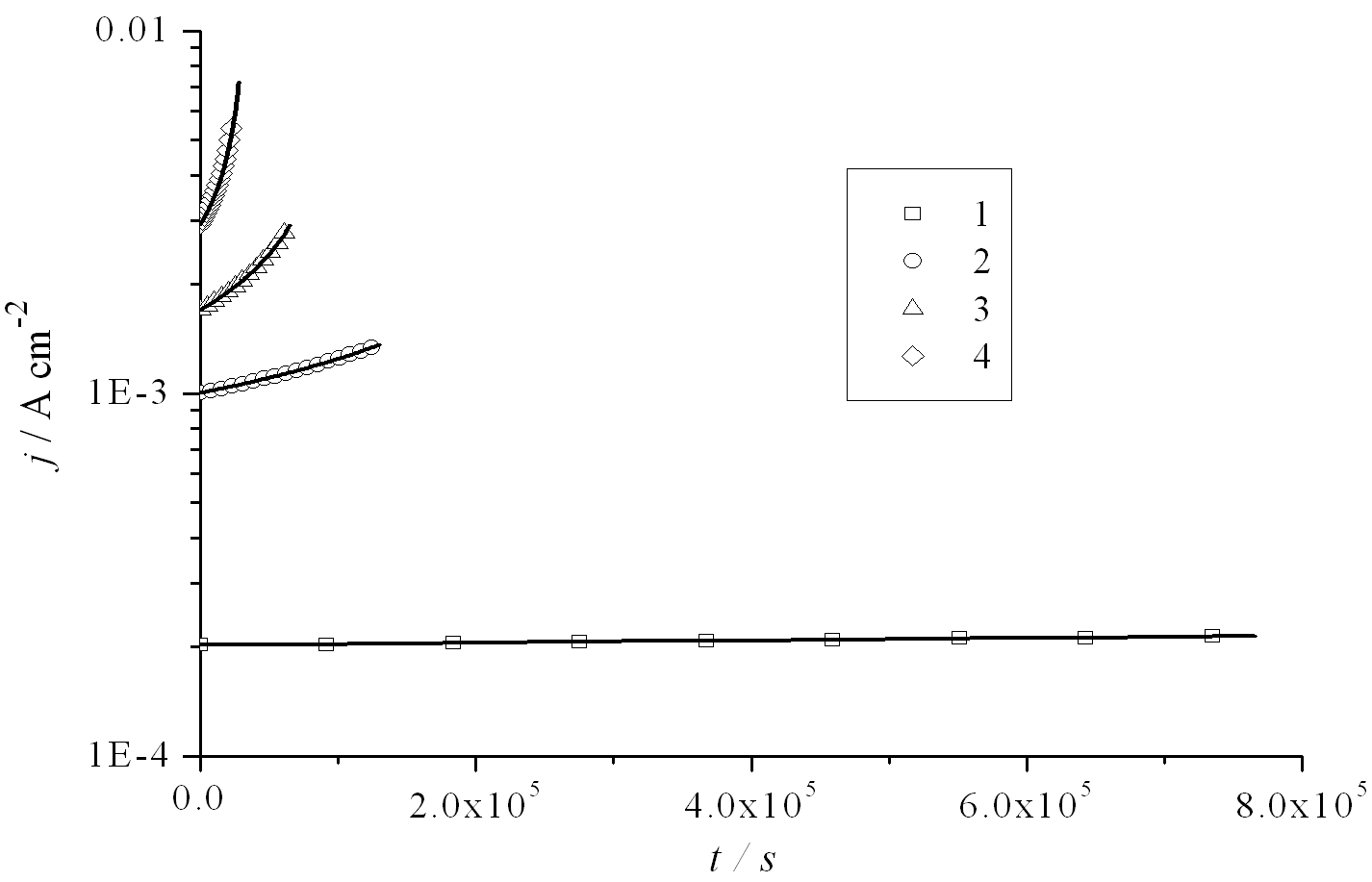
Рисунок 4 - Зависимость средней плотности тока от времени при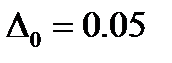 
и при различных значениях перенапряжения: 1 – η=-0.7 В; 2 – η=-0.8 В;
3 – η=-0.85 В; 4 – η=-1.1 В. Аналитическое решение – сплошная линия, численное решение – символ.
Как видно из результатов, представленных на рис. 3 и 4 имеет место очень хорошее совпадение между аналитическим и численным решением для всех рассмотренных значений перенапряжения. Наиболее важное отличие связано с темп, что при аналитическом решении получается несколько больше значение времени заполнения пор. Относительная разность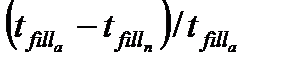 
(где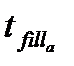 
, 
- время заполнения пор при аналитическом и численном решении, соответственно) увеличивается при увеличении перенапряжения и при увеличении начальной относительной неравномерности длин пор. Так при 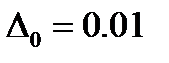значение 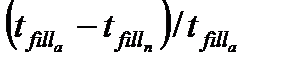равно 0.0858%, 0.1245% 0.2894% и 3.7313% при перенапряжениях -0.7 В, -0.8 В, -0.85 В и -1.1 В, соответственно. При увеличении 
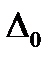до 0.05 соответствующие значения равны: 0.0276%, 0.5437%, 2.4768% и 15.7892%. Таким образом, при сравнительно небольшой неравномерности длин пор целесообразно использовать аналитическое решение, которое обеспечивает достаточно высокую точность решения вплоть до высоких перенапряжений. По мере увеличения степени начальной неравномерности длин пор точность аналитического решения уменьшается, особенно при больших перенапряжениях. При этом в области больших перенапряжений целесообразно использовать численное решение, а при достаточно невысоких перенапряжениях допустимо использовать аналитический метод.
|
|
|
На рис. 5 и 6 представлены зависимости изменения неравномерности длин пор в процессе осаждения металла.
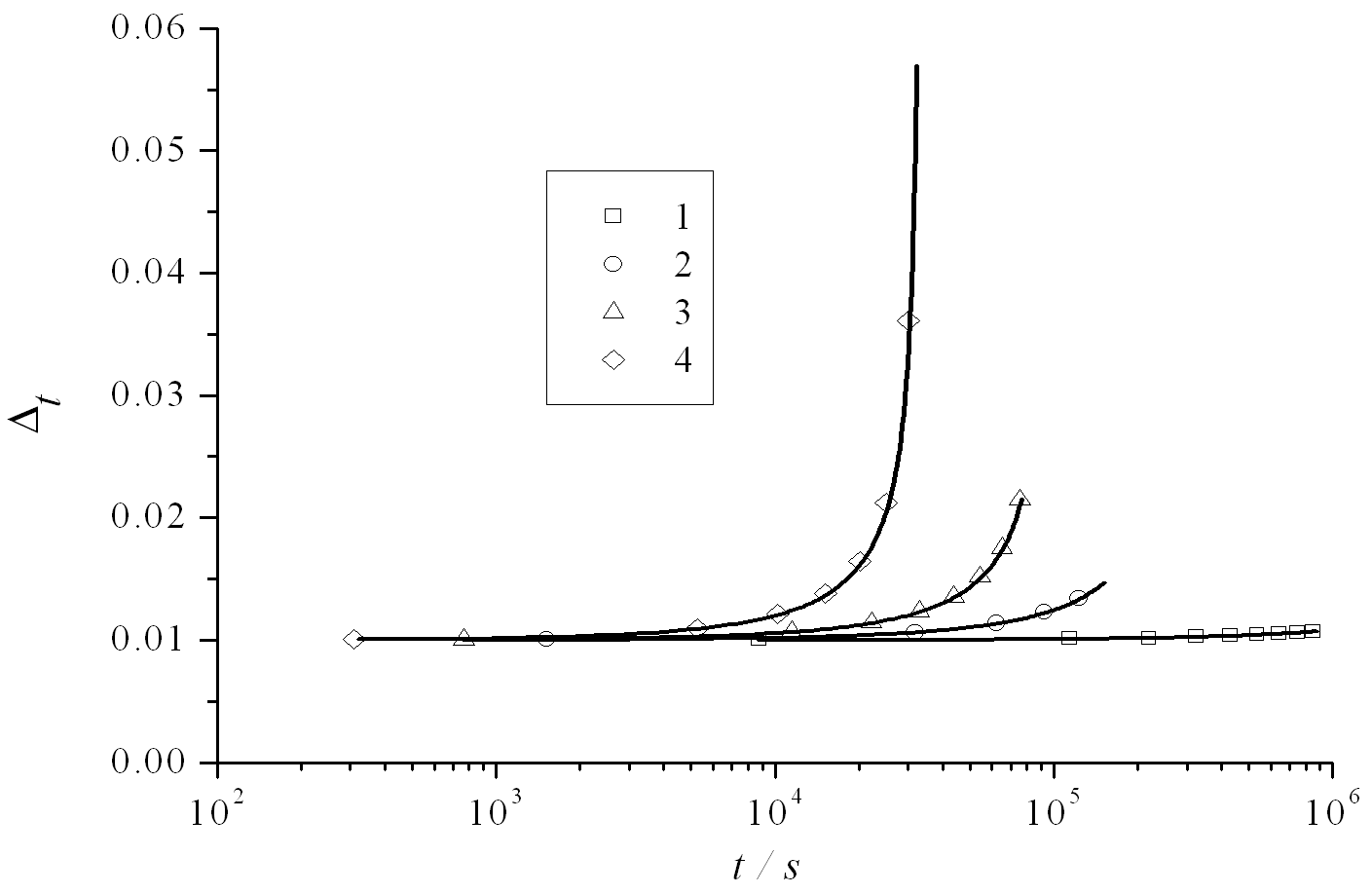
Рисунок 5 - Зависимость неравномерности длин незаполненных частей пор от времени при 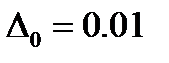и при различных значениях перенапряжения:
1 – η=-0.7 В; 2 – η=-0.8 В; 3 – η=-0.85 В; 4 – η=-1.1 В. Аналитическое решение – сплошная линия, численное решение – символ.
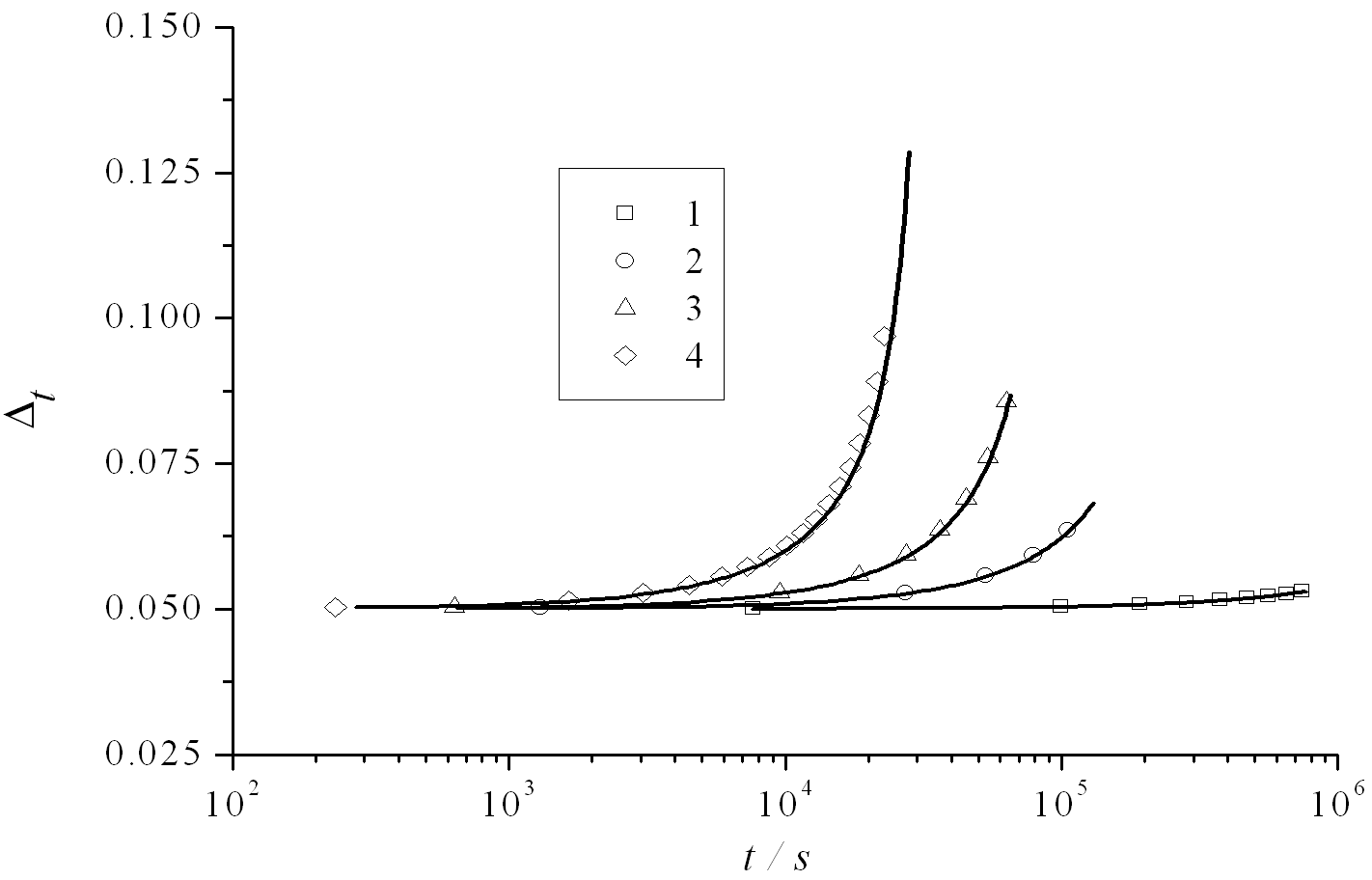
Рисунок 6 - Зависимость неравномерности длин незаполненных частей пор от времени при 
и при различных значениях перенапряжения:
1 – η=-0.7 В; 2 – η=-0.8 В; 3 – η=-0.85 В; 4 – η=-1.1 В. Аналитическое решение – cплошная линия, численное решение – символ.
Здесь, как и для средней плотности тока, имеет место хорошее совпадение аналитического и численного решений во всех рассмотренных случаях. Увеличение степени неравномерности длин незаполненных частей пор в процессе электроосаждения металла оказывает влияние на время заполнения пор и степень заполнения пор металлом (рис. 7).
Рисунок 7 - Зависимость степени заполнения пор 
от перенапряжения при различных начальных отклонениях длин пор от среднего значения:
1 - 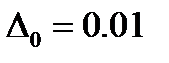, 2 -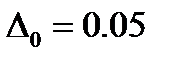 
.
Как видно из рис. 7 при увеличении отклонения потенциала электрода от равновесного значения степень заполнения пор уменьшается, что соответствует результатам численного решения. Кроме того, степень заполнения пор уменьшается при увеличении начальной, а, следовательно, и текущей, неравномерности длин незаполненных частей пор.
Формирование функциональных поверхностей с микро- и нанопараметрами при катодном электроосаждении металлов и сплавов в поры матрицы с переменной пористостью
Постановка задачи
На рис. 8 представлена схема электроосаждения металла в поры матрицы, пористость которой изменяется по ее высоте.
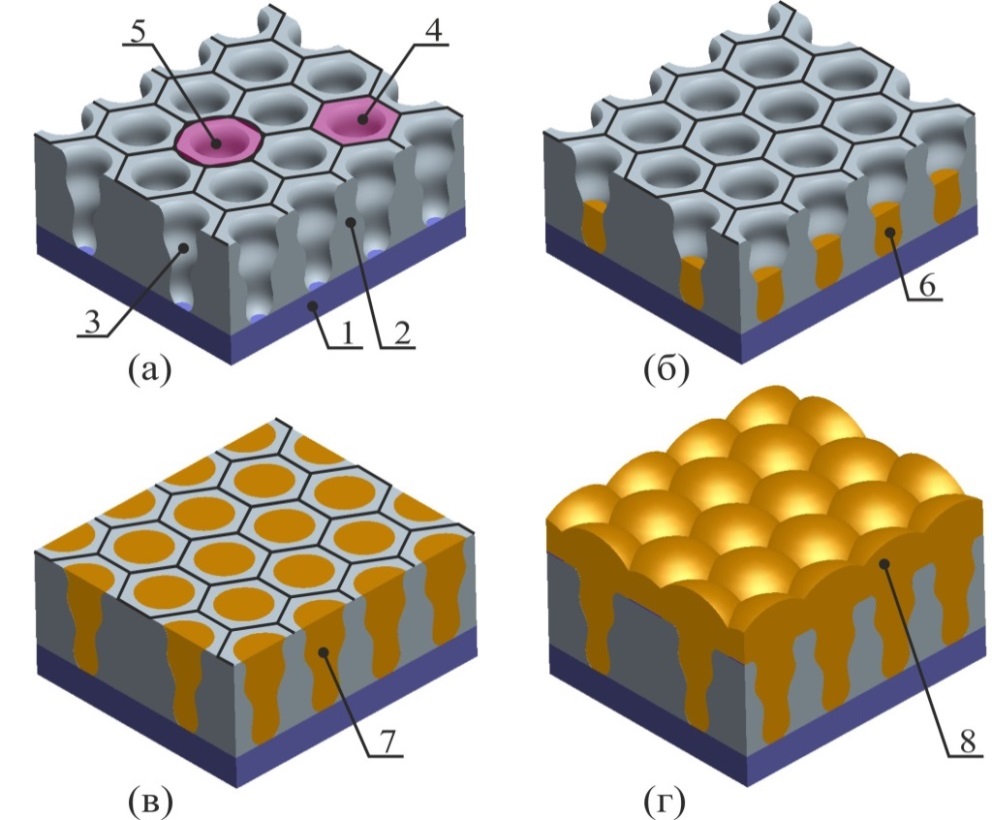
Рисунок 8 - Схема электроосаждения металлы в поры матрицы с переменной пористостью: (а) –матрица до начала электроосаждения; (б) – матрица с частично заполненными порами; (в) – матрица с полностью заполненными порами; (г) – матрица, на поверхности которой сформирован сплошной слой металла; 1 – токопроводящий слой, выполняющий функция токоподвода к катоду; 2 – нанопористая матрица из оксида алюминия; 3 – пора матрицы; 4 – поверхность матрицы, соответствующая поре; 5 – осесимметричная аппроксимация поверхности матрицы, соответствующей поре; 6 – нанопроволочка, частично заполнившая пору; 7 – нанопроволочка, полностью заполнившая пору; 8 – сплошной осадок.
Математическая модель
В модели электроосаждения металла в поры матрицы, имеющей переменную по ее толщине пористость (рис. 9), будут использованы те же допущения, что и при моделировании электроосаждения в цилиндрические поры.
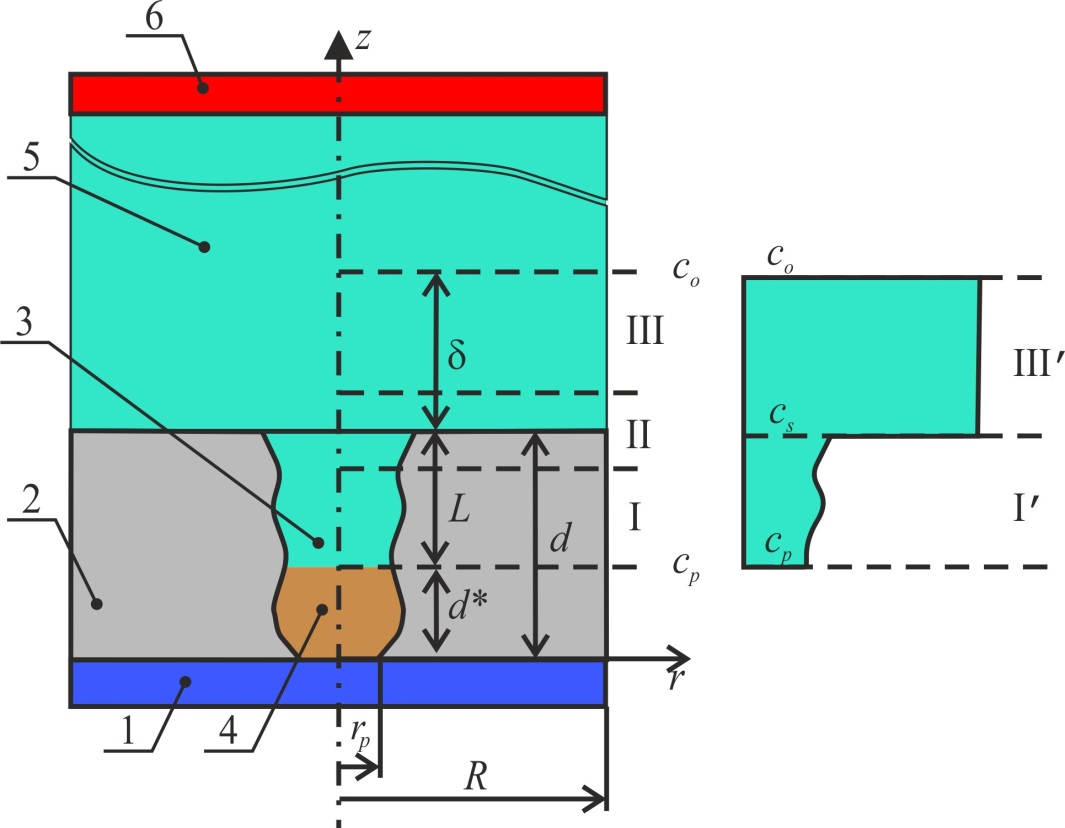
Рисунок 9 - Схема для расчета массопереноса при электроосаждении металла в пору: 1 – проводящий слой (токоподвод); 2 – матрица; 3 – пора; 4 – часть поры, заполненная металлом; 5 – пространство между матрицей и вспомогательным электродом, заполненное раствором электролита;
6 – вспомогательный электрод (анод)
Здесь d – толщина матрицы; d* - текущая толщина осадка в поре; L = d − d*(t) – текущая длина незаполненной части поры; R – радиус осесимметричной области, соответствующей одной поре; d - толщина внешнего диффузионного слоя; c0, cp, и cs – концентрации катионов металла в объеме раствора, на дне поры и в устье поры, соответственно.
В зонах I и III имеет место одномерное распределение концентраций катионов металла, в то время как в переходной зоне II распределение концентраций является двумерным. При решении задачи можно ограничиться рассмотрением только двух зон I’ и III’ с одномерным распределением концентраций катионов металла. При этом влияние переходной зоны может быть учтено с помощью следующего коэффициента:
. (31)
При этом распределение концентраций должно находиться из решения следующей задачи:
(32)
с граничными условиями на внешней границе диффузионного слоя:
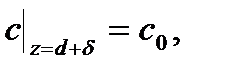(33)
и на внешней поверхности матрицы, которая является неравнодоступной:
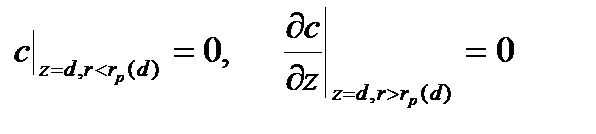. (34)
В одномерном квазистационарном приближении диффузионный перенос электроактивных ионов в порах описывается следующим уравнением:
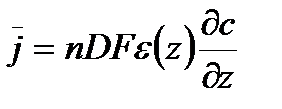(35)
где 
– средняя по поверхности матрицы плотность тока; 
– пористость, изменяющая по высоте матрицы; D – коэффициент диффузии электроактивных катионов; n – валентность электроактивных катионов; F – число Фарадея.
Интегрируя соотношение (35) по всей длине незаполненной поры получим
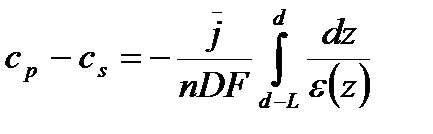(36)
Будем считать, что плотность тока на дне поры связана с перенапряжением электрохимической реакции посредством уравнения Тафеля:
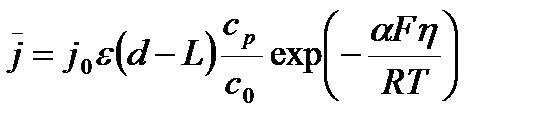,(37)
где 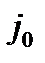- плотность тока обмена, α – коэффициент переноса, R – универсальная газовая постоянная, T - температура.
Используя уравнение (37), можно получить следующее соотношение для концентрации катионов металла на дне поры:
(38)
На основании закона Фарадея имеем:
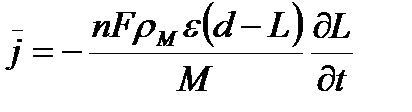(39)
Учитывая, что средняя плотность тока во внешнем диффузионном слое определяется следующим соотношением
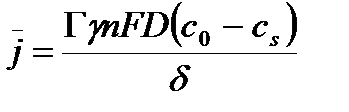(40)
где - отношение значений коэффициента диффузии электроактивного катиона в объеме раствора электролита и в поре.
Подставляя (40) в (36) получим выражение для концентрации в устье поры:
(41)
Подставляя полученное выражение в (11) получим уравнение для определения плотности тока:
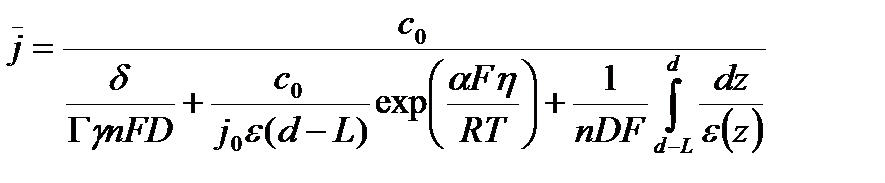(42)
С использованием соотношений (42), (38) и (41) можно определить зависимости изменения плотности тока, концентраций на дне и в устье поры от времени.
Подставляя соотношение (42) в уравнение (39) получим соотношение для определения длины незаполненной части поры:
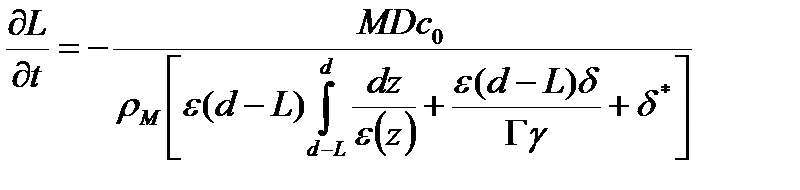(43)
где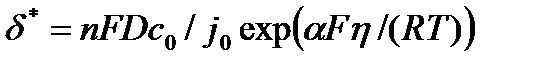 
- параметр, учитывающий кинетику электрохимической реакции.
При решении уравнения (43) должно быть использовано следующее начальное условие:
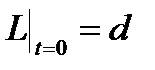. (44)
При 
из соотношения (43) получим уравнение [50]
(45)
Для решения уравнения (43) нужно задать закон изменения пористости по длине поры (толщине матрицы). Рассмотрим несколько различных вариантов изменения пористости по толщине матрицы.
1. Цилиндрическая пора ()
Уравнение (45) легко интегрируется, в результате имеем следующее аналитическое выражение для зависимости длины незаполненной части поры от времени:
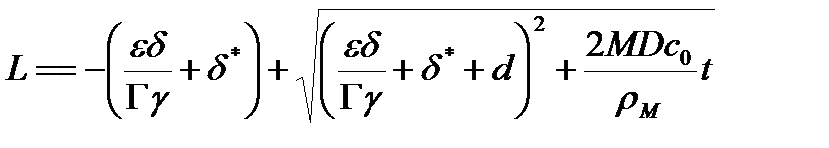(46)
2. Коническая пора (
) (в зависимости от знака 
диаметр поры по ее длине может уменьшаться или увеличиваться).
Используя аналитическое выражение для интеграла 
, соотношение (43) можно записать в следующем виде:
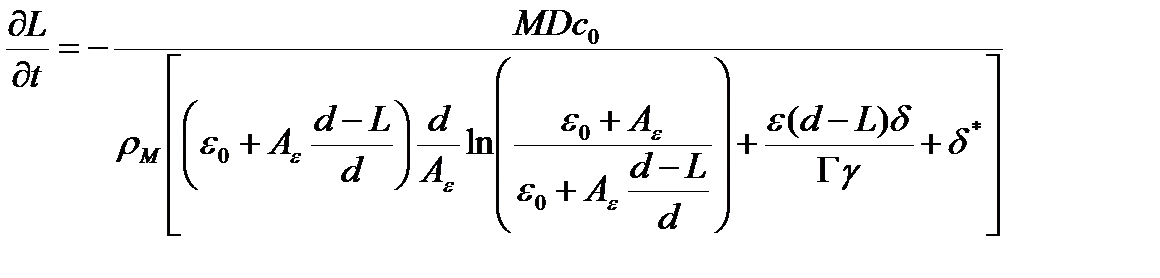(47)
Решение уравнения (47) может быть выполнено с использованием численных методов.
3. Пора с периодически изменяющимся диаметром (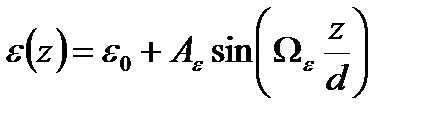
)
Используя аналитическое выражение для интеграла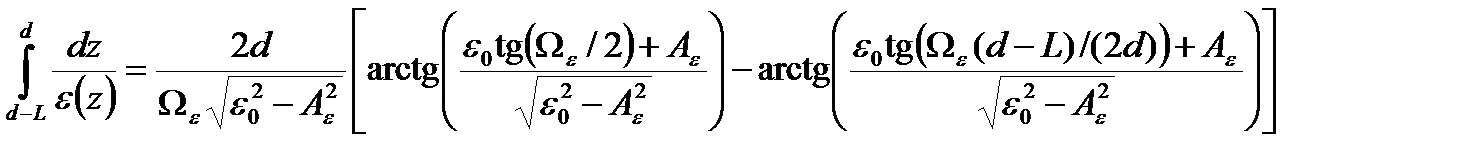 
, соотношение (43) можно записать в следующем виде:
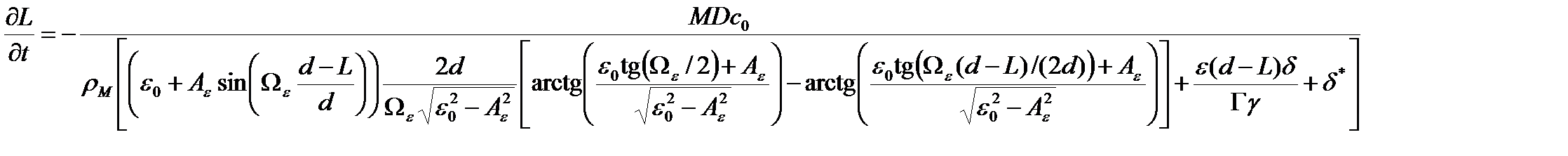(48)
Уравнение (48), так же как и уравнение (47), может быть решено численно.
При численном решении уравнение (43) удобнее записать в следующем виде
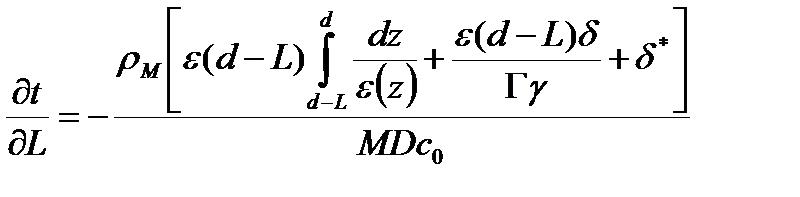(49)
При численном решении уравнения (49) будем задавать постоянный шаг по L и рассчитывать соответствующие значения времени с помощью следующего разностного уравнения:
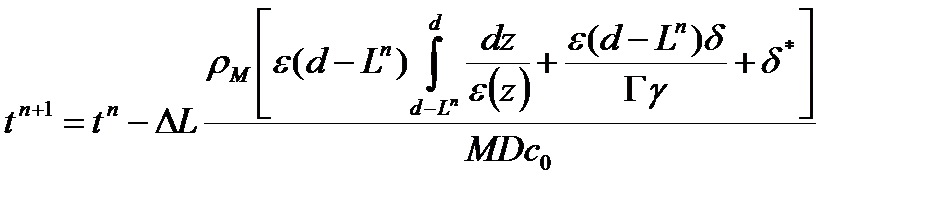(50)
где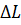 
– шаг по глубине поры.
Результаты моделирования
При выполнении расчетов были использованы следующие значения параметров: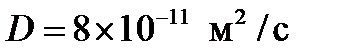 
, 
, , , 
, 
, 
, 
, 
, 
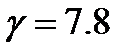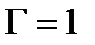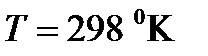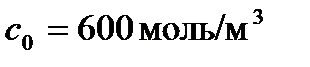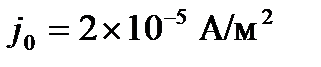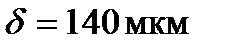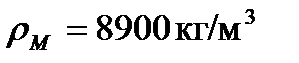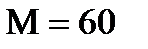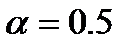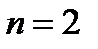, , , которые близким к условиям проведения экспериментов [31].
На рис. 10 представлены зависимости изменения длины незаполненной части поры от времени при перенапряжении равном -1.1 В для четырех различных законов изменения пористости матрицы по ее толщине. Из полученных результатов следует, что при уменьшении пористости по толщине матрицы скорость роста нанопроволочек уменьшается, и, наоборот, при увеличении пористости матрицы по ее толщине – скорость роста нанопроволочек увеличивается. Это объясняется тем, что в первом случае в процессе заполнения пор средняя пористость незаполненных частей пор с течением времени уменьшается, а, следовательно, увеличивается сопротивление диффузионному переносу ионов. Во втором случае наблюдается обратная картина – средняя пористость в процессе электроосаждения увеличивается, а сопротивление диффузионному переноса электроактивных ионов уменьшается. Интересно, что при периодическом изменении пористости матрицы (кривая 4 на рис. 10) общее время заполнения пор матрицы увеличивается.
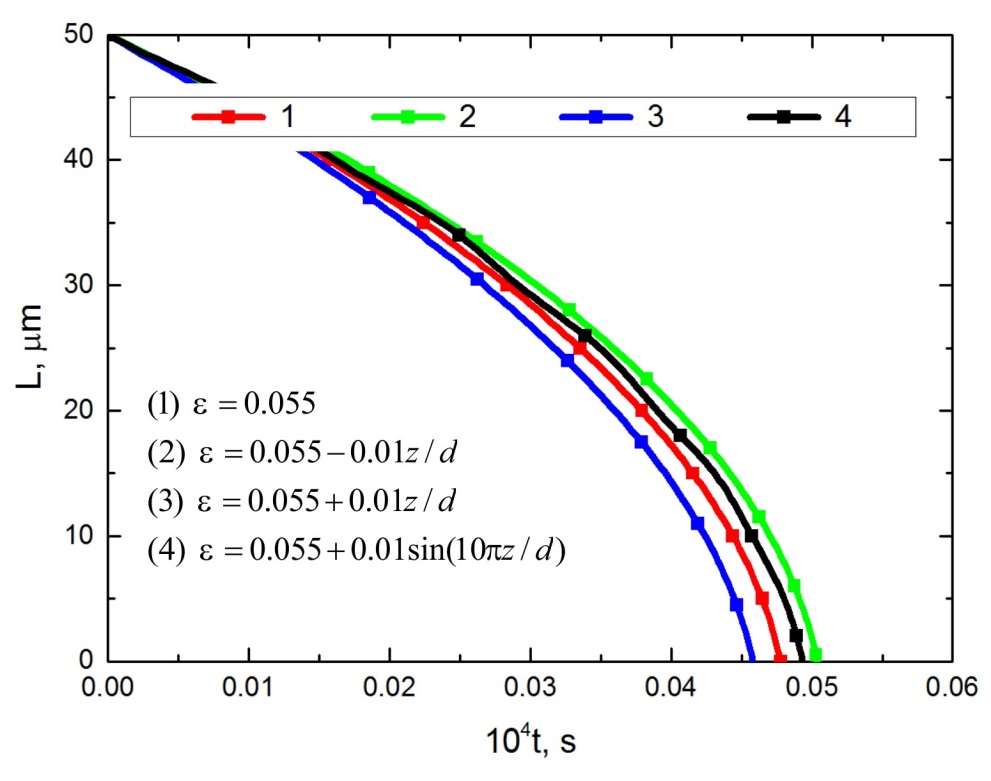
Рисунок 10 - Зависимость длины незаполненной части пор от времени при перенапряжении h = −1.1 В
На рис. 11 представлены зависимости изменения плотности тока от времени при разных значениях перенапряжения для тех же законом изменения пористости, что и на рис. 10. При меньшем перенапряжении (рис. 11 а) изменение пористости хотя и оказывает влияние на величину плотности тока – при увеличении средней пористости незаполненной части поры плотность тока увеличивается, но влияние это сравнительно мало. Относительное изменение плотности тока имеет такой же порядок, что и относительное изменение пористости. Для рассматриваемых случаев относительное изменение плотности тока не превышает 25 %. При увеличении перенапряжения до −1.1 В влияние изменения пористости на плотность тока значительно усиливается (рис. 11 б) – относительное изменение плотности тока может достигать 100 % и более.
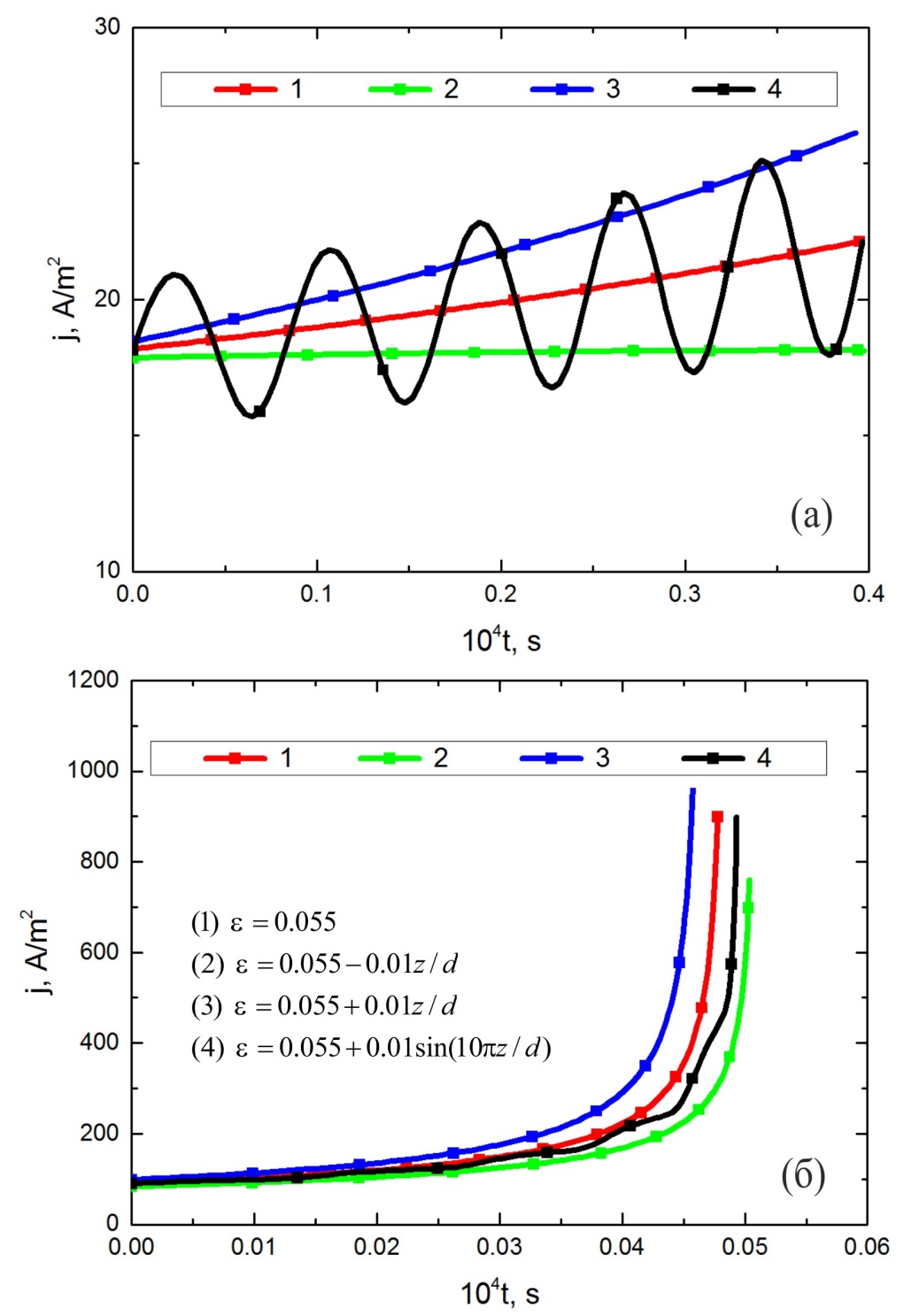
Рисунок 11 - Зависимости плотности тока от времени при различном перенапряжении: (а) h = −0.9 В, (б) h = −1.1 В
На рис. 12 представлены зависимости концентрации электроактивного катиона на поверхности растущего осадка от времени при разных значениях перенапряжения для тех же законом изменения пористости, что и на рис. 10. При меньшем перенапряжении (рис. 12 а) концентрация катионов на поверхности осадка в начале процесса электроосаждения отличается от концентрации в объеме раствора электролита приблизительно на 20 %. В процессе заполнения пор металлом концентрация катионов увеличивается, так как уменьшаются диффузионные ограничения, и в конце заполнения пор матрицы приближается к объемному значению.
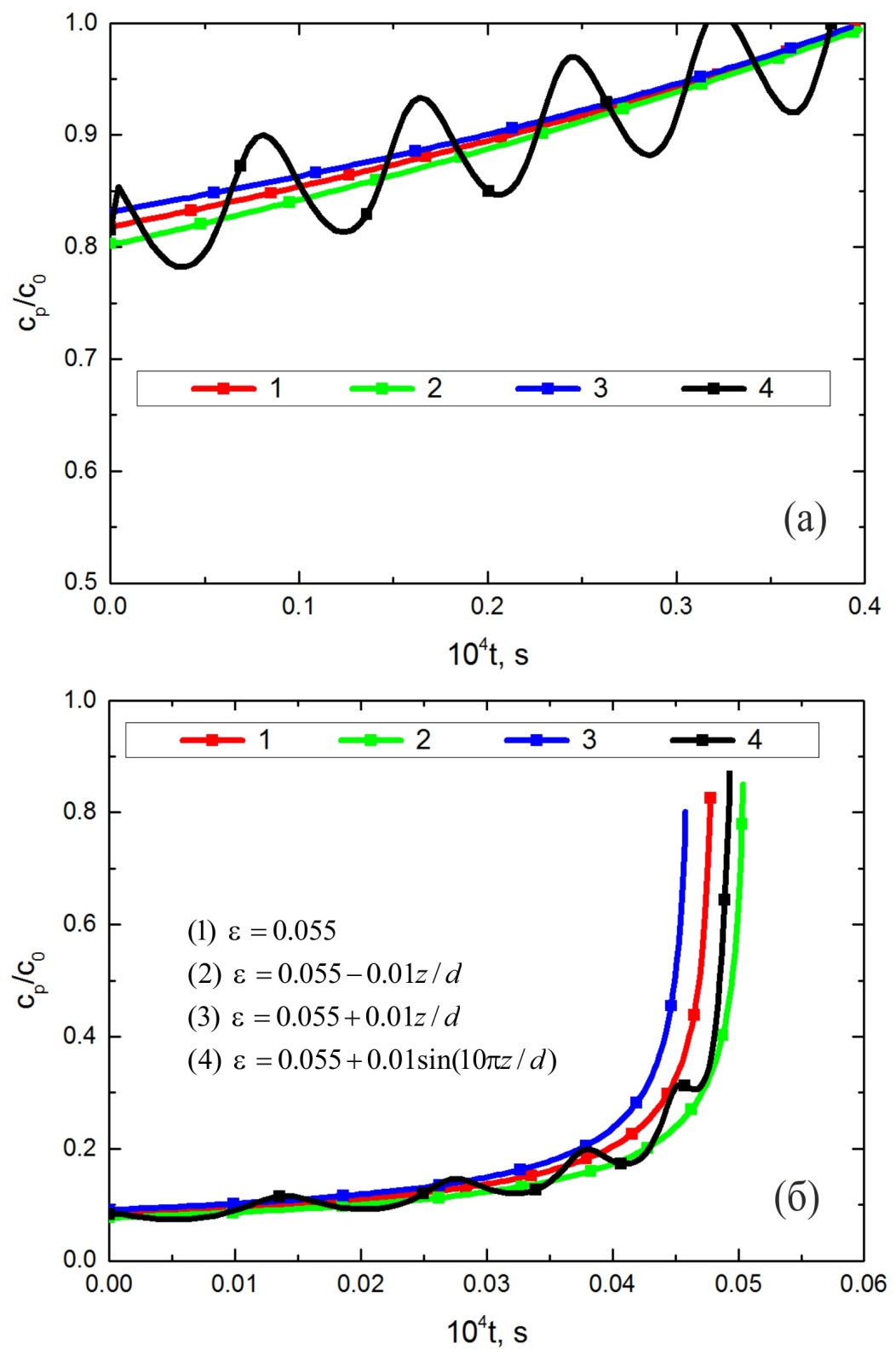
Рисунок 12 - Зависимости концентрации электроактивного катиона на поверхности растущего осадка от времени при различном перенапряжении: (а) – η=-0.9 В; (б) – η=-1.1 В
При большем перенапряжении (рис. 12 б) в начальный период роста нанопроволочек концентрация катионов на дне поры примерно в десять раз отличается от объемного значения. С течением времени длина незаполненной части поры уменьшается и диффузионные ограничения, частично снимаются, поэтому концентрация катионов увеличивается, однако даже на конечном этапе заполнения пор она не достигает объемного значения.
|
|
|
