Формирование функциональных поверхностей с микро- и нанопараметрами при катодном электроосаждении металлов и сплавов через маску из монослойного коллоидного кристалла

 

3.1 Постановка задачи

На рис. 13 представлена схема электроосаждения металла с использованием в качестве маски однослойного коллоидного кристалла. Принимая во внимание расположение частиц в маске, будем использовать единичную ячейку с сечением в виде правильного шестиугольника (рис. 14a). В качестве верхней (внешней) границы единичной ячейки примем плоскость, удаленную от маски на достаточно большое расстояние, так что в этой плоскости распределение плотности тока можно считать однородным. В качестве нижней границы единичной ячейки примем поверхность растущего осадка металла. Без большой погрешности единичная ячейка может быть приближенно заменена осесимметричной (рис. 14б).

 

3.2 Математическая модель

В качестве математической модели будем использовать уравнение Лапласа для потенциала электрического поля в растворе электролита (51) и уравнение эволюции обрабатываемой поверхности (52):

(51)

(52)

где - потенциал; x, y, z – координаты; z _c – функция, описывающая поверхность осадка; t – время; - выход по току; - объемный электрохимический эквивалент; - удельная электропроводность раствора электролита; N - единичный вектор внешней нормали к поверхности

 

Рисунок 13 - Схема электроосаждения металла через маску из однослойного коллоидного кристалла: (а) металлическая подложка с маской до начала обработки; (б) металлическая подложка с маской в процессе обработки;

(в), (г) поверхность осадка металла после удаления маски; (в) толщина осадка меньше радиуса сферических частиц; (г) толщина осадка равна радиусу сферических частиц

 

 

 

Рисунок 14 - Расположение сферических частиц в маске из коллоидного кристалла и единичная ячейка с поперечным сечением в виде правильного шестиугольника (а) и осесимметричная аппроксимация единичной ячейки (б)

 

Для удобства численного решения и анализа полученных результатов математическая модель была приведена к безразмерному виду. При переходе к безразмерным переменным, диаметр сферических частиц был принят в качестве единицы длины, а приложенное значение плотности тока было принято в качестве единицы плотности тока:

(53)

где X, Y, Z – безразмерные координаты; Z _c – безразмерная функция, описывающая поверхность растущего осадка; - безразмерный потенциал; h – высота единичной ячейки; H – безразмерная высота единичной ячейки.

Безразмерное время было определено следующим образом:

(54)

В безразмерных переменных математическая модель может быть представлена в следующем виде:

(55)

(56)

В качестве граничных условий будем использовать следующие соотношения:

(57)

где C – нижний индекс, который обозначает поверхность осадка; U - нижний индекс, который обозначает внешнюю поверхность единичной ячейки; I - нижний индекс, который обозначает боковые поверхности единичной ячейки и поверхность сферической частицы.

В качестве начального условия примем:

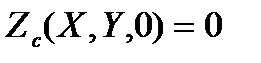, (58)

что соответствует исходной плоской поверхности металлической подложки.

 

При моделировании будем использовать квазистационарное приближение, в соответствии с которым при расчете распределения потенциала не учитывается движение поверхности подложки вследствие электроосаждения металла, а при расчете эволюции обрабатываемой поверхности используется распределение потенциала, полученное на предыдущем шаге. Таким образом, на каждом шаге по времени:

- рассчитывается распределение плотности тока в единичной ячейке в результате решения уравнения Лапласа;

- определяется новое положение поверхности металлического осадка в результате решения уравнения (56).

Для численного решения уравнения Лапласа использовался метод граничных элементов, важным достоинством которого является простота перестроения сетки при изменении геометрии расчетной области в результате анодного растворения подложки. При этом уравнение Лапласа сводилось к граничному интегральному уравнению:

(59)

Численное решение уравнения (59) осуществлялось обычным методом граничных элементов (объем вычислений от N ² до N ³ в зависимости от метода решения системы линейных алгебраических уравнений)

(60)

где .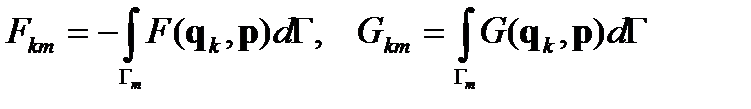

Обычный метод граничных элементов не позволяет использовать достаточно мелкие сетки, обеспечивающие достаточную точность расчета распределения потенциала, поэтому также был использован быстрый мультипольный метод граничных элементов (объем вычислений от N дo N ² в зависимости от метода решения системы линейных алгебраических уравнений). В случае использования быстрого мультипольного метода граничных элементов коэффициенты системы разностных уравнений определялись с использованием следующих соотношений:

(61)

где ; - базовая точка разложения; - координаты точки в сферической системе координат; - ассоциированная функция Лежандра; .

Для численного решения уравнения эволюции обрабатываемой поверхности был использован метод “Level Set”. Разностная форма уравнения (6) на сетке из равносторонних треугольных элементов может быть записана в следующем виде:

(62)

где k – номер расчетной точки; n – номер шага по времени; - безразмерный шаг по времени.

Значения производных по пространственным координатам в соотношении (62) рассчитывались с использованием следующих соотношений:

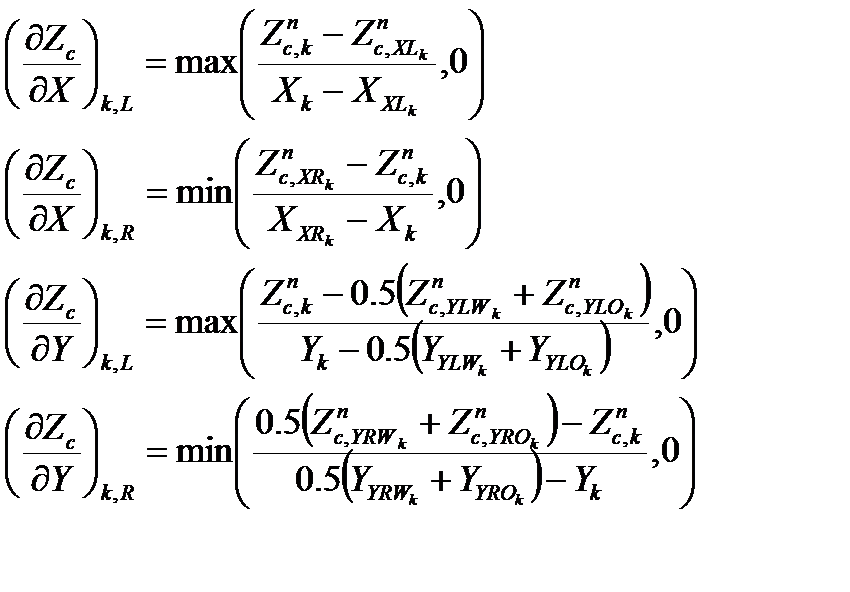(63)

Соотношения (63) являются обобщением известных соотношений метода “Level Set” для конечно-разностной сетки: в случае сетки из равносторонних треугольных элементов для аппроксимации производных по оси X можно непосредственно использовать соотношения для конечно-разностной сетки, в то время как, для аппроксимации производных по оси Y требуется использовать среднее значение для двух соседних узлов.

После каждого шага по времени производилась перестроение сетки на боковых поверхностях расчетной области.

 

3.3 Результаты моделирования

Численное решение краевой задачи (55), (57) было выполнено методом граничных элементов. Параметры сетки были выбраны так, чтобы расчетные результаты были независимы от шага сетки и номера вершин. Было установлено, что в зависимости от степени упаковки сферических частиц (безразмерного радиуса сферических частиц R), необходимо использовать сетку, содержащую от 5000 до 20000 граничных элементов (рис. 15).

 

Рисунок 15 - Схема разбиения границы расчетной области на граничные элементы: (а) R=0.1; (б) R=0.25; (в) R=0.5

На поверхностях, соответствующих осадку металла и внешней границе расчетной области, формировались граничные элементы в виде равносторонних треугольников. На боковых поверхностях расчетной области использовались граничные элементы в виде прямоугольных треугольников, причем для исключения влияния сетки на распределение потенциала высота элементов уменьшалась по мере приближения к обрабатываемой поверхности.

На втором этапе осуществлялось моделирование роста осадка металла при различной степени упаковки сферических частиц (рис. 16).

 

Рисунок 16 - Результаты моделирования электроосаждения металла через МКК-маску при различных радиусах сферических частиц: (а, г, ж) R=0.1; (б, д, з) R=0.25; (в, е, и) R=0.5; (а, б, в) перед электролитическим осаждением; (г, д, е) при толщине осадка, равной 0.4R; (ж, з, и) при толщине осадка, равной 0.8R

 

В процессе катодного осаждения на обрабатываемой поверхности формируются нановыступы, форма которых близка к осесимметричной. Причем при уменьшении степени упаковки сферических частиц (при уменьшении R) отклонение от осесимметричности также уменьшается. Высота нановыступов увеличивается с течением времени (рис. 17).

 

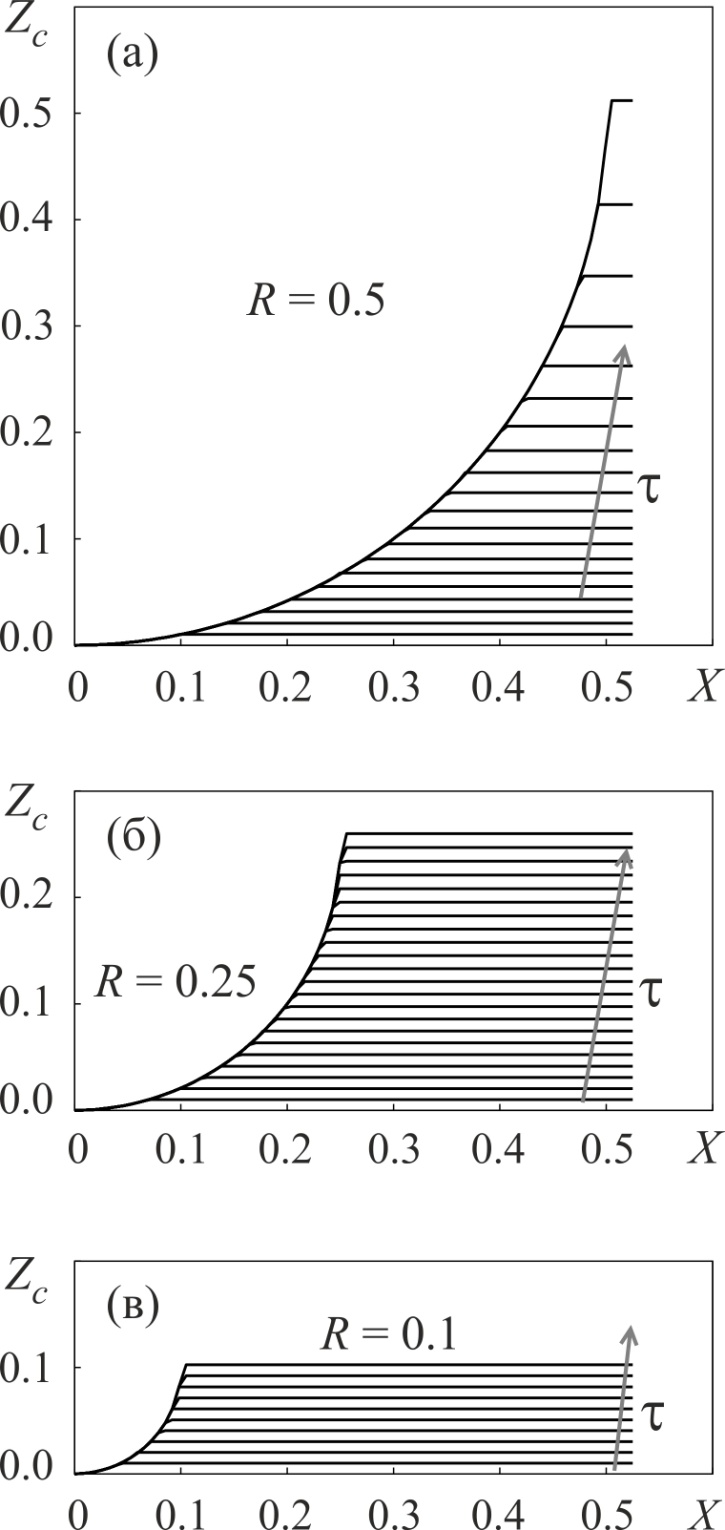
Рисунок 17 - Результаты моделирования электроосаждения металла через МКК маску в рамках осесимметричного приближения при различном радиусе сферических частиц: (а) R =0.5; (б) R =0.25; (в) R =0.1

 

Полученные в результате моделирования зависимости потенциала (ток) от толщины осадка хорошо согласуются с экспериментальными данными: потенциал увеличивается (ток уменьшается) с уменьшением электроактивной площади поверхности. Относительная амплитуда токовых колебаний зависит от отношения средней плотности тока к предельной плотности тока для электрода через коллоидную маску: относительная амплитуда токовых колебаний уменьшается, когда средний ток приближается к предельному значению.

Ввиду факта, что поверхность осадка в единичной ячейке можно считать осесимметричной, численные эксперименты были выполнены в пределах осесимметричного приближения. Это позволило существенно сократить объем вычислений. На рис. 6 представлены результаты моделирования для сферических частиц с различным радиусом. Стрелка на рис. 17 показывает направление увеличение времени с шагом Δτ = 0.01. В случае необходимости размерное время может быть определено уравнением (4).

В случае плотно упакованных сферических частиц (R= 0.5 ) скорость осаждения увеличивается наиболее круто (рис. 6а), тогда как в случае низкой плотности упаковки частиц (R= 0.1 ), скорость осаждения незначительно увеличивается с увеличением толщины осадка (Рис. 6в).

Полученные в результате моделирования зависимости потенциала от толщины осадка хорошо согласуются с экспериментальными данными: потенциал увеличивается с уменьшением электроактивной площади поверхности.

 

ЗАКЛЮЧЕНИЕ

 

В результате выполнения второго этапа разработаны математические модели и методы численного моделирования формирования функциональных поверхностей с микро- и нанопараметрами при электрохимическом осаждении металлов и сплавов с использованием матриц, имеющих поры разного типа. При моделировании определены формы и размеры единичных ячеек, произведен учет поляризации электродов и зависимости выхода по току от плотности тока. В частности были получены:

- аналитическое и численное решения задачи электроосаждения металла в регулярно расположенные цилиндрические поры, начальная длина которых различна и подчиняется нормальному закону распределения;

- численное решение задачи электроосаждения металла в регулярно расположенные поры матрицы, пористость которой изменяется по ее толщине;

- численное решение задачи электроосаждения металла в поры матрицы из монослойного коллоидного кристалла.

Разработанные алгоритмы и реализующее их программное обеспечение могут быть использованы при проектировании процессов катодного осаждения при создании наноструктурированных поверхностей, а также для оптимизации условий проведения процесса.

Задачи второго этапа, сформулированные в техническом задании, выполнены в полном объеме. Полученные при выполнении работы результаты [52 – 67] являются новыми и соответствуют мировому уровню, что, в частности, подтверждается наличием публикаций, индексируемых в Web of Science, и включением в программы ряда престижных международных конференций.

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Bruzzone A.A.G. Advances in engineered surfaces for functional performance / A.A.G. Bruzzone, H.L.Costa, P.M.Lonardo, D.A. Lucca // CIRP Annals-Manufacturing Technology. - 2008. - V.57(2). - P.750-769.

2. De Chiffre L. Surfaces in precision engineering, microengineering and nanotechnology / L.De Chiffre, H.Kunzmann, G.N.Peggs, D.A. Lucca // CIRP Annals-Manufacturing Technology. - 2003. - V.52(2). - P.561-577.

3. Malshe A. Bio-inspired functional surfaces for advanced applications / A. Malshe, K. Rajurkar, A. Samant, H.N. Hansen, S. Bapat, W.J iang // CIRP Annals-Manufacturing Technology. - 2013. - V.62(2). - P.607-628.

4. Xia Y. One-Dimensional Nanostructures: Synthesis, Characterization, and Applications / Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim, H. Yan // Advanced Materials. - 2003. - V.15(5). - P.353-389.

5. Li X.M. What do we need for a superhydrophobic surface? A review on the recent progress in the preparation of superhydrophobic surfaces / X.M. Li, D. Reinhoudt, M. Crego-Calama // Chemical Society Reviews. - 2007. - V.36(8). - P.1350-1368.

6. Zhang J. Fabrication and use of artificial superhydrophilic surfaces / J. Zhang, S.J. Severtson // Journal of Adhesion Science and Technology. - 2014. -V.28(8-9). - P.751-768.

7. Yao L. Recent progress in antireflection and self-cleaning technology - From surface engineering to functional surfaces / L. Yao, J. He // Progress in Materials Science. - 2014. - V.61. - P.94-143.

8. Xia Y. Unconventional methods for fabricating and patterning nanostructures / Y. Xia, J.A. Rogers, K.E. Paul, G.M. Whitesides // Chemical Reviews. - 1999. - V.99(7). - P.1823-1848.

9. Huczko A. Template-based synthesis of nanomaterials / A. Huczko // Applied Physics A: Materials Science & Processing. - 2000. - V.70(4). - P.365-376.

10. Wade T.L. Template synthesis of nanomaterials / T.L. Wade, J.-E. Wegrowe // The European Physical Journal Applied Physics. - 2005. - V.29(1). - P.3-22.

11. Velev O.D. Colloidal crystals as templates for porous materials / O.D. Velev, A.M. Lenhoff // Current opinion in colloid & interface science. - 2000. - V.5. - P.56-63.

12. Stein A. Sphere templating methods for periodic porous solids / A. Stein // Microporous and Mesoporous Materials. - 2001. - V.44-45. - P.227-239.

13. Zhang J. Colloidal Self‐Assembly Meets Nanofabrication: From Two‐Dimensional Colloidal Crystals to Nanostructure Arrays / J. Zhang, Y. Li, X. Zhang, B. Yang // Advanced Materials. - 2010. - V.22(38). - P.4249-4269.

14. Ye X. Two-dimensionally patterned nanostructures based on monolayer colloidal crystals: controllable fabrication, assembly, and applications / X. Ye, L. Qi // Nano Today. - 2011. - V.(6). - P.608-631.

15. Jiang P. Large-scale fabrication of periodic nanostructured materials by using hexagonal non-close-packed colloidal crystals as templates / P. Jiang // Langmuir. - 2006. - V.22(9). - P.3955-3958.

16. Searson P.C. Electrochemical processing of metallic nanowire arrays and nanocomposites / P.C. Searson, R.C. Cammarata, C.L. Chien // Journal of Electronic Materials. – 1995. - V.24(8). – P.955-960.

17. Nagaura T. Fabrication of ordered Ni nanocones using a porous anodic alumina template / T. Nagaura, F.Takeuchi, Y. Yamauchi, K. Wada, S. Inoue // Electrochemistry Communications. -2008. – V.10(5). – P.681-685.

18. Proenca M.P. Ni growth inside ordered arrays of alumina nanopores: enhancing the deposition rate / M.P. Proenca, C.T. Sousa, J. Ventura, M. Vazquez, J.P. Araujo // Electrochimica Acta. - 2012. - V.72. - P.215-221.

19. Xu C.-L. Electrodeposition and magnetic properties of Ni nanowire arrays on anodic aluminum oxide/Ti/Si substrate / C.-L. Xu, H. Li, G.-Y. Zhao, H.-L. Li // Applied Surface Science. – 2006. – V.253(3). – P.1399-1403.

20. Xu C.-L. Highly ordered MnO₂ nanowire array thin films on Ti/Si substrate as an electrode for electrochemical capacitor / C.-L. Xu, S.-J. Bao, L.-B. Kong, H. Li, H.-L. Li // Journal of Solid State Chemistry. – 2006. –V.179(5). – P.1351-1355.

21. Li L. Synthetic control of large-area, ordered bismuth nanowire arrays / L. Li, Y. Zhang, G. Li, X. Wang, L. Zhang // Materials Letters. – 2005. – V.59(10). – P.1223-1226.

22. Xu J. Fabrication and magnetic property of monocrystalline cobalt nanowire array by direct current electrodeposition / J. Xu, X. Huang, G. Xie, Y. Fang, D. Liu // Materials Letters. – 2005. – V.59(8). – P.981-984.

23. Cherevko S. Electrodeposition of three-dimensional porous silver foams / S. Cherevko, X. Xing, C.-H. Chung // Electrochemistry Communications. – 2010. – V.12(3). – P.467-470.

24. Jia C. Single crystal Ag₇Te₄ nanowire arrays prepared by DC electrodeposition from aqueous solution / C. Jia, B.Zhang, W. Liu, L. Yao, W. Cai, X. Li // Journal of crystal growth. – 2005. V.285(4). – P.527-533.

25. WangQ. Electrochemical template synthesis of large-scale uniform copper selenides nanowire arrays / Q. Wang // Materials Letters. -2009. V.63(17). – P.1493-1495.

26. Yang Y.W. Template-based fabrication and electrochemical performance of CoSb nanowire arrays / Y.W. Yang, Y.B.Chen, F. Liu, X.Y. Chen, Y.C. Wu // Electrochimica Acta. – 2001. – V.56(18). – P.6420-6425.

27. Wang X.W. (110) Orientation growth of magnetic metal nanowires with face-centered cubic structure using template synthesis technique / X.W. Wang, Z.H. Yuan, J.S. Li // Materials Characterization. – 2011. – V.62(6). – P.642-646.

28. Chen Y. Orientation-controllable growth of Sb nanowire arrays by pulsed electrodeposition / Y. Chen, Y.Yang, X. Chen, F. Liu, T. Xie // Materials Chemistry and Physics. – 2011. – V.126(1). – P.386-390.

29. Liu H. Wang Electrodeposited highly-ordered manganese oxide nanowire arrays for supercapacitors / H. Liu, B. Lu, S. Wei, M. Bao, Y. Wen, F. Wang // Solid State Sciences. – 2012. – V.14(7). – P.789-793.

30. Chu S.Z. Fabrication of integrated arrays of ultrahigh density magnetic nanowires on glass by anodization and electrodeposition / S.Z. Chu, S. Inoue, K. Wada, K. Kurashima // Electrochimica Acta. – 2005. - V.51(5). – P.820-826.

31. Napolskii K.S. Tuning the microstructure and functional properties of metal nanowire arrays via deposition potential / K.S. Napolskii, I.V. Roslyakov, A.A. Eliseev, D.I. Petukhov, A.V. Lukashin, S.-F. Chen, C.-P. Liu, G.A. Tsirlina // Electrochimica Acta. – 2011. – V.56(5). – P.2378-2384.

32. Napolskii K.S. Templating of electrodeposited platinum group metals as a tool to control catalytic activity / K.S. Napolskii, P.J. Barczuk, S.Yu. Vassiliev, A.G. Veresov, G.A. Tsirlina, P.J. Kulesza // Electrochimica Acta. – 2007. V.52(28). – P.7910-7919.

33. Prieto A.L. The electrodeposition of high-density, ordered arrays of Bi_1-xSb_x nanowires / A.L. Prieto, M. Martin-Gonzalez, J. Keyani, R. Gronsky, T. Sands, A.M. Stacy // Journal of the American Chemical Society. – 2003. - V.125(9). – P.2388-2389.

34. Borissov D. Fabrication of Iron Nanowire Arrays by Electrodeposition into Porous Alumina / D. Borissov, S. Isik-Uppenkamp, M. Rohwerder // The Journal of Physical Chemistry C. – 2009. – V.113(8). P.3133-3138.

35. Choi J. Hexagonally Arranged Monodisperse Silver Nanowires with Adjustable Diameter and High Aspect Ratio / J. Choi, G. Sauer, K. Nielsch, R. B. Wehrspohn, U. Gosele // Chemistry of materials. – 2003. -. V.15(3). – P.776-779.

36. Huang X. Orientation-Controlled Synthesis and Ferromagnetism of Single Crystalline Co Nanowire Arrays / X. Huang, L. Li, X. Luo, X. Zhu, G. Li // The Journal of Physical Chemistry C. – 2008. V.112(5). – P.1468-1472.

37. Riveros G. Crystallographically-oriented single-crystalline copper nanowire arrays electrochemically grown into nanoporous anodic alumina templates / G. Riveros, H. Gomez, A. Cortes, R.E. Marotti, E.A. Dalchiele // Applied Physics A. – 2005. – V.81(1). – P.17-24.

38. Bluhm E.A. Surface effects on cation transport across porous alumina membranes / E.A. Bluhm, E. Bauer, R.M. Chamberlin, K.D. Abney, J.S. Young, C.D. Jarvinen // Langmuir. – 1999. – V.15(25). – P.8668-8672.

39. Bluhm E.A. Surface effects on cation transport across porous alumina membranes. 2. Trivalent cations: Am, Tb, Eu, and Fe / E.A. Bluhm, E. Bauer, J.N. Fife, R.M. Chamberlin, K.D. Abney, J.S. Young, C.D. Jarvinen // Langmuir. – 2000. – V.16(17). – P.7056-7060.

40. Leprince-Wang Y. Fabrication of ZnO micro-and nano-structures by electrodeposition using nanoporous and lithography defined templates / Y. Leprince-Wang, S. Bouchaib, T. Brouri, M. Capo-Chichi, K. Laurent, J. Leopoldes, Y. Chen // Materials Science and Engineering: B. - 2010. - V.170(1-3). - P.107-112.

41. Bartlett P.N. Highly ordered macroporous gold and platinum films formed by electrochemical deposition through templates assembled from submicron diameter monodisperse polystyrene spheres / P.N. Bartlett, J.J. Baumberg, P.R. Birkin, M.A. Ghanem, M.C. Netti // Chemistry of Materials. - 2002. - V.14. -P.2199-2008.

42. Spada E.R. Homogeneous growth of antidot structures electrodeposited on Si by nanosphere lithography / E.R. Spada, A.S. Da Rocha, E.F. Jasinski, G.M.C. Pereira, L.N. Chavero, A.B. Oliveira, A. Azevedo, M.L. Santorelli // Journal of Applied Physics. - 2008. - V.103. - P.114306.

43. Valizadeh S. Electrochemical deposition of Co nanowire arrays; quantitative consideration of concentration profiles / S. Valizadeh, J.M. George, P. Leisner, L. Hultman //Electrochimica Acta. - 2001. – V.47(6). - P.865-874.

44. Schuchert I.U. Electrochemical Copper Deposition in Etched Ion Track Membranes Experimental Results and a Qualitative Kinetic Model / I.U. Schuchert, M.T. Molares, D. Dobrev, J. Vetter, R. Neumann, M. Martin // Journal of The Electrochemical Society. – 2003. – V.150(4). - P.C189-C194.

45. Newton M.R. Anisotropic diffusion in face-centered cubic opals / M.R. Newton, K.A. Morey, Y. Zhang, R.J. Snow, M. Diwekar, J. Shi, H.S. White // Nano Letters. - 2004. - V.4. - P.875-880.

46. Philippe L. Electrochemical deposition of metals inside high aspect ratio nanoelectrode array: Analytical current expression and multidimensional kinetic model for cobalt nanostructure synthesis / L. Philippe, N. Kacem, J. Michler // The Journal of Physical Chemistry C. – 2007. – V.111(13). – P.5229-5235.

47. Lopes M.C. Computational modeling of the template-assisted deposition of nanowires / M.C. Lopes, C.P. de Oliveira, E.C. Pereira // Electrochimica Acta. - 2008. – V.53(13). – P.4359-4369.

48. Ghahremaninezhad A. Diffusion-controlled growth model for electrodeposited cobalt nanowires in highly ordered aluminum oxide membrane / A. Ghahremaninezhad, A. Dolat // ECS Transactions. - 2010. – V.28(17). – P.13-25.

49. Volgin V.M. Calculation of effective diffusion coefficient in a colloidal crystal by the finite-element method / V.M. Volgin, A.D. Davydov, T.B. Kabanova // Russian Journal of Electrochemistry. - 2012. - V.48. - P.817-834.

50. Bograchev D.A. Simple model of mass transfer in template synthesis of metal ordered nanowire arrays / D.A. Bograchev, V.M. Volgin, A.D. Davydov // Electrochimica Acta. - 2013. – V.96. – P.1-7.

51. Blanco S. Modeling the Growth of Nanowire Arrays in Porous Membrane Templates / S. Blanco, R. Vargas, J. Mostany, C. Borras, B.R. Scharifker // Journal of The Electrochemical Society. - 2014. – V.161(8). – P.E3341-E3347.

52. Volgin V.M. Modeling of Through-Mask Electrochemical Micromachining / V.M. Volgin, T.B. Kabanova, A.D. Davydov // Journal of Applied Electrochemistry. - 2015. - V.45. - P.679-688.

53. Davydov A.D. Modeling of Formation of Nanostructured Metal Surfaces by Electrodeposition through a Monolayer Colloidal Crystal Mask / A.D. Davydov, T.B. Kabanova, V.M. Volgin, V.V. Lyubimov // Proc. 13th International Fischer Symposium a meeting on nanoscale electrochemistry. - 2015. - P.P09.

54. Volgin V.M. Modeling of Nanowire Array Growth during Electrodeposition of Metal into Template with Varying Porosity / V.M. Volgin, V.V. Lyubimov, D.A. Bograchev, A.D. Davydov // Proc. 13th International Fischer Symposium a meeting on nanoscale electrochemistry. - 2015. - P.P35.

55. Volgin V.M., Lyubimov V.V., Kukhar V.D., Davydov A.D. Modeling of wire electrochemical micromachining // Procedia CIRP. 2015. V.37. P.176-181.

56. Volgin V.M. Modeling of formation of nanostructured metal surfaces by electrodeposition through a monolayer colloidal crystal mask / V.M. Volgin, V.V. Lyubimov, I.V. Gnidina, A.D. Davydov // Procedia CIRP. - 2015. - V.37. - P.89-94.

57. Volgin V.M. Modeling of Electromagmetic Processes in Wire Electric Discharge Machining / V.M. Volgin, V.V. Lyubimov, V.D. Kukhar // Proc. 8th Int. Conference on Electromagnetic Processing of Materials. - 2015. - P.457-460.

58. Volgin V.M. Effect of axial magnetic field on mass transfer to cylindrical cathode under mixed convection of binary electrolyte solution / V.M. Volgin, V.V. Lyubimov, A.D. Davydov// Proc. 8th Int. Conference on Electromagnetic Processing of Materials. - 2015. - P.461-464.

59. Davydov A.D. Simulation of metal nanowire array electrodeposition into template with varying porosity / A.D. Davydov, D.A. Bograchev, T.B. Kabanova, V.M. Volgin, V.V. Lyubimov, I.V. Gnidina // Abstracts 10^th Int. Frumkin Symposium. - 2015. - P.36.

60. Volgin V.M. Simulation of electrochemical micromachining by moving tool-electrode / V.M. Volgin, V.V. Lyubimov, T.B. Kabanova, A.D. Davydov // Abstracts 10^th Int. Frumkin Symposium. – 2015. - P.92.

61. Volgin V.M. Modeling of multi-layered nanowire array growth during template electrodeposition / V.M. Volgin, V.V. Lyubimov, I.V. Gnidina, T.B. Kabanova, A.D. Davydov // Abstracts 10^th Int. Frumkin Symposium. – 2015. - P.93.

62. Volgin V.M. Modeling of numerically controlled electrochemical micromachining / V.M. Volgin, V.V. Lyubimov, A.D. Davydov // Chemical Engineering Science. - 2016. - V.140. - P.252-260.

63. Волгин В.М. Влияние аксиального магнитного поля на массоперенос к цилиндрического катоду при смешанной конвекции раствора бинарного электролита / В.М. Волгин, В.В. Любимов, А.Д. Давыдов // Cб. трудов III Региональной НТК “Высокие и критические электро- и нанотехнологии”. - 2015. - С.3-10.

64. Волгин В.М. Моделирование электроосаждения массива металлических нанопроволочек в поры матрицы с переменной пористостью / В.М. Волгин, В.В. Любимов, И.В. Гнидина, А.Д. Давыдов, Т.Б. Кабанова // Cб. трудов III Региональной НТК “Высокие и критические электро- и нанотехнологии”. - 2015. - С.11-23.

65. Волгин В.М. Моделирование формирования наноструктурированных поверхностей при электроосаждении металла через маску из монослойного коллоидного кристалла / В.М. Волгин, В.В. Любимов, И.В. Гнидина, А.Д. Давыдов, Т.Б. Кабанова // Cб. трудов III Региональной НТК “Высокие и критические электро- и нанотехнологии”. - 2015.- С.24-36.

66. Волгин В.М. Моделирование формирования микро- и наноструктурированных поверхностей при анодном растворении без использования масок / В.М. Волгин, В.В. Любимов, И.В. Гнидина, В.П. Красильников, В.Н. Татаринов // Cб. трудов III Региональной НТК “Высокие и критические электро- и нанотехнологии”. - 2015. - С.37-53.

67. Волгин В.М. Моделирование электрохимического формообразования поверхностей подвижным электродом-инструментом / В.М. Волгин, В.В. Любимов, А.Д. Давыдов // Известия ТулГУ. Технические науки. - 2015. - Вып.10. - С.54-68.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: