Главная | Обратная связь | Поможем написать вашу работу!

Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то сумма вклада с процентами вычисляется по формуле сложных процентов.

где:

S — сумма депозита с процентами,

К — сумма депозита (капитал),

P — годовая процентная ставка,

n — число периодов начисления процентов.

Пример 1. Принят депозит в сумме 100 тыс. рублей сроком на 90 дней по ставке 20 процентов годовых с начислением процентов каждые 30 дней.

(руб) – сумма банковского депозита с процентами

105013,02 – 100000 = 5 013.02 (руб) – доход

7.2. Формула сложных процентов.

Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула сложных процентов выглядит так

где:

S — сумма депозита с процентами,

К — сумма депозита (капитал),

P — процентная ставка,

n — число периодов начисления процентов.

Пример. Принят депозит в сумме 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1,5% в месяц.

Доход составил: 104567,84 – 100000 = 4567,84 (руб)

Рассмотренные выше задачи являются «кирпичиками» из которых в дальнейшем будет складываться решение нашей «экономической» задачи.

Вывод формул

Как оказалось, при решении «экономических» задач на экзамене нельзя пользоваться формулами, которые не изучаются в школе. А ведь именно эти формулы (формулы нахождения простых и сложных процентов) в значительной мере помогают при решении рассматриваемых задач.

Выведем эти формулы самостоятельно.

Для этого рассмотрим два типа задач: с начислением процентов на вклад и начислением процентов на кредит.

ЗАДАЧА 1: Вкладываем деньги в банк, открыв накопительный вклад

Положим в банк 3 млн. рублей под 15% годовых.

(В=3 млн.руб – ежегодная сумма взноса)

Вспомним, что:

Другими словами можно сказать, что сумма на нашем счёте ежегодно будет увеличиваться в 1,15 раза.

Давайте посчитаем, сколько денег будет на нашем счёте после каждого года:

В первый год, когда мы только начнём откладывать деньги, никакие проценты не накопятся, т. е. в конце года мы отложим три миллиона рублей:

В=3m (сумма взноса = 3 миллиона рублей)

В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года мы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:

3m⋅1,15+3m

Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15.

И опять же, в течение всего года мы еще отложили три миллиона рублей:

(3m⋅1,15+3m)⋅1,15+3m

Четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года мы также откладывали деньги:

((3m⋅1,15+3m)⋅1,15+3m)⋅1,15+3m

А теперь давайте раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:

((3m⋅1,15+3m)⋅1,15+3m)⋅1,15+3m = (3m⋅1,15²+3m⋅1,15+3m)⋅1,15+3m = =3m⋅1,15³+3m⋅1,15²+3m⋅1,15+3m = 3m(1,15³+1,15²+1,15+1) = =3m(1+1,15+1,15²+1,15³)

Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.

Вспомним, что если геометрическая прогрессия задана элементом b₁, а также знаменателем q, то сумма элементов будет вычисляться по формуле:

В нашем случае b ₁ = 1; q =1,15

Теперь мы можем посчитать сумму:

В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится в пять раз, т. е. составит 3m 5 = 15 миллионов.

Но нашей целью было не просто решить задачу, а увидеть закономерность, которая дала бы возможность записать формулу, позволяющую найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк.

Получили:

где:

S – общая сумма вклада

В – ежегодная сумма взноса

n – число периодов начисления процентов

ЗАДАЧА 2: Проценты по кредитам

Возьмем два миллиона рублей в кредит. При этом согласно договору мы должны платить x рублей в месяц. Допустим, что кредит мы взяли по ставке 20% годовых. Кроме того, предположим, что срок кредита составляет три года.

Давайте попробуем связать все эти величины в одну формулу.

Итак, в самом начале, как только мы вышли из банка у нас в кармане два миллиона, и это и есть наш долг.

К = 2m ( кредит = 2 миллиона рублей)

Затем спустя один год на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле: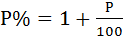

В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:

Это коэффициент суммы, которая будет начисляться в год. В конце первого года на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого нам будет необходимо оплатить оговоренную сумму, т. е. x рублей в год:

2m⋅1,2 − x

Далее к концу второго года уже на эту сумму будут вновь начислены проценты:

(2m⋅1,2 − x) ⋅1,2 − x

И вновь мы вносим платеж в размере x рублей.

Затем к концу третьего года сумма нашей задолженности еще раз увеличивается на 20%:

((2m⋅1,2 − x)⋅1,2 − x)1,2 − x

И по условию за три года мы должны полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:

((2m⋅1,2 − x)⋅1,2 − x)1,2 – x = 0

Решим это уравнение:

(2m ⋅ 1,2² − x ⋅1,2 − x) ⋅ 1,2 – x = 0

2m ⋅ 1,2³ – x ⋅ 1,2² – x ⋅ 1,2 – x = 0

2m ⋅ 1,2³= x ⋅ 1,2² + x ⋅ 1,2 + x

2m ⋅ 1,2³= x (1,2²+1,2+1)

Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:

2m ⋅ 1,2³ = x (1+1,2+1,2²)

Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Запишем:

b₁=1; q=1,2

Теперь найдем сумму геометрической прогрессии:

Следует напомнить, что сумма геометрической прогрессии с такими параметрами (b1;q) считается по формуле:

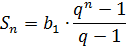
Подставляем эту формулу в наше выражение:

А теперь, запишем эту формулу в общем виде:

где:

К – сумма кредита

x – сумма платёжа

– процентная ставка

n – сроки предоставления кредита

Эта формула связывает проценты, кредиты, платежи и сроки.

Именно с помощью этой формулы и формулы суммы геометрической прогрессии решаются реальные экономические задачи из ЕГЭ по математике.

Решение задач.

Задача 1.

31 декабря 2017 года Сергей взял в банке 6 944 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Сергей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Сергей выплатил долг тремя равными платежами (т.е. за три года)?

Решение:

1 год:

2 год: =

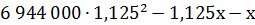
3 год:

После третьего взноса кредит погашен полностью, значит, остаток равен нулю. Решим полученное уравнение.

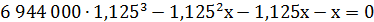
Ответ: x = 2916000 рублей.

Как видим, этот вариант записи решения не очень эффективен, так как содержит промежуточные вычисления величин. А в условиях экзамена (стрессовая ситуация) это может привести к ошибочным вычислениям и, как следствие, к неверному решению задачи.

Применим другую запись решения этой задачи.

Решение:

Пусть S = 6 944 000 – величина кредита,

x – искомая величина ежегодного платежа.

Первый год: долг: 1,125S;

платеж: x;

остаток: 1,125S – x.

Второй год: долг: 1,125(1,125S – x);

платеж: x;

остаток: 1,125(1,125S – x) – x.

Третий год: долг: 1,125(1,125(1,125S – x) – x;

платеж: x;

остаток: 0, потому что по условию было всего три платежа.

Единственное уравнение, которое надо решить:

1,125(1,125(1,125S – x) – x) – x = 0

1,125³ S = 3,390625 x

x = 2916000

Ответ: 2 916 000 рублей.

При решении этих задач можно заметить некоторую закономерность и, оформив решение в общем виде, получить выражение для описания долга по кредиту на любое количество лет.

Если S - сумма кредита,

n = , где р - процентная ставка,

х – сумма ежегодных выплат;

I год: S · k – х

II год:

III год:

IV год:

и т.д.

Воспользуемся данным выводом при решении следующей задачи.

Задача 2.

31 декабря 2017 года Родион взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на р%), затем Родион переводит очередной транш. Если он будет платить каждый год по 1 464 100 рублей, то выплатит долг за четыре года. Если по 2 674 100 рублей, то за два года. Под какой процент Родион взял деньги в банке?

Решение:

Пусть S – сумма кредита, – увеличенная процентная ставка