 |
Определение МДС реакции якоря
|
|
|
|
При определении МДС обмотки возбуждения, необходимой для создания нужного потока при нагрузке, необходимо учитывать влияние реакции якоря. Амплитуда первой гармоники МДС рeaкции якоря при токе фазы I ф
МДС реакции якоря Fa обычно разлагают на две составляющие: продольную Fd=Fa sinψ и поперечную Fq=Fa cosψ, где ψ – угол между векторами тока I ф и ЭДС холостого хода Е о. Одинаковые МДС обмотки возбуждения и якоря создают различные потоки, поэтому одну из МДС необходимо привести к другой. Так как при расчетах используют характеристику холостого хода E=f(I во), то целесообразно МДС якоря привести к МДС обмотки возбуждения. При переходе от Fd и Fq к эквивалентным Fad и Faq используют коэффициенты kad и kaq:
Коэффициенты kad и kaq, зависящие от отношений bp /τ =α и δ/τ, находят по рис. 8.1.
Рис. 8.1 Рис. 8.2
Учёт насыщения осуществляют следующим образом. Определяют коэффициенты χ q и χ d в функции отношения F δ Za /F δ (рис. 8.2), на которые умножают МДС Fad и Faq,чтобы получить их насыщенные значения F'ad и F'aq (при неравномерном зазоре δм/δ=1,5 используются 
и 
, при равномерном - 
и 
).
Для компенсации размагничивающего действия поперечной реакции якоря при насыщении магнитопровода увеличивают МДС обмотки возбуждения на некоторую величину Fqd. Например, в случае равномерного зазора
Определение параметров обмотки статора
Для установившегося режима работы
Для построения диаграмм и расчета характеристик необходимо знать параметры обмотки статора.
Активное сопротивление обмотки статора, Ом,
где ρθ – удельное сопротивление медного проводника обмотки, равное
10-6/57, 10-6/47 и 10-6/41 Ом·м соответственно при температурах 20, 75, 115 °С; q эл· n эл – сечение эффективного проводника, м2;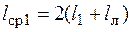 
– средняя длина витка обмотки статора, м.
|
|
|
В случае выполнения обмотки из прямоугольного провода длина лобовой части
где β= y 1/τ – относительное укорочение шага обмотки статора; Si – допустимое расстояние между соседними катушками в лобовой части; В 1 – вылет прямолинейной части катушек из паза (рис. 9.1). Параметры Si и В 1 в зависимости Рис. 9.1
от номинального напряжения определяются по табл. 9.1.
Активное сопротивление фазы в относительных единицах
где 
– базовое сопротивление.
Индуктивное сопротивление рассеяния фазы статора
где λпк, λл, λд – коэффициенты удельной (на единицу длины) магнитной проводимости пазового, лобового и дифференциального рассеяния.
Таблица 9.1
| U H, В | Si, м | B 1, м |
| ≤ 660 | 0,0035 | 0,025 |
| До 3300 | 0,005 – 0,006 | 0,035 – 0,04 |
| До 6600 | 0,006 – 0,007 | 0,04 – 0,05 |
| ≥ 10000 | 0,007 – 0,008 | 0,06 – 0,065 |
Коэффициент
где 
– проводимость между стенками паза, а 
– проводимость по коронкам зубцов. Здесь h 0, h 1, h 2 – высоты частей паза, зависящие от площади паза, занятой медью, и определяемые внешними кромками крайних проводников сторон катушек без учета изоляции (рис. 9.2); 
при 2/3≤β<1, 
– коэффициенты, зависящие от укорочения обмотки; α= bp /τ – коэффициент полюсного перекрытия; λ'к – по рис. 9.3.
Рис. 9.2 Рис. 9.3
Коэффициент проводимости лобового рассеяния
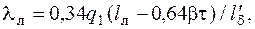
где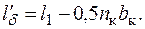 
Коэффициент проводимости дифференциального рассеяния
Индуктивное сопротивление рассеяния в относительных единицах
Индуктивное сопротивление продольной реакции якоря в относительных единицах
где 
– МДС статора при номинальном токе;
F δ0 – магнитное напряжение воздушного зазора при E=U нф; 
– коэффициент, который находят из расчета магнитной цепи для точки, соответствующей Е = 0,5 U нф.
Индуктивное сопротивление поперечной реакции якоря в относительных единицах
|
|
|
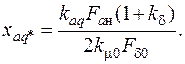
Синхронное индуктивное сопротивление по поперечной оси
Расчёт МДС обмотки возбуждения при нагрузке.
Векторная диаграмма
Для определения МДС обмотки возбуждения при нагрузке строят в относительных единицах векторную диаграмму (рис. 10.1).
Для более точного определения потока рассеяния полюсов при нагрузке необходимо иметь частичные характеристики намагничивания: 
, рис.10.2, где Ф*=Ф/Фδ, Фσ*=Фσ/Фδ, Фm*=Фm/Фδ, здесь Фδ – базовое значение потока, равное потоку при U нф; F δ za *= F δ za / F вб; Fmj *= Fmj / F вб, здесь F вб – базовое значение МДС, равное МДС обмотки возбуждения при холостом ходе и Е = U нф.
Для оценки насыщения машины следует по данным расчета маг-
Рис. 10.1 нитной цепи построить зависимость 
, рис. 10.3.
Диаграмму строят следующим образом.
10.1. В выбранном масштабе откладывают вектор номинального фазного тока 
и под углом φн к нему вектор фазного напряжения 
.
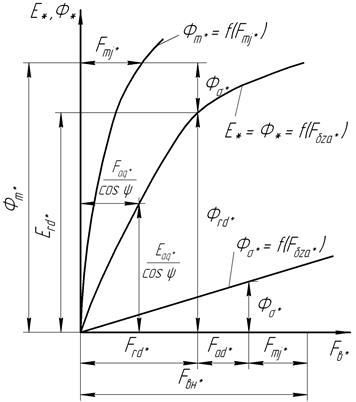
Рис. 10.2 Рис. 10.3
10.2. К вектору 
пристраивают векторы падения напряжения 
, в результате чего находят ЭДС 
, которая наводится в обмотке якоря при нагрузке. При 
векторы падения напряжения численно равны r 1* и x σ*. В крупных машинах Ir 1 относительно мало и им можно пренебречь.
10.3. По 
из зависимости 
определяют отношение 
, по которому из рис. 8.2 находят коэффициенты χ q, χ d и k.
10.4. Определяют направление вектора результирующей ЭДС по продольной оси Erd и угол ψн. Для этой цели находят относительное значение МДС
,
где 
, отложив которое по оси абсцисс характеристики 
, на оси ординат получают ЭДС, равную Еaq* /cosψ. Добавляя эту ЭДС к вектору 
, получают точку Д, через которую пройдет линия, совпадающая с направлением Ė он. Угол между током İ * и этой линией является углом ψн.
10.5. Опустив перпендикуляр из конца вектора 
на линию ОД, находят ЭДС Еrd*, наводимую в обмотке якоря результирующим потоком по продольной оси Frd* = Еrd*. Из характеристики 
по Еrd* определяют МДС Frd* (рис. 10.2).
10.6. Определяют МДС продольной реакции якоря
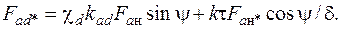
10.7. По сумме Frd* + Fad* по характеристике 
определяют поток рассеяния полюса Фσ*.
10.8. По потоку полюса Ф m *=Ф rd +Фδ* из характеристики Ф m*=f(Fmj*) определяют сумму магнитных напряжений ротора Fmj*.
10.9. Находят МДС обмотки возбуждения при нагрузке в относительных единицах
|
|
|
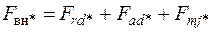
и в физических единицах (амперах) 
.
Из характеристики холостого хода 
по F вн* определяют ЭДС Е он*, которая будет наводиться в обмотке статора потоком Фн* при холостом ходе, а затем находят изменение напряжения генератора Δ U н*= E oн* -1.
|
|
|
