 |
Расчёт свободных переходных процессов САР частоты вращения ДВС по вырожденному уравнению. Расчёт свободного переходного процесса
|
|
|
|
Содержание
Введение ……………………………………………………………………….. 4
1. Математическая модель САР ДВС ……………………………………. 5
2. Определение коэффициентов дифференциального уравнения САР... 6
3. Расчет переходных процессов САР частоты вращения ДВС по вырожденному уравнению …………………………………………….. 7
4. Анализ устойчивости работы САР частоты вращения ДВС по интегралу вырожденного дифференциального уравнения ………….................... 9
5. Расчет частотных характеристик САР ДВС ………………………….. 10
6. Анализ устойчивости САР ДВС по диаграмме профессора
И. А. Вышнеградского ……………………………………………….... 12
Заключение ……………………………………………………………………. 14
Список использованных источников ………………………………………... 15
Введение
Дизельные двигатели, в отличие от бензиновых, имеют склонность к разносу, что объясняется особенностью их топливоподачи (дросселирования топлива при его отсечке в конце впрыскивания приводит к чрезмерному увеличению цикловой подачи при увеличении частоты вращения).
Автоматический регулятор защищает двигатель от разноса, однако, этим не исчерпываются его функции. Регулятор, кроме того, выполняет большое количество дополнительных функций:
- автоматическое формирование скоростной характеристики цикловой подачи топлива для облегчения пуска в условиях низких температур (зимой);
- формирование внешней скоростной характеристики с регламентированным обеспечением координат паспортных режимов двигателя;
- автоматическое изменение максимальной подачи топлива в зависимости от давления надувочного воздуха;
- автоматическое ограничение подачи топлива при значительном изменении атмосферного давления (горный корректор);
|
|
|
- ограничение подачи топлива для уменьшения содержания сажи в отработавших газах (противодымный корректор);
- и другие функции.
Математическая модель САР ДВС

Рисунок 1 – Структурная схема математической модели САР дизеля
где, η – относительная координата муфты (η=∆z/zп);
λ – относительная координата рейки насоса (λ=∆h/hп);
φ – относительная координата частоты вращения (φ=∆φР/hР);
αР - относительная координата настройки регулятора;
αН - относительная координата настройки нагрузки;
W1P=-KΨdрp- передаточная функция регулятора по настройке αP;
W2P=KРdрp – передаточная функция регулятора по регулируемой координате φ;
W3P=KDdDp – передаточная функция ДВС по координате рейки;
W4P=-KНdDp – передаточная функция двигателя по координате настройки.
Определение коэффициентов дифференциального уравнения САР
Примем значения: Iд=4 кг∙м2;
μ=3 кг.
По заданию имеем величину фактора торможения регулятора υ=7500 Н∙см;
Фактор устойчивости двигателя на разных режимах может находиться в пределах от -0,5 до -2,5 Н∙см; приму его равным - 1,5 Н∙см.
Фактор устойчивости регулятора Fp=9000 Н∙см.
Формулы для расчёта коэффициентов двигателя и регулятора:
Kp=2∙Р/Zп;
Kд≈Mн/ωд=Mн/π∙nд∙30=9,55∙Mн/nд;
их конкретные значения зависят от конкретного задания, можно лишь ориентировочно определить их порядок, но это лучше сделать в их произведении.
KpKд≈19,1∙P/zп∙Mн/nд;
Допустим: Zп=0,008 м; P=600 Н; Mн=500Н∙м; nд=2100 мин-1;
KpKд=19,1*600*500/(8∙10-3∙2100)=34,1∙104 Н2∙с;
Сравним значения коэффициентов А3, А2, А1,А0:
А3=3∙4=0,12∙102;
А2=4∙7500+3∙(-1,5)=299,95∙102;
А1=4∙9000+7500∙(-1,5)=247,5∙102;
А0=34,1∙104+9000∙(-1,5)=3275∙102 .
Сравнение этих значений показывает, что влияние коэффициента А3 не может быть значительным, поэтому уместно принять μ≈0; тогда
|
|
|
А2'=I∙ υ; А1 и А0 без изменений. Порядок уравнения САР понижается до второго и тогда оно называется вырожденным уравнением САР ДВС.
А2'∙φ+А1∙φ+А0∙φ=KдKΨαр;
При αр=0 получаем А2'∙φ+А1∙φ+А0∙φ=0;
Использование выражений позволяет получить:
1,21∙dφ/dt2+dφ/dt+13,23∙φ=0
Расчёт свободных переходных процессов САР частоты вращения ДВС по вырожденному уравнению. Расчёт свободного переходного процесса
Расчёт САР производится по уравнению:
А2'∙φ+А1∙φ+А0∙φ=0
При начальных условиях: t=0; φ=φ0; dφ/dt=0.
Изменение φ во времени после момента t=0 и является свободным переходным процессом, т.е. с помощью уравнения и упомянутых начальных условий нужно найти функцию φ=f(t).
Решение однородного дифференциального уравнения второго порядка имеет вид:
φ=C1∙eP1∙t+C2∙eP2∙t;
где, P1, P2- корни характеристического уравнения А2'∙P2+А1∙P+А0=0.
C1, C2- постоянные интегрирования (зависят от этих корней и начальных
условий).
При таком решении могут быть 2 случая:
А). P1, P2<0, тогда выражение представляет собой сумму двух
убывающих экспонент;
Б). P1, P2 =α±i∙β, тогда выражение представляет сумму косинусоиды и синусоиды.
φ=φ0∙eα∙t(cosβ∙t-α/β∙sinβ∙t)
где α=-А1/2∙А2'=-1/2∙(FP/ϑ+Fd/I); β=√А0/А2'-(А1/2∙А2')2.
Вернёмся к ранее полученному уравнению:
1,21∙dφdt2+dφdt+13,23∙φ=0
Произведём его решение:
А2'∙P2+А1∙P+А0=0
P1, P2=-0,41 ± 3,28 i
Получается второй случай, т.е. P1, P2=α±i∙β
где, α= - 0,41;
β=3,28.
Причём β является угловой частотой колебаний, выражаемой в рад/с.
Период таких колебаний вычисляется по формуле:
T=2∙π/β=2∙3,14/3,28=1,91
Весь переходный процесс описывается уравнением:
φ=φ0∙e-0,41∙t∙(cos3,28∙t+0,125∙sin3,28∙t)
Поскольку амплитудная часть синусоиды имеет пренебрежимо малое значение, всю синусоиду можно не учитывать и тогда график φ=f(t) будет выражен лишь одной затухающей косинусоидой:
φ=φ0∙e-0,41t∙(cos3,28∙t)
А в качестве начального отклонения удобно взять φ0=1 и тогда
|
|
|
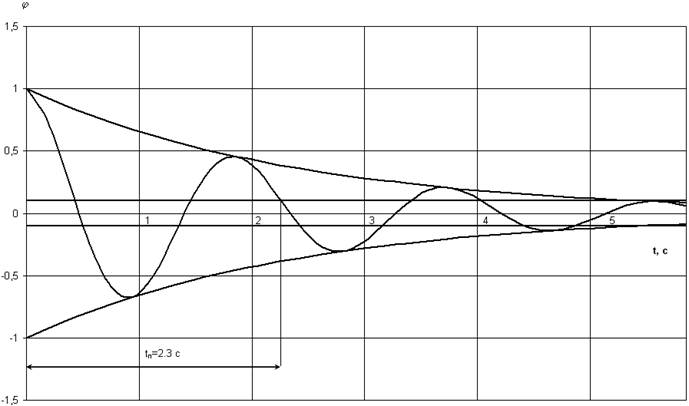
φ=e-0,41∙t∙(cos3,28∙t)
Для рисунка 2: tп- время переходного процесса, равно 9,6 с.
|
|
|


