 |
Перестановки и подстановки
|
|
|
|
Детерминанты
Пусть 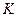 – коммутативное кольцо с единицей 1. Рассмотрим квадратную матрицу
– коммутативное кольцо с единицей 1. Рассмотрим квадратную матрицу  -го порядка
-го порядка  , каждый элемент этой матрицы
, каждый элемент этой матрицы  является элементом кольца
является элементом кольца 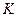 . Будем говорить, что матрица
. Будем говорить, что матрица  задана над кольцом
задана над кольцом 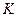 ,
, 
Детерминант (определитель) матрицы  определим следующим образом:
определим следующим образом:
 (1)
(1)
где  – определитель
– определитель  -го порядка, полученный вычеркиванием первой строки и
-го порядка, полученный вычеркиванием первой строки и  -го столбца матрицы
-го столбца матрицы  .
.  называется минором
называется минором  -го порядка матрицы
-го порядка матрицы  или дополнительным минором к элементу
или дополнительным минором к элементу  .
.
Пусть  (
( ) и
) и 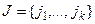 (
( ) –
) –  -элементные подмножества множества
-элементные подмножества множества  . Минором
. Минором  -ого порядка матрицы
-ого порядка матрицы  называется определитель, расположенный на пересечении строк с номерами из
называется определитель, расположенный на пересечении строк с номерами из  и столбцов с номерами из
и столбцов с номерами из 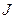 , т. е.
, т. е.  =det
=det  . Минор
. Минор  , полученный после вычеркивания из матрицы
, полученный после вычеркивания из матрицы  строк с номерами из
строк с номерами из  и столбцов с номерами из
и столбцов с номерами из 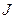 , называется дополнительным минором к минору
, называется дополнительным минором к минору  . Заметим, что
. Заметим, что  =
=  .
.
Пусть  , тогда по формуле (1) получаем, что
, тогда по формуле (1) получаем, что  .
.
Теорема 1. Пусть  (2)
(2)
 . (3)
. (3)
Тогда для любых  и
и 
 . (Формулы (2) и (3) называют разложением определителя по
. (Формулы (2) и (3) называют разложением определителя по  -му столбцу и
-му столбцу и  -ой строке соответственно).
-ой строке соответственно).
Доказательство. Докажем теорему методом математической индукции по  . Несложно проверить справедливость формул при
. Несложно проверить справедливость формул при  (сделайте это!). Далее предполагая, что формулы (2) и (3) выполнены для определителей
(сделайте это!). Далее предполагая, что формулы (2) и (3) выполнены для определителей  -го порядка, докажем их справедливость для определителей
-го порядка, докажем их справедливость для определителей  -ого порядка, где
-ого порядка, где  . Покажем сначала, что
. Покажем сначала, что 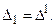
 =
=  . Разложив минор
. Разложив минор  по первой строке, получаем
по первой строке, получаем  . Тогда
. Тогда  =
=
=  =
= 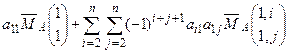 .
.
С другой стороны,  =
= 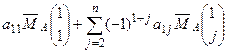 . Раскладывая минор
. Раскладывая минор  по первому столбцу, получаем
по первому столбцу, получаем 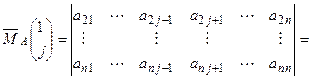
 . Значит,
. Значит,  ==
==  =
=  . Так как полученные выражения различаются только порядком суммирования, то показано, что
. Так как полученные выражения различаются только порядком суммирования, то показано, что  .
.
Прежде чем доказывать общий случай теоремы 1, дадим следующее определение.
Матрица 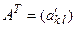 называется транспонированной к матрице
называется транспонированной к матрице  , если для любых
, если для любых  и
и  элементы этих матриц связаны соотношениями
элементы этих матриц связаны соотношениями  . Говорят также, что матрица
. Говорят также, что матрица  получается транспонированием матрицы
получается транспонированием матрицы  .
.
|
|
|
Докажем, что при транспонировании квадратной  матрицы ее определитель не меняется.
матрицы ее определитель не меняется.
Действительно, разложение  по первой строке и разложение
по первой строке и разложение  по первому столбцу совпадают.
по первому столбцу совпадают.
 , так как
, так как  при
при  .
.
Заметим теперь, что для доказательства теоремы, достаточно доказать, что  для любого
для любого  .
.
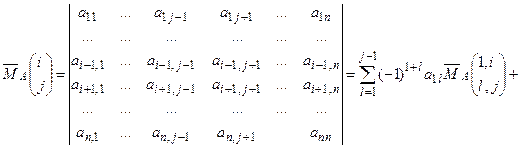
+  =
=  .
.
 =
= 
= 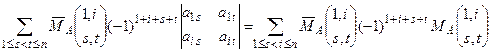 .
.
Так как 
 , получаем
, получаем 
 . Теорема доказана.
. Теорема доказана.
Пусть  и
и  , тогда произведение
, тогда произведение  называется алгебраическим дополнением минора
называется алгебраическим дополнением минора  в определителе матрицы
в определителе матрицы  , будем обозначать его как
, будем обозначать его как  .
.
Следствие 1.  . (4)
. (4)
Следствие 2. Для любого 
 =
=  . (5)
. (5)
Свойства определителя
Соотношение (4) дает нам одно из важных свойств определителя, устанавливающих равноправность строк и столбцов в определителе. Поэтому все дальнейшие свойства, устанавливаемые для строк, будут иметь место и для столбцов. Итак,
Свойство 1. При транспонировании матрицы определитель не меняется.
Свойство 2. При транспозиции (перестановке) двух строк определитель меняет знак.
Доказательство. Пусть  – матрица, полученная из матрицы
– матрица, полученная из матрицы  перестановкой первой и
перестановкой первой и  -ой строк. Согласно следствию 2 имеем, что
-ой строк. Согласно следствию 2 имеем, что  . Легко проверить, что
. Легко проверить, что  , тогда
, тогда  .
.
Итак, перестановка строк  меняет знак определителя. Перестановку
меняет знак определителя. Перестановку  -ой и
-ой и  -ой строк в определителе можно проделать за три шага:
-ой строк в определителе можно проделать за три шага:  . Свойство доказано.
. Свойство доказано.
Пусть 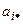 –
–  -ая строка матрицы
-ая строка матрицы  .
.
Свойство 3. Если найдется пара  и
и  такая, что
такая, что 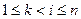 и
и  , то определитель равен нулю.
, то определитель равен нулю.
Доказательство. Пусть в матрице  найдется при некотором
найдется при некотором 
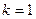 , что
, что  . Действительно, в силу (5) имеем,
. Действительно, в силу (5) имеем,  , но тогда замечая, что
, но тогда замечая, что 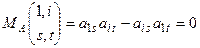 для любых
для любых 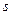 и
и 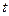 таких, что
таких, что  , получаем
, получаем  .
.
В том случае, если  , то воспользовавшись свойством 2 и поменяв местами первую и
, то воспользовавшись свойством 2 и поменяв местами первую и  -ую строки, сведем доказательство к уже разобранному случаю. Свойство доказано.
-ую строки, сведем доказательство к уже разобранному случаю. Свойство доказано.
Свойство 4. Если все элементы некоторой строки матрицы умножить на элемент  , то и сам определитель умножится на
, то и сам определитель умножится на  .
.
|
|
|
Доказательство. Пусть  – матрица, полученная из матрицы
– матрица, полученная из матрицы  умножением каждого элемента
умножением каждого элемента  -ой строки на элемент
-ой строки на элемент  , тогда
, тогда  . Действительно получаем, что
. Действительно получаем, что  . Свойство доказано.
. Свойство доказано.
Свойство 5. Если  , то
, то  , где
, где
 .
.
Доказательство. Действительно, 

 , что и требовалось доказать.
, что и требовалось доказать.
Свойство 6. Пусть  , тогда, если
, тогда, если  , то
, то  , где
, где  – матрица,
– матрица,  -ая строка которой равна
-ая строка которой равна  .
.
Доказательство провести индукцией по 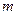 .
.
Свойство 7: Определитель не изменится, если к строке прибавить линейную комбинацию остальных строк.
Доказательство. Пусть  – матрица, полученная из матрицы
– матрица, полученная из матрицы  прибавлением к
прибавлением к  -ой строке линейной комбинации других строк. Так как
-ой строке линейной комбинации других строк. Так как  , то по свойству 5 имеем
, то по свойству 5 имеем  , где
, где  – матрица, для которой
– матрица, для которой  .
.
Применяя свойство 6, имеем, что  , где
, где  – матрица,
– матрица,  -ая строка которой есть
-ая строка которой есть  , причем
, причем 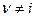 . Так как каждая из матриц
. Так как каждая из матриц  есть матрица, в которой строка
есть матрица, в которой строка  повторяется дважды, по свойству 3 получаем, что
повторяется дважды, по свойству 3 получаем, что  , значит
, значит  . Следовательно,
. Следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Перестановки и подстановки
Перестановка – это всякое расположение чисел 1,2,.., n в некотором определенном порядке. Записывать перестановку из  элементов будем в виде
элементов будем в виде  , где
, где  ,
,  .
.
Пара элементов  составляет инверсию, если
составляет инверсию, если  , а
, а  . Перестановка называется четной, если общее число инверсий
. Перестановка называется четной, если общее число инверсий  в перестановке четное, в противном случае – нечетной. Например,
в перестановке четное, в противном случае – нечетной. Например,  , значит перестановка
, значит перестановка  – нечетная.
– нечетная.
Обозначим через  вектор-столбец, такой что
вектор-столбец, такой что 
Лемма 1.  .
.
Доказательство. Применим метод индукции по  . Если
. Если  , то лемма верна. Пусть утверждение верно при
, то лемма верна. Пусть утверждение верно при  , докажем его для
, докажем его для  .
.
Так как π – перестановка, тогда существует такое  , что
, что  , т.е.
, т.е.  . Пусть
. Пусть 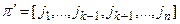 – перестановка из
– перестановка из  -ого элемента. Заметим, что
-ого элемента. Заметим, что  .
.
Действительно, раскладывая исходный определитель по  -ому столбцу, получаем, что
-ому столбцу, получаем, что 
 =
=  , что и требовалось показать.
, что и требовалось показать.
Следствие. Транспозиция меняет четность перестановки.
Доказательство. Рассмотрим сначала случай, когда символы  и
и  стоят рядом, то есть перестановка имеет вид
стоят рядом, то есть перестановка имеет вид  . Транспозиция превращает перестановку
. Транспозиция превращает перестановку 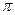 в перестановку
в перестановку  . Если в перестановке
. Если в перестановке 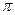 символы
символы  и
и  не составляли инверсии, то в перестановке
не составляли инверсии, то в перестановке 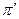 появляется новая инверсия, т.е. число инверсий увеличивается на 1. В противном случае, число инверсий уменьшится на 1. В обоих случаях четность перестановки меняется.
появляется новая инверсия, т.е. число инверсий увеличивается на 1. В противном случае, число инверсий уменьшится на 1. В обоих случаях четность перестановки меняется.
|
|
|
Пусть теперь между транспонируемыми символами  и
и  расположены
расположены 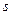 символов, т.е. перестановка имеет вид
символов, т.е. перестановка имеет вид 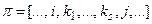 . Транспозицию символов
. Транспозицию символов  и
и  можно получить в результате последовательного выполнения
можно получить в результате последовательного выполнения  транспозиций соседних элементов сначала от
транспозиций соседних элементов сначала от  к
к  , а потом от
, а потом от  к
к  . Четность перестановки меняется нечетное число раз, значит транспозиция меняет четность перестановки, что и требовалось показать.
. Четность перестановки меняется нечетное число раз, значит транспозиция меняет четность перестановки, что и требовалось показать.
Лемма 2. Все  перестановок
перестановок  элементов можно упорядочить, начиная с любой так, чтобы переход от предыдущей к следующей осуществлялся одной транспозицией.
элементов можно упорядочить, начиная с любой так, чтобы переход от предыдущей к следующей осуществлялся одной транспозицией.
Доказательство. Применим метод индукции по числу элементов  . Для
. Для  утверждение верно. Это либо упорядочивание [1,2], [2,1], либо [2,1], [1,2].
утверждение верно. Это либо упорядочивание [1,2], [2,1], либо [2,1], [1,2].
Предположим справедливость леммы для  и докажем истинность для
и докажем истинность для  . Пусть мы должны начать с перестановки
. Пусть мы должны начать с перестановки  . Рассмотрим все перестановки из
. Рассмотрим все перестановки из  элементов, в которых на первом месте стоит
элементов, в которых на первом месте стоит  . Таких перестановок
. Таких перестановок  и их можно упорядочить согласно условию леммы по предположению индукции. Мы лишь упорядочиваем оставшуюся часть
и их можно упорядочить согласно условию леммы по предположению индукции. Мы лишь упорядочиваем оставшуюся часть  , в которой имеется
, в которой имеется  элемент. В последней из полученных таким путем перестановок совершаем транспозицию
элемент. В последней из полученных таким путем перестановок совершаем транспозицию  с другим элементом, например
с другим элементом, например  , и т.д. Таким способом можно, очевидно, перебрать все перестановки из
, и т.д. Таким способом можно, очевидно, перебрать все перестановки из  элементов. Лемма доказана.
элементов. Лемма доказана.
Следствие 1. При  число четных и нечетных перестановок одинаково и равно
число четных и нечетных перестановок одинаково и равно  .
.
Доказательство. Упорядочим все перестановки согласно лемме 2, тогда четные и нечетные будут чередоваться, так как они получены одной транспозицией, что и требовалось показать.
Подстановка – это биекция конечного множества  на себя. Подстановка записывается в виде
на себя. Подстановка записывается в виде  , где
, где  – перестановка элементов
– перестановка элементов  . Подстановка есть результат данной перестановки.
. Подстановка есть результат данной перестановки.
Отметим, что любую подстановку можно записать  различными способами, т.е.
различными способами, т.е.  .
.
Четность подстановки определяется четностью общего числа инверсий обеих перестановок, из которых она составлена, т.е. подстановка  четная, если
четная, если  – четное число.
– четное число.
Лемма 3. Четность подстановки не зависит от способа ее записи.
Доказательство. Две различные записи одной и той же подстановки получаются друг из друга перестановкой верхнего и нижнего ряда, причем на каждом этапе их четность меняется одновременно, а следовательно четность подстановки не меняется. Лемма доказана.
|
|
|
Пусть подстановка имеет вид  , где
, где  ,
, 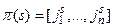 . Из перестановки
. Из перестановки  можно получить перестановку
можно получить перестановку  путем последовательного применения подстановок
путем последовательного применения подстановок  , где
, где  . Применим
. Применим  , чтобы получить
, чтобы получить  , и т.д.
, и т.д.
Таким образом,  .
.
Лемма 4. Любая подстановка раскладывается в произведение транспозиций, причем число этих сомножителей четно, когда подстановка четная.
Доказательство. Все перестановки из  символов можно получить из одной последовательным выполнением транспозиций, поэтому всякая подстановка может быть получена из данной последовательным выполнением нескольких транспозиций в нижней строке, т.е. путем последовательного умножения на подстановки вида
символов можно получить из одной последовательным выполнением транспозиций, поэтому всякая подстановка может быть получена из данной последовательным выполнением нескольких транспозиций в нижней строке, т.е. путем последовательного умножения на подстановки вида  , которые и являются транспозицией элементов
, которые и являются транспозицией элементов  и
и  . Лемма доказана.
. Лемма доказана.
Пусть  – подмножество различных элементов множества
– подмножество различных элементов множества  . Подстановка
. Подстановка  называется циклом длины
называется циклом длины 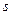 , если
, если  и
и  при
при  . Ясно, что цикл длины 2 – это транспозиция, а при
. Ясно, что цикл длины 2 – это транспозиция, а при 
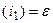 – тождественная подстановка.
– тождественная подстановка.
Доказать, что любую подстановку можно разложить в произведение независимых (т.е. непересекающихся) циклов и такое разложение единственно с точностью до перестановки сомножителей, т.е.  .
.
Всякий цикл  длины
длины 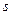 можно разложить в произведение
можно разложить в произведение  -ой транспозиции, т.е.
-ой транспозиции, т.е.  .
.
Теорема 2.  , (6)
, (6)
т.е. 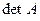 есть алгебраическая сумма
есть алгебраическая сумма  слагаемых, каждое слагаемое – произведение
слагаемых, каждое слагаемое – произведение  элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем слагаемое берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае. (Формула (6) дает разложение определителя через его элементы).
элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем слагаемое берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае. (Формула (6) дает разложение определителя через его элементы).
Доказательство. Так как  , тогда по свойству 6 линейности определителя
, тогда по свойству 6 линейности определителя  . Так как
. Так как  , если найдутся такие
, если найдутся такие 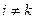 , что
, что  , получаем
, получаем  , где суммирование берется по всем перестановкам множества
, где суммирование берется по всем перестановкам множества  . В силу лемм 1 и 3 получаем
. В силу лемм 1 и 3 получаем  . Теорема доказана.
. Теорема доказана.
Следующая теорема позволяет дать аксиоматическое определение детерминанта матрицы  , основанное на полилинейной функции столбцов этой матрицы.
, основанное на полилинейной функции столбцов этой матрицы.
Теорема 3. Пусть  – функция, для которой выполняются три условия: 1)
– функция, для которой выполняются три условия: 1) 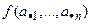 – линейна по любому столбцу
– линейна по любому столбцу  , т. е.
, т. е.
 ;
;
2) если  и
и  , то
, то  ;
;
3)  .
.
Тогда  .
.
Доказательство. Очевидно, что  . Согласно свойству 3 имеем, что если при
. Согласно свойству 3 имеем, что если при 
 , то
, то  . Далее, раскладывая каждый столбец в виде линейной комбинации единичных столбцов, получаем, что
. Далее, раскладывая каждый столбец в виде линейной комбинации единичных столбцов, получаем, что 

 . Теорема доказана.
. Теорема доказана.
Из свойств 1)-2) получаем, что при перестановке двух столбцов местами функция меняет знак. Действительно, пусть  , тогда
, тогда  , откуда получаем, что
, откуда получаем, что  .
.
|
|
|
Пусть 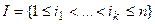 ,
, 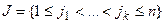 . Пусть
. Пусть  и
и  , тогда произведение
, тогда произведение  называется алгебраическим дополнением минора
называется алгебраическим дополнением минора  в определителе матрицы
в определителе матрицы  , будем обозначать его как
, будем обозначать его как  .
.
Рассмотрим функцию от столбцов матрицы 
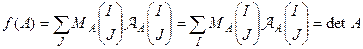 .
.
Теорема 8. (теорема Лапласа). Пусть  , тогда
, тогда  .
.
Доказательство. Пусть  .
.
1) Очевидно, что 
2) Проверим, что  линейна по каждому столбцу матрицы. Рассмотрим
линейна по каждому столбцу матрицы. Рассмотрим  -ый столбец, если
-ый столбец, если  , то
, то  линейный по этому столбцу, а если j
линейный по этому столбцу, а если j 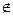 J, то
J, то  линейный по этому столбцу. Получили, что все слагаемые линейны по
линейный по этому столбцу. Получили, что все слагаемые линейны по  -ому столбцу.
-ому столбцу.
3) Пусть  и
и  . Возможны 4 случая:
. Возможны 4 случая:
1)  , тогда
, тогда  .
.
2)  , тогда
, тогда  .
.
3)  .
.
4)  .
.
Если  , тогда
, тогда  , если
, если  , тогда
, тогда  , биекция
, биекция  .
.
 .
.
Не уменьшая общности можно считать, что  -ый и
-ый и  -ый столбцы – соседние, т.е.
-ый столбцы – соседние, т.е.  , тогда
, тогда  .
.
 =
=  =
=
 , откуда
, откуда  .
.
Таким образом, рассмотренная функция столбцов  матрицы согласно теореме 3 равна
матрицы согласно теореме 3 равна 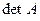 . Теорема доказана.
. Теорема доказана.
Следствие.  .
.
|
|
|


