 |
Матричная интерпретация метода Гаусса
|
|
|
|
Рассмотрим элементарные преобразования над строками матрицы 
и покажем, что каждое элементарное преобразование над строками матрицы равносильно умножению на некоторую матрицу, которую будем называть элементарной, слева.
1) Умножение 
-ой строки матрицы на число 
, т.е. 
. Элементарная матрица 
, соответствующая этому преобразованию, имеет вид:
, тогда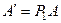 
.
2) Перестановка -ой и 
-ой строк матрицы , т.е.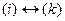 
. Элементарная матрица 
, соответствующая этому преобразованию, имеет вид:
, тогда 
.
3) Прибавление к -ой строке матрицы -ой строки, умноженной на число 
, т.е.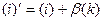 
. Элементарная матрица 
, соответствующая этому преобразованию, имеет вид:
, тогда 
.
Аналогично, любое элементарное преобразование над столбцами матрицы равносильно умножению на элементарную матрицу справа.
Элементарными преобразованиями над строками невырожденной матрицы можно привести ее к единичному виду. Пусть 
преобразованиями мы приводим матрицу к единичному виду. Эти преобразования можно заменить умножением на элементарные матрицы.
Если 
, тогда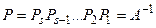 
. Получаем еще один способ нахождения обратной матрицы. Он состоит в том, что все элементарные преобразования над строками матрицы , проделаем и над матрицей 
, в итоге этих преобразований получим 
.
, так как 
, тогда 
, то есть 
.
Таким образом, элементарными преобразованиями над строками матрицы можно проверить: является ли матрица вырожденной или нет, и в том случае, если она невырожденная, то можно найти . Число операций ограничено сверху 
(
и 
циклов)
Рассмотрим способ решения систем линейных неоднородных уравнений с помощью злементарных преобразований над строками матрицы. Пусть задана система 
.
, в том случае, когда , т.е. – невырожденная, имеем , и окончательно 
, откуда 
.
|
|
|
Матричные уравнения
Матричным уравнением называется уравнение вида 
или 
, где 
– заданные матрицы. Если – невырожденная, тогда 
и 
.
Матричное уравнение вида можно решить с помощью элементарных преобразований над строками матрицы .
Матричное уравнение вида можно решить с помощью элементарных преобразований над столбцами матрицы .
Теорема 14. Определитель произведения матриц равен произведению определителей.
Доказательство. Пусть 
. Построим блочную матрицу вида 
, к первой блочной строке прибавим вторую блочную строку, умноженную на . Это преобразование равносильно умножению блочной матрицы на некоторую матрицу слева, т.е. 
. Это преобразование не меняет определителя блочной матрицы, т.е. 
. Найдем определитель каждой блочной матрицы по теореме Лапласа.
= = 
=
= 
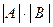, что и требовалось доказать.
Теорема 15. (Формула Бине-Коши)Пусть 
, тогда
, где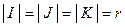 
.
Доказательство. Пусть 
(
), 
(
), 
(
).
Если 
или 
, тогда 
.
Покажем, что если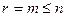 
, тогда 
и 
.
1) Если 
, то 
, так как если это не так, то 
, что противоречит первоначальному условию..
2) Пусть 
, 
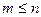. Рассмотрим матрицу 
и посчитаем ее определитель двумя способами.
1 способ. Элементарными преобразованиями, которым эквивалентно умножение справа на элементарную матрицу 
, приведем матрицу 
к виду 
. Тогда
= 
= 
= 
= 
.
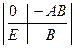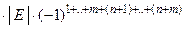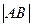
2 способ. Используятеорему Лапласа, разложим определитель матрицы по первым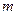 
строкам. = 
, где . Замечаем, что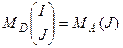 
. Пусть 
. Так как миноры, содержащие хотя бы один столбец с номером большим 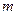равны нулю, получаем:
= 
, где 
.
Разложим 
по первым 
столбцам, тогда 
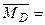
. Итак, 
.
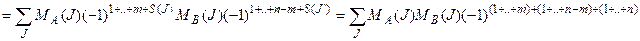Введем обозначение 
, тогда
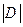
, т.к. 
= 
, получаем окончательно, что
.
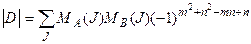Утверждение будет доказано, если числа 
и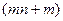 
одинаковой четности. Получаем, что число 
является четным, значит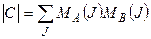 
.
Теорема 12. Ранг произведения матриц не превосходит ранга каждого из сомножителей.
|
|
|
Доказательство. Пусть 
, 
. 
, 
= 
– линейная оболочка всех столбцов .
Получаем, что система столбцов 
линейно выражается через систему столбцов , т.е.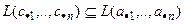 
, значит 
.
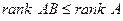Аналогично получаем, что любая строка является линейной комбинацией строк 
, тогда 
. Теорема доказана.
Матрица 
называется вырожденной (особенной, singular), если 
. Если 
, то матрица невырожденная.
Если , то не существует ни левой обратной, ни правой обратной матриц для . Так как 
(), но тогда по теореме 12 
, чего быть не может, значит уравнения 
и 
не имеют решений.
Если , то для матрицы существует обратная матрица.
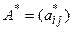- присоединенная к . 
– алгебраическое дополнение к элементу 
матрицы .
, где 
. Получили 
. Если 
, тогда 
– правая обратная матрица к .
Аналогично, 
, где 
, значит 
, тогда – левая обратная матрица к .
Замечание. Важным является то, что 
– поле, иначе делить на ∆ было бы нельзя.
[1] Габриель Крамер (1704-1752) – швейцарский математик.
|
|
|
