Зашифрование и расшифрование в IDEA.

Процесс шифрования предполагает два раунда и выходное преобразование. Один раунд состоит из преобразования входных блоков и субшифрования см рис. 17. Основой субшифрования является основной строительный блок алгоритма – мультипликативно-аддитивная (МА) структура.

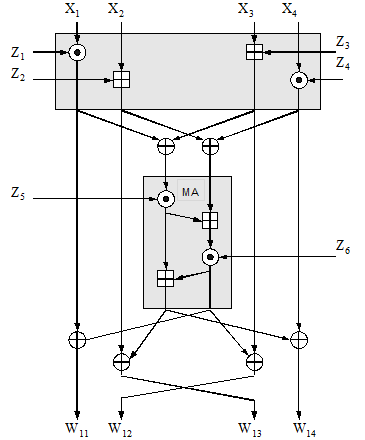
Рис.17. Раунд шифрования IDEA

Раунд начинается с преобразования, которое с помощью операции сложения и умножения связывает четыре входных подблока с четырьмя подключами. Это преобразование представлено серым прямоугольником вверху рисунка. Четыре выходных блока этого преобразования связываются операцией XOR с целью получения двух 2-битовых блоков, которые затем подаются на вход структуры МА, представленной на рисунке нижним серым прямоугольником. Кроме того, структура МА получает на входе два подключа, а в результате обработки всех полученных данных на выходе этой структуры генерируется два 2-битовых значения.

Наконец, четыре блока, полученных на выходе первого преобразования связываются с помощью операции XOR с двумя блоками, полученными на выходе структуры МА, и в результате имеется четыре выходных блока (W₁₁..W₁₄) данного раунда см. рис.18

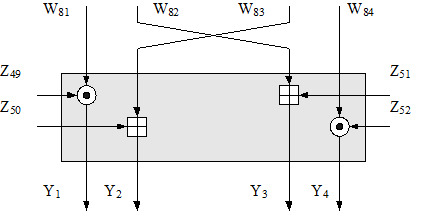
Рис.18. Выходное преобразование IDEA.

Выходное преобразование имеет структуру, подобную структуре той части предыдущего раунда шифрования, которая представлена на рисунке верхним серым прямоугольником. Единственное отличие в том, что второй и третий входные подблоки перед обработкой меняются местами. Фактически это означает отмену операции обмена, выполненной в конце второго раунда. Наличие этих лишних, по сути, перестановок обеспечивает возможность использования одной и той же структуры как для шифрования, так и для расшифрования. Кроме того, в отличие от предыдущих раундов на данной стадии используется не шесть подключей, а только четыре.

Подробно рассмотрим работу алгоритма. Выходы первого раунда расшифрования обозначим как (V₁₁..V₁₄). Промежуточные выходы первого раунда зашифрования и расшифрования обозначим соответственно как (I₁₁..I₁₄) и (J₁₁..J₁₄).

При шифровании на выходе функции выходного преобразования имеем

Y₁ = W₈₁Z₄₉, Y₂ = W₈₃ Z₅₀, Y₁ = W₈₂ Z₅₁, Y₄ = W₈₄Z₅₂.

При расшифровании на выходе первой подстадии первого раунда получаем

J₁₁ = Y₁U₁, J₁₂ = Y₂ U₂, J₁₃ = Y₃ U₃, J₁₄ = Y₄U₄.

Заменив соответствующие значения эквивалентными получим

J₁₁ = Y₁Z₄₉^-1 = W₈₁ Z₄₉Z₄₉^-1= W₈₁,

J₁₂ = Y₂ -Z₅₀ = W₈₃ Z₅₀ -Z₅₀ = W₈₃,

J₁₃ = Y₃ -Z₅₁ = W₈₂ Z₅₁ -Z₅₁ = W₈₂,

J₁₄ = Y₄Z₅₂^-1 = W₈₄ Z₅₂Z₅₂^-1= W₈₄.

Таким образом выходные значения первой подстадии первого раунда расшифрования совпадают с входными данными последней стадии шифрования за исключением того, что второй и третий блок оказываются переставленными. Следующие соотношения:

W₈₁ = I₈₁ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄),

W₈₂ = I₈₃ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄),

W₈₃ = I₈₂ÅMA_L(I₈₁ÅI₈₃, I₈₂ÅI₈₄),

W₈₄ = I₈₄ÅMA_L(I₈₁ÅI₈₃, I₈₂ÅI₈₄),

Где MA_R(X, Y) обозначает правое выходное значение структуры МА для входных значений X и Y, а MA_L(X, Y) соответственно левое выходное значение. Тогда

V₁₁ = J₁₁ÅMA_R(J₁₁ÅJ₁₃, J₁₂ÅJ₁₄) =

= W₈₁ÅMA_R(W₈₁ÅW₈₂, W₈₃ÅW₈₄) =

= I₈₁ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄) Å MA_R [I₈₁ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄) Å I₈₃ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄),

I₈₂ÅMA_L(I₈₁ÅI₈₃, I₈₂ÅI₈₄) Å I₈₄ÅMA_L(I₈₁ÅI₈₃, I₈₂ÅI₈₄)] =

= I₈₁ÅMA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄) Å MA_R(I₈₁ÅI₈₃, I₈₂ÅI₈₄) =

= I₈₁.

Точно так же получаем V₁₁ = I₈₁, V₁₂ = I₈₃, V₁₃ = I₈₂, V₁₄ = I₈₄. Таким образом, выходные данные второй подстадии процесса расшифрования совпадают с входными значениями предпоследней стадии процесса шифрования за исключением перестановки второго и третьего блоков. Далее можно показать, что соотношение сохраняется для всех последующих подстадий вплоть до V₈₁ = I₁₁, V₈₂ = I₁₃, V₈₃ = I₁₂, V₈₄ = I₁₄. Наконец входное преобразование процесса расшифрования эквивалентно преобразованию первой подстадии шифрования за исключением перестановки 2-3 блоков и результаты зашифрования/расшифрования совпадут.

Алгоритм AES (Rijndael).

Алгоритм – победитель конкурса AES, объявленный в 2000 году, был разработан двумя бельгийскими криптографами Дименом (Daemen) и Рийменом (Rijmen). Эта криптосистема не является обобщением шифра Фейстеля. В основе алгоритма – повторяющиеся раунды, каждый из которых состоит из замен, перестановок и прибавления ключа. Кроме того, AES использует сильную математическую структуру: большинство его операций основано на арифметике поля 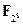. Однако в отличие от DES зашифрование и расшифрование в этом алгоритме – процедуры разные. Элементы поля 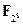хранятся в памяти компьютера в виде 8-битовых векторов (байтов). Например последовательность ‘1000 0011b’ соответствует многочлену X ⁷ + X + 1 над полем F ₂ или шестнадцатиричному числу ‘83h’.

Арифметические операции в поле 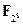соответствуют операциям над двоичными многочленами из F ₂[ X ] по модулю неприводимого многочлена

m (X) = X ⁸ + X ⁴ + X ³ + X + 1.

В алгоритме AES 32-битовые слова отождествляются с многочленами степени 3 из 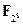[ X ]. Отождествление делается в формате «перевертыш», то есть сташий бит соответствует младшему коэффициенту многочлена. Так, например, слово

a ₀|| a ₁|| a ₂|| a ₃

соответствует многочлену

a ₃ X ³ + a ₂ X ² + a ₁ X + a ₀.

Арифметика в алгоритме совпадает с арифметическими действиями в кольце многочленов 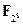[ X ] по модулю многочлена M (X) = X ⁴ + 1. Заметим, что многочлен M (X) = (X + 1)⁴ приводим, и, следовательно, арифметические действия в алгоритме отличны от операций поля, в частности, бывают пары ненулевых элементов, произведение которых равно 0.

AES – настраиваемый блочный алгоритм, который может работать с блоками из 128, 192 или 256 битов. Для каждой комбинации размера блока и размера ключа определено свое количество раундов. Здесь рассматривается самый простой вариант алгоритма, при котором блоки, как и ключ, состоят из 128 битов. В этом случае в алгоритме выполняется 10 раундов.

Алгоритм оперирует с внутренней байтовой матрицей размера 4 на 4, называемой матрицей состояний:

,

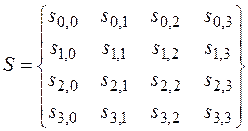которую обычно записывают как вектор 32-битовых слов. Каждое слово в векторе представляет собой столбец матрицы. Подключи также хранятся в виде матрицы 4 на 4:

.

Операции алгоритма AES.

Раундовая функция алгоритма действует с использованием четырех операций.

SubBytes. В алгоритме есть два типа S-блоков. Один применяется при зашифровании, а другой – при расшифровании. S-блоки имеют прозрачную математическую структуру. Они поочередно обрабатывают строки матрицы состояний s = [ s ₇,..., s ₀], воспринимая их как элементы поля . Их работа состоит из двух шагов.

1. Вычисляется мультипликативный обратный к элементу 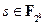и записывается как новый байт x = [ x ₇,..., x ₀]. По соглашению, элемент [0,..., 0], не имеющий обратного, остается неизменным.

2. Битовый вектор x при помощи линейного преобразования над полем F ₂ переводится в вектор y:

,

служащий выходом S-блока. Действия S-блока на стадии расшифрования состоят в обратном линейном преобразовании и вычислении мультипликативного обратного. Эти преобразования байтов можно осуществить, используя табличный поиск или микросхему, реализующую вычисление обратных элементов в 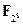и линейные преобразования.

ShiftRows. Операция осуществляет циклический сдвиг матрицы состояний. Каждая из ее строк сдвигается на свое число позиций. В рассматриваемой версии шифра это преобразование имеет вид:

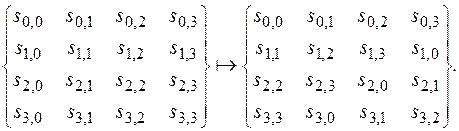
Обратная операция – тоже циклический сдвиг, но в противоположном направлении. Данная операция является рассеивающим преобразованием на протяжении нескольких раундов.

MixColumns. Операция в сочетании с предыдущей является рассеивающим преобразованием и обеспечивает зависимось каждого выходного байта от каждого входного.

Каждый столбец матрицы представляется в виде многочлена степени 3 с коэффициентами из :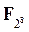

a (X) = a ₀ + a ₁ X + a ₂ X ² + a ₃ X ³.

Новый столбец получается умножением многочлена a (X) на фиксированный многочлен

с (x) = ‘02h’ + ‘01h’· X + ‘01h’· X ² + ‘03h’· X ³.

по модулю многочлена M (X) = X ⁴ + 1. Так как умножение на многочлен линейная операция, ее можно представить в виде действия матрицы:

.

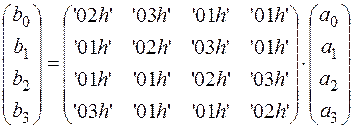Матрица коэффициентов невырождена над , поэтому операция обратима, а обратимое к ней действие реализуется матрицей, обратной к выписанной.

AddRoundKey. Сложение с подключом осуществляется побайтово по модулю 2 для каждого байта матрицы состояний с соответствующим элементом матрицы подключа. обратная операция, очевидно, совпадает с исходной.

Структура раундов.

Шифрование в алгоритме AES запишется в псевдокоде следующим образом:

AddRoundKey(S,K[0]);

For i:= 1 to 9 do Begin SubBytes(S); ShiftRows(S); MixColumns(S); AddRoundKey(S,K[i]) End;

SubBytes(S);

ShiftRows(S);

AddRoundKey(S,K[10])

Блок открытого текста, предназначенный для шифрования, записывается в виде матрицы состояний S. Полученный в результате алгоритма шифротекст представляется той же матрицей. В последнем раунде операция MixColumns не осуществляется.

Процедура расшифрования в псевдокоде:

AddRoundKey(S,K[10]);

InverseSubBytes(S);

InverseShiftRows(S);

For i:= 1 to 9 do Begin AddRoundKey(S,K[i]); InverseMixColumns(S); InverseShiftRows(S);

InverseSubBytes(S) End;

AddRoundKey(S,K[0])

Развертывание ключа.

Основной ключ алгоритма состоит из 128 битов, а нам нужно произвести 10 подключей K ₁,..., K ₁₀, каждый из которых включает в себя четыре 32-битовых слова. Здесь используется константа раунда RC_i, вычисляющаяся по правилу

RC_i = X _i (mod X ⁸ + X ⁴ + X ³ + X + 1).

Обозначим i -ый подключ через (W _{4 i} , W _{4 i+ 1}, W _{4 i+ 2}, W _{4 i+ 3},). Основной ключ алгоритма делится на четыре 32-битовых слова (k0, k1, k2, k3), после чего подключи получаются в результате выполнения прведенного ниже алгоритма. В нем через RotBytes обозначена процедура циклического сдвига слова влево на 1 байт, а через SubBytes – применение S-блока из этапа шифрования к каждому байту слова.

W[0]:=K[0]; W[1]:=K[1]; W[2]:=K[2]; W[3]:=K[3];

For i:=1 to 10 do Begin T:=RotBytes(W[4*i-1]); T:=SubBytes(T); T:=TÙRC[i];

W[4*i]:=W[4*i-4] ÙT;

W[4*i+1]:=W[4*i-3] Ù W[4*i];

W[4*i+2]:=W[4*i-2] Ù W[4*i+1];

W[4*i+3]:=W[4*i-1] Ù W[4*i+2]; End

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: