 |
Функция Эйлера. Поле. Теоремы Эйлера - Лагранжа и Ферма.
|
|
|
|
Одна из центральных задач арифметики остатков - решение сравнения:
a · x º b (mod n)
- Если НОД (a, n) = 1, то существует ровно одно решение, и оно находится с помощью a -1: так как
a · a -1 º 1 (mod n),
то, домножив обе части сравнения на a -1, получим
x º b · a -1 (mod n).
- Если НОД (a, n) = g ¹ 1 и g | b, то сравнение имеет g решений. Чтобы их найти нужно разделить исходное сравнение на g:
a’ · x’ º b’ (mod n’),
где a’ = a / g, b’ = b / g, n’ = n / g. Если x’ – решение полученного сравнения, то решение исходного сравнения - любое число вида
x = x’ + i · n’,
где i = 0, 1,..., g – 1.
- В других случаях решений нет.
Пример:
7 · x º 3 (mod 143) – одно решение,
11 · x º 3 (mod 143) – решений нет,
11 · x º 22 (mod 143) – 11 решений.
Ситуация с единственным решением наиболее интересна для криптологии, поэтому важно знать количество элементов кольца, взаимно простых с его модулем. Оно дается функцией Эйлера j и равно j (n). Значение j (n) можно легко найти по разложению числа n на простые множители. Если
,
где pi – различные простые числа, то
Функция Эйлера для любого n > 2 имеет четное значение.
- наибольшее подмножество элементов, образующих группу по умножению # = j (n). (количество элементов мультипликативной группы кольца вычетов по модулю n равно j (n)).
Особый интерес представляют частные случаи:
1. Если p простое, то j (p) = p – 1.
2. Если p и q – простые и p ¹ q, то j (p · q) = (p – 1)(q – 1).
Если p - простое число, то любой элемент в Z p (или Z / p Z) обладает мультипликативным обратным. Кольца с такими свойствами называются полями.
Определение. Полем называется множество (F, ·, +) с двумя операциями, обладающее свойствами:
- (F, +) – абелева группа с нейтральным элементом 0,
- (F \ {0}, ·) – абелева группа с нейтральным элементом 1,
|
|
|
- (F, ·, +) удовлетворяет закону дистрибутивности (умножение дистрибутивно относительно сложения).
Поле – коммутативное кольцо, в котором каждый ненулевой элемент обратим. Каждый ненулевой элемент кольца Z p взаимно прост с p, так как p простое и, следовательно, обратим. Значит Z p – конечное поле, которое обычно называют полем вычетов по модулю p и обозначают F p = {0, 1,..., p – 1}. Мультипликативная группа 
= {1,..., p – 1} поля вычетов содержит все ненулевые элементы F p.
Теорема Лагранжа.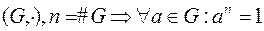 
.
Обобщение Эйлера для малой теоремы Ферма. 
, при НОД(x, n) = 1.
Малая теорема Ферма. 
.
Конечные поля.
Целые числа по простому модулю – не единственный пример конечных полей. Более общий тип полей используется при рассмотрении таких криптосистем как AES, поточных шифров на основе РСЛОС и криптосистем, на основе эллиптических кривых.
Рассмотрим множество многочленов от переменной x с коэффициентами из F p. Это множество обозначается через F p [ x ] и образует кольцо относительно естественных операций суммы и умножения многочленов. Особый интерес представляет случай p = 2.
Пример. В кольце F 2[ x ] выполнены равенства:
Зафиксируем многочлен f (x) и будем рассматривать остальные элементы кольца F p [ x ] по модулю f (x). Как и натуральные числа по модулю n, возможные остатки от деления на многочлен f (x), будут образовывать кольцо. Оно обозначается через F p [ x ]/ f (x) F p [ x ] (по аналогии с Z / n Z).
Пример. f (x) = x 4 + 1 и p = 2. Тогда
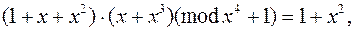
так как
По аналогии с целыми числами по модулю n, где рассматривалось сравнение
a · x º b (mod n)
можно поставить аналогичный вопрос и для многочленов. Пусть a, b и f – многочлены из F p [ x ]. Существование решения уравнения
a · a º b (mod f)
также зависит от НОД (a, f) и также возможны три ситуации. Наиболее интересна ситуация, когда НОД (a, f) = 1.
Многочлен называется неприводимым, если у него нет делителей, отличных от него самого и констант. Неприводимость многочленов - то же самое, что и простота целых чисел. Кольцо F p [ x ]/ f (x) F p [ x ] является конечным полем тогда и только тогда, когда многочлен f (x) неприводим.
|
|
|
Рассмотрим два неприводимых многочлена над полем F2
и 
.
Возникают два конечных поля
F1 = F p [ x ]/ f 1(x) F p [ x ] и F2 = F p [ x ]/ f 2(x) F p [ x ],
каждое состоит из 27 двоичных многочленов (каждый имеет ровно 7 коэффициентов равных 1 или 0), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, поскольку при вычислении суммы складываются коэффициенты многочленов по модулю 2. А вот умножаются элементы этих полей по разному:
Действительно ли различны поля F1 и F2 или это только кажущееся различие?
Изоморфны ли поля F1 и F2?
Изоморфизм: отображение j: F1 ® F2, удовлетворяющее двум требованиям:
Для построения изоморфизма между F1 и F2 достаточно показать как выражается корень f 2(x) в виде многочлена от корня f 1(x).
Изоморфизм существует между любыми двумя конечными полями с одинаковым числом элементов. Все конечные поля совпадают либо с целыми числами по простому модулю, либо с многочленами по модулю неприводимого многочлена.
Теорема. Существует единственное (с точностью до изоморфизма) конечное поле с числом элементов равным степени простого числа.
Конечное поле из q = pd элементов обозначается символом F q или GF(q) (поле Галуа из q элементов).
Любое конечное поле K содержит в себе экземпляр поля целых чисел по некоторому простому модулю p, который называется простым подполем поля K. Число элементов простого подполя называется характеристикой поля и обозначается через char K. В частности char F p = p. На конечном поле характеристики p можно определить отображение Фробениуса:
Ф: F q ® F q, Ф(a) = (a p)
которое является автоморфизмом (изоморфизмом поля с самим собой). Множество элементов из F q, остающихся неподвижными при действии Ф, совпадает с его простым подполем:
{a Î F q | a p = a} = F p.
Это утверждение – обобщение малой теоремы Ферма на случай любых конечных полей.
Ненулевые элементы конечного поля составляют конечную абелеву циклическую группу 
. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, их может быть и несколько. Всегда можно найти такой элемент g Î F q, что любой ненулевой элемент a Î F q будет представляться в виде
|
|
|
a = gx
при некотором целом показателе x.
Пример. В поле из восьми многочленов
.
В нем существует 7 ненулевых элементов, а именно
1, a, a + 1, a2, a2 + 1, a2 + a, a2 + a + 1,
где a - корень многочлена x 3 + x + 1 (искусственно введенный элемент, удовлетворяющий соотношению a3 + a + 1 = 0, в котором все действия выполняются по модулю 2).
Тогда:
a1 = a,
a2 = a2,
a3 = a + 1,
a4 = a2 + a,
a5 = a2 + 1,
a6 = a2 + a + 1,
a7 = 1
и a - примитивный элемент поля 
. Целые числа по модулю p также имеют примитивный элемент, так как F p – конечное поле.
Основные алгоритмы.
Нахождение НОД не составляет проблем, если известно разложение чисел на простые множители или многочленов на неприводимые многочлены, но разложение на простые множители или неприводимые многочлены (факторизация) – очень трудоемкая операция.
|
|
|
