Шифрование методом Цезаря

При шифровании исходного текста по данному методу каждая буква заменяется на другую букву того же алфавита путем ее смещения в используемом алфавите на число позиций, равное K. При достижении конца алфавита выполняется циклический переход к его началу.

Общая формула шифра Цезаря имеет следующий вид:

 

С=P+K (mod M),

(4.1)

 

где P – номер символа открытого текста, С – соответствующий ему номер символа шифротекста, K – ключ шифрования (коэффициент сдвига), M – размер алфавита (для русского языка M = 32)

Для данного шифра замены можно задать фиксированную таблицу подстановок, содержащую соответствующие пары букв открытого текста и шифротекста.

 

Пример 4.1

Таблица подстановок для символов русского текста при ключе K =3 представлена в таблице 4.1. Данной таблице соответствует формула:

С=P+K (mod M),

(4.2)

 

Табл. 4.1. Табл. подстановок шифра Цезаря для ключа K =3

А	®	Г		Р	®	У
Б	®	Д		С	®	Ф
В	®	Е		Т	®	Х
Г	®	Ж		У	®	Ц
Д	®	З		Ф	®	Ч
Е	®	И		Х	®	Ш
Ж	®	Й		Ц	®	Щ
З	®	К		Ч	®	Ь
И	®	Л		Ш	®	Ы
Й	®	М		Щ	®	Ъ
К	®	Н		Ь	®	Э
Л	®	О		Ы	®	Ю
М	®	П		Ъ	®	Я
Н	®	Р		Э	®	А
О	®	С		Ю	®	Б
П	®	Т		Я	®	В

 

Согласно формуле (5.2) открытый текст «БАГАЖ» будет преобразован в шифротекст «ДГЖГЙ».

Дешифрование закрытого текста, зашифрованного методом Цезаря согласно (5.1), осуществляется по формуле:

 

P=C-K (mod M)

(4.3)

 

Простая моноалфавитная замена

Шифр простой моноалфавитной замены является обобщением шифра Цезаря и выполняет шифрование по следующей схеме:

,

(4.4)

 

где - ключ шифрования, P - место символа в алфавите, .

Преобразование согласно схеме (4.4) является взаимно однозначным отображением только в том случае, если a и M взаимно простые. В этом случае для дешифрования закрытого текста выполняют обратное преобразование по формуле:

,

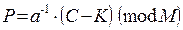(4.5)

 

Пример 4.2.

Пусть M=26, a= 3, K= 6, НОД(3,26) = 1. Тогда получаем следующую таблицу подстановок для шифра простой моноалфавитной замены.

 

 

Таблица 4.2.

A

B

C

D

E

F

G

H

I

G

K

L

M

N

O

P

Q

R

S

P

C

T

U

V

W

X

Y

Z

P

C

 

Тогда открытый текст «HOME» будет преобразован в шифротекст «BWQS».

Метод простой перестановки

При шифровании методом простой перестановки производят деление открытого текста на блоки одинаковой длины, равной длине ключа. Ключ длины n представляет собой последовательность неповторяющихся чисел от 1 до n. Символы открытого текста внутри каждого из блоков переставляют в соответствие с символами ключа внутри блока справа налево.Элемент ключа K_i в заданной позиции блока говорит о том, что на данное место будет помещен символ открытого текста с номером K_i из соответствующего блока.

 

Пример 4.3.

Зашифруем открытый текст «ПРИЕЗЖАЮДНЕМ» методом перестановки с ключом К =3142.

 

 

П	Р	И	Е	З	Ж	А	Ю	Д	Н	Е	М
И	П	Е	Р	А	З	Ю	Ж	Е	Д	М	Н

 

Для дешифрования шифротекста необходимо символы шифротекста перемещать в позицию, указанную соответствующим им символом ключа K_i слева направо.

Алгоритм Гамильтона

Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом, для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется восемь различных маршрутов. Размер ключа перестановки в данном случае равен восьми по числу вершин куба. Для примера, два из маршрутов Гамильтона представлено на рис. 4.1. Первому маршруту соответствует перестановка 4-0-2-3-1-5-7-6, второму 4-6-2-0-1-5-7-3 (нумерация символов в блоке осуществляется с нуля).

 

 

Рис. 4.1. Пример маршрутов Гамильтона

 

Пример 4.4.

Зашифруем открытый текст «ВОСЕМЬ МАРШРУТОВ» с помощью перестановок Гамильтона при использовании в качестве ключа двух перестановок, представленных на рис. 4.1.

 

В

О

С

Е

М

Ь

М

А

Р

Ш

Р

У

Т

О

В

М

В

С

Е

О

Ь

М

У

О

Ш

А

Р

Т

В

Р

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: