 |
Индивидуальные задания.
|
|
|
|
Постройте графики функций.
| 1. | y = x5+x2–10, [-10;10], 
|
| 2. | y = |tg(x)|×x, [-1;1], 
|
| 3. | y = cos(x+x5)–2, [-2;2], 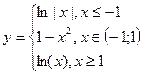
|
| 4. | y = |x3+x –10|, [-2;2], 
|
| 5. | y = ex-3, [-1;1], 
|
| 6. | y = ex·|x|, [-1;1], 
|
| 7. | y = cos(x3)–5, [-2;2], 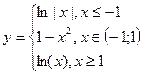
|
| 8. | y = x4-x2–х, [-5;5], 
|
| 9. | y = |x|, [-10;10], 
|
| 10. | y = |x|+5, [-10;10], 
|
| 11. | y = tg(x), [-1;1], 
|
| 12. | y = x3–2x2+5, [-10;10], 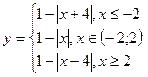
|
| 13. | y = 3cos(x)·sin(2x+3), [-10;0], 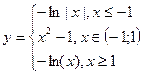
|
| 14. | y = |x2+2x-5|, [-3;3], 
|
| 15. | y = ex2-10, [-2;2], 
|
| 16. | y = x3 – 5x–15, [-2;2], 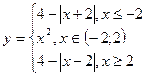
|
| 17. | y = |tg(x)|, [-1;1], 
|
| 18. | y = x3+5×|х|, [-5;5], 
|
| 19. | y = |3tg(x)×cos(x)|, [-1;1], 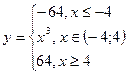
|
| 20. | y = |x2+5x-10|, [-10;5], 
|
Лабораторная работа № 10
Сортировка, фильтры и промежуточные итоги
1. В табличном процессоре создайте таблицу (рис 34).

Рис. 34. Исходные данные
2. Для столбца Дата поступления установите формат ячеек – Дата, для столбцов Цена и Стоимость – Денежный формат.
3. Отсортируйте таблицу по столбцу Наименование товара, а затем по дате поступления. Для этого:
· выделите диапазон ячеек C4:G19;
· выполните команду: вкладка ленты Данные ► панель инструментов Сортировка и фильтр ► кнопка Сортировка;
· выберите сортировать по Наименованию товара, затем добавьте новый уровень сортировки по Дате поступления (рис. 35).

Рис. 35. Сортировка
4. Переименуйте Лист 1 в Сортировка.
5. Скопируйте таблицу на Лист 2, который переименуйте в Итоги.
6. Подведем промежуточные итоги:
· выделите диапазон B4:G19;
· выполните команду: вкладка ленты Данные ► панель инструментов Структура ► кнопка  ;
;
· в появившемся диалоговом окне укажите операцию суммирования по столбцу Стоимость и нажмите кнопку ОК (рис. 36).
7. После выполнения команды подведутся промежуточные итоги (рис. 37):
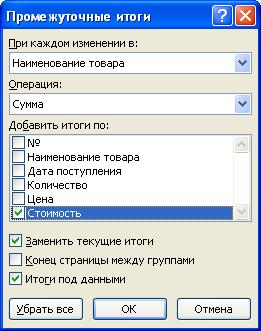
Рис. 36. Подведение итогов
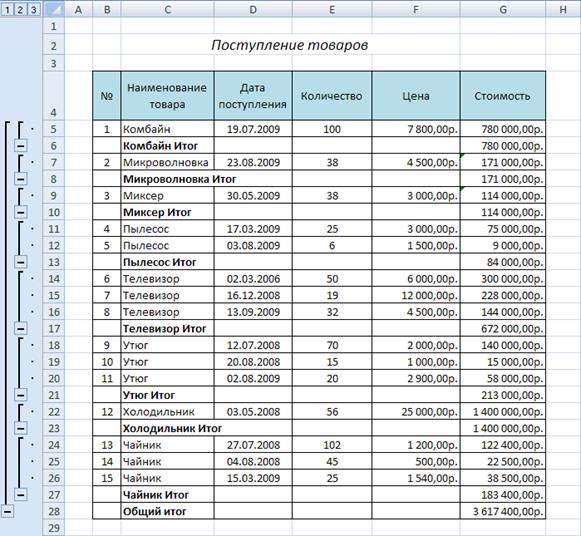
Рис. 37. Промежуточные итоги
8. Лист 3 переименуйте в Фильтр. Скопируйте на него исходную таблицу.
9. Для включения фильтра выделите диапазон данных и выполните команду: вкладка ленты Данные ► панель инструментов Сортировка и фильтр ► кнопка  .
.
|
|
|
10. После выполнения команды возле заголовков появятся кнопки фильтра  .
.
11. Отфильтруйте товары, поступившие в этом году с ценой от 3 000 до
20 000 руб.
12. Для отбора товаров, поступивших в этом году нажмите на кнопку  и в раскрывающемся списке выберите команду Фильтры по дате ► В этом году.
и в раскрывающемся списке выберите команду Фильтры по дате ► В этом году.
13. Аналогичным образом отберите товары с ценой от 3 000 до 20 000 руб.
14. После выполнения фильтров в таблице останутся следующие данные:

Рис. 38. Фильтрация данных
Лабораторная работа № 11
Сводные таблицы
Сводные таблицы применяются для группировки, обобщения и анализа данных, находящихся в списках Microsoft Excel.
1. В Microsoft Excel 2007 оформите таблицу (рис. 39).

Рис. 39. Исходные данные
2. Перейдите на Лист 2.
3. Выполните команду: вкладка ленты Вставка ► панель инструментов Таблицы ► кнопка  .
.
4. Укажите диапазон ячеек Лист1!$A$3:$C$16 и нажмите кнопку ОК.
5. Выберите поля Исполнитель и Стоимость работ (рис. 40).

Рис. 40. Список полей сводной таблицы
6. Измените заголовки в сводной таблице (рис. 41).

Рис. 41. Сводная таблица
7. На основе сводной таблицы постройте сводную диаграмму (рис. 42).

Рис. 42. Сводная диаграмма
Лабораторная работа № 12
Решение систем линейных уравнений
I Решение систем линейных уравнений методом Крамера.
Пусть задана система линейных уравнений

Неизвестные x1, x2, …, xn вычисляются по формулам:

D – определитель матрицы А,
Di – определитель матрица, полученный из матрицы А путем замены i -го столбца вектором b.
 ,
,  ,
,  ,
,  ,
,
 .
.
Пример 1. Решить систему линейных уравнений методом Крамера.
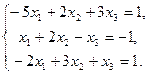
Запишем в табличном процессоре Microsoft Office Excel 2007 матрицы, которые понадобятся нам при вычислениях (рис. 43).

Рис. 43. Исходные данные
Найдем определители D, D1, D2, и D3, используя математическую функцию МОПРЕД (рис. 44).
|
|
|

Рис. 44. Вычисление определителей
Корни уравнения найдем по формулам: 
В результате всех вычислений должны получиться следующие данные:
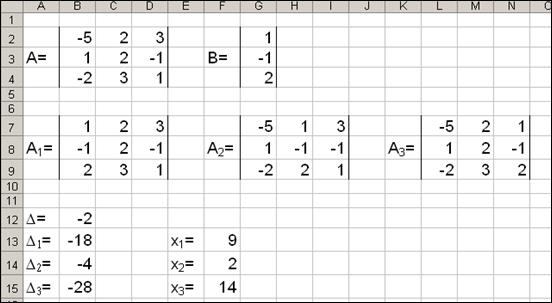
Рис. 45. Вычисление корней системы уравнений
II Решение систем линейных уравнений матричным методом
Пусть дана система линейных уравнений

Эту систему можно представить в матричном виде: А·Х=В, где
 ,
,  ,
,  .
.
Умножим систему линейных алгебраических уравнений А·Х=В слева на матрицу, обратную к А. Тогда система уравнений примет вид:
А-1·А·Х=А-1·В.
Так как А-1·А=Е (единичная матрица), то получим Е·Х=А-1·В.
Таким образом, вектор неизвестных вычисляется по формуле: Х=А-1·В.
Пример 2. Решить систему линейных уравнений матричным методом.
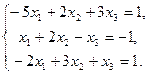
Запишем в табличном процессоре матрицу А и столбец свободных
членов В (рис. 46).

Рис. 46. Исходные данные
Нам необходимо найти обратную матрицу А-1, для этого:
1. выделите диапазон ячеек В8:D10;
2. вызовите функцию МОБР;
3. в появившемся диалоговом окне заполните поле ввода Матрица. Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица, то есть В2:D4, нажмите кнопку ОК;
4. В первой ячейке выделенного диапазона появиться некоторое число. Чтобы получить всю обратную матрицу, необходимо нажать клавишу F2, для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter (рис. 47).

Рис. 47. Обратная матрица
Осталось найти вектор неизвестных по формуле Х=А-1·В, для этого:
1. выделите диапазон ячеек G8:G10;
2. вызовите функцию МУМНОЖ;
3. в поле для первой матрицы укажите диапазон В8:D10;
4. в поле для второй матрицы укажите диапазон G2:G4;
5. нажмите кнопку ОК.
В результате должны получиться следующие значения:

Рис. 48. Вычисление корней системы уравнений
Самостоятельно сделайте проверку, для этого умножьте матрицу А на Х. В результате должен получиться столбец В.
|
|
|


