 |
Энергия, работа, мощность. Законы сохранения в механике. Поле тяготения. Движение в поле центральных сил
|
|
|
|
Вариант № 1
1. Шар массой 5 кг движется со скоростью 2 м/с и сталкивается с покоящимся шаром массой 3 кг. Вычислить работу, совершенную при деформации шаров при прямом центральном ударе. Шары считать неупругими (рис. 1).
Ответ: а) А=7,75 Дж; б) А=6,75 Дж; в) А=5,75 Дж; г) А=4,75 Дж; д) А=3,75 Дж.
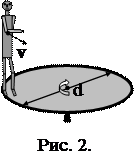
2. На горизонтальном деревянном столе лежит деревянный брусок массой 5,0 кг. В брусок попадает пуля массой 9,0 г, после чего он проходит по столу расстояние ℓ=25 см и останавливается (рис. 2). Найти скорость пули. Коэффициент трения m=0,3.
Ответ: а) v=655 м/с; б) v=665 м/с; в) v=675 м/с; г) v=685 м/с;
д) v=695 м/с.
3. Платформа в виде диска радиусом 1,5 м вращается по инерции вокруг вертикальной оси, делая 30 об/мин. В центре платформы находится человек. Определить угловую скорость платформы, если человек перейдет на ее край. Момент инерции платформы 120 кгм2 (рис. 3). Момент инерции человека рассчитывать как для материальной точки, масса человека равна 80 кг.
Ответ: а) w2=1,26 рад/с; б) w2=1,36 рад/с;
в) w2=1,46 рад/с; г) w2=1,56 рад/с; д) w2=1,66 рад/с.
4. Определить время, за которое сплошной цилиндр скатится без скольжения по наклонной плоскости (рис. 4). В начальный момент неподвижный цилиндр находится на h=60 см выше уровня нижнего конца наклонной плоскости. Потерей энергии на преодоление силы трения пренебречь. Угол наклона плоскости α=30o.
Ответ: а) t=0,86 с; б) t=0,83 с; в) t=0,80 с;
г) t=0,77 с; д) t=0,74 с.
5. В покоящийся клин массой M=2 кг попадает горизонтально летящая пуля массой m=10 г и после абсолютно упругого удара о поверхность клина отскакивает вертикально вверх (рис. 5). На какую высоту поднимется пуля, если горизонтальная скорость клина после удара оказалась равной v=1 м/с? Трением пренебречь.
|
|
|
Ответ: а) h=1,4×103 м; б) h=1,6×103 м; в) h=1,8×103 м;
г) h=2,0×103 м; д) h=2,2×103 м.
6. Найти численное значение второй космической скорости, т.е. такой скорости, которую надо сообщить телу у поверхности Земли, чтобы оно преодолело земное тяготение и навсегда удалилось от Земли.
Ответ: а) v2=12,2 км/с; б) v2=11,2 км/с; в) v2=10,2 км/с;
г) v2=9,2 км/с; д) v2=8,2 км/с.
7. Поперечная волна распространяется вдоль упругого шнура со скоростью v=15 м/с. Период колебаний точек шнура равен T=1,2 с. Определить длину волны l.
Ответ: а) l=28 м; б) l=8 м; в) l=128 м; г) l=38 м; д) l=18 м.
Вариант № 2
1. Найти работу подъема груза по наклонной плоскости, если масса груза 100 кг, длина наклонной плоскости 2 м, угол наклона 30о, коэффициент трения 0,1 и груз движется с ускорением 1 м/с2 (рис. 1).
Ответ: а) А=4,3 кДж; б) А=3,3 кДж;
в) А=2,3 кДж; г) А=1,3 кДж; д) А=0,3 кДж.
2. У ракеты стартовая масса М0=160 т, скорость истечения газов 4 км/с. После того как выгорает 90 т топлива, отбрасывается первая ступень массой 30 т. Затем выгорает еще 28 т топлива. Какова конечная скорость второй ступени ракеты?
Ответ: а) v2=7,2 км/с; б) v2=7,5 км/с; в) v2=7,8 км/с;
г) v2=8,1 км/с; д) v2=8,4 км/с.
3. Человек стоит на скамейке Жуковского и ловит рукой мяч массой m=0,4 кг, летящий в горизонтальном направлении со скоростью v=20 м/с. Траектория мяча проходит на расстоянии ℓ=0,8 м от вертикальной оси вращения скамейки (рис. 2). С какой угловой скоростью начнет вращаться скамейка с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамейки 6 кгм2.
Ответ: а) w=1,10 рад/с; б) w=1,08 рад/с;
в) w=1,06 рад/с; г) w=1,04 рад/с; д) w=1,02 рад/с.
4. Сплошной шар и обруч, скатившиеся без скольжения с 
наклонной плоскости, в конце ее имеют одинаковые линейные скорости. Определить отношение высот, с которых начали скатываться шар и обруч (рис. 3). Потерей энергии на преодоление сил трения пренебречь.
Ответ: а) h2/h1=1,43; б) h2/h1=1,53; в) h2/h1=1,63; г) h2/h1=1,73;
д) h2/h1=1,83.
|
|
|
5. Небольшое тело массой M=1 кг лежит на вершине гладкой полусферы радиусом R=1м (рис. 4). В тело попадает пуля массой m=10 г, летящая горизонтально со скоростью vo=100 м/с, и застревает в нём. Пренебрегая смещением тела во время удара, определить, на какой высоте от основания оно оторвётся от поверхности полусферы.
Ответ: а) h=0,3 м; б) h=0,4 м; в) h=0,5 м;
г) h=0,6 м; д) h=0,7 м.
6. Найти линейную скорость движения Земли по орбите, если принять, что масса Солнца равна 2×1030 кг и расстояние от Земли до Солнца равно 1,5×108 км. Орбиту Земли считать круговой.
Ответ: а) v2=31,8 км/с; б) v2=30,8 км/с; в) v2=29,8 км/с;
г) v2=28,8 км/с; д) v2=27,8 км/с.
7. Найти длину волны колебания, период которого T=10-14 с. Скорость распространения колебаний v=3×108 м/с.
Ответ: а) l=2 мкм; б) l=43 мкм; в) l=3 мкм; г) l=30 мкм;
д) l=23 мкм.
Вариант № 3
1. Вычислить работу, совершаемую на пути 12 м равномерно возрастающей силой, если в начале пути сила равна 10 Н, в конце пути 46 Н.
Ответ: а) А=356 Дж; б) А=346 Дж; в) А=336 Дж; г) А=326 Дж;
д) А=316 Дж.
2. Баллистический маятник представляет собой шар массой 3,0 кг, висящий на нити длиной 2,5 м (рис. 1). В шар попадает пуля массой 9,0 г и застревает в нем, вследствие чего система отклоняется на угол 180. Найти скорость пули.
Ответ: а) v=560 м/с; б) v=550 м/с;
в) v=540 м/с; г) v=530 м/с; д) v=520 м/с.
3. Человек стоит на скамейке Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки (рис. 2). Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамейка неподвижна, колесо вращается, делая 10 об/с. С какой угловой скоростью будет вращаться скамейка, если человек повернет стержень на угол 180о? Суммарный момент инерции скамейки и человека 6 кгм2, радиус колеса 20 см. Массу колеса в 3 кг можно считать равномерно распределенной по ободу.
Ответ: а) w2=2,3 рад/с; б) w2=2,5 рад/с;
в) w2=2,7 рад/с; г) w2=2,9 рад/с; д) w2=3,1 рад/с.
4. Сплошной шар и сплошной диск скатывается без скольжения с одинаковой высоты по наклонной плоскости. Какое тело раньше и во сколько раз достигнет конца наклонной плоскости (рис. 3)? Потерей энергии на преодоление сил трения пренебречь.
Ответ: а) t1/t2=1,00; б) t1/t2=1,08; в) t1/t2=1,12;
г) t1/t2=1,14; д) t1/t2=1,16.
5. Математический маятник длиной l=1 м и массой m=1 г отводят в горизонтальное положение и отпускают. Определить максимальное натяжение нити после удара о гвоздь, вбитый на расстоянии ℓ1=50 см от точки подвеса на линии, образующей с вертикалью угол a=60о (рис. 4).
|
|
|
Ответ: а) Tmax=2×10-2 Н; б) Tmax=3×10-2 Н;
в) Tmax=4×10-2 Н; г) Tmax=5×10-2 Н; д) Tmax=6×10-2 Н.
6. Один из спутников планеты Марс находится на расстоянии 9500 км от центра Марса. Найти период обращения спутника вокруг Марса. Масса Марса составляет 0,108 массы Земли.
Ответ: а) T=10,8 ч; б) T=9,8 ч; в) T=8,8 ч; г) T=7,8 ч; д) T=6,8 ч.
7. Звуковые колебания, имеющие частоту n=500 Гц, распространяются в воздухе. Длина волны l=70 см. Найти скорость распространения колебаний.
Ответ: а) v=450 м/с; б) v=250 м/с; в) v=550 м/с; г) v=350 м/с;
д) v=150 м/с.
Вариант № 4
1. Вагон массой 20×103 кг, движущийся равнозамедленно под действием силы трения в 6×103 Н, через некоторое время останавливается. Начальная скорость вагона 15 м/с. Найти работу сил трения и расстояние, которое пройдет он до остановки.
Ответ: а) S=385 м; б) S=375 м; в) S=365 м; г) S=355 м;
д) S=345 м.
2. Свинцовая пуля пробивает доску, при этом ее скорость падает с 400 м/с до 200 м/с. Какая часть пули расплавится? Нагреванием доски пренебречь. Начальная температура 300.
Ответ: а) Dm/m=0,59; б) Dm/m=0,69; в) Dm/m=0,79;
г) Dm/m=0,89; д) Dm/m=0,99.
3. На верхней поверхности горизонтального диска, который может вращаться вокруг вертикальной оси, проложены по окружности радиусом r=50 см рельсы игрушечной железной дороги. Масса диска 10 кг, радиус R=60 см (рис. 1). На рельсы неподвижного диска был поставлен заводной паровозик массой 1 кг и выпущен из рук. Он начал двигаться относительно рельсов со скоростью 0,8 м/с. С какой угловой скоростью будет вращаться диск?
Ответ: а) w=0,5 рад/с; б) w=0,4 рад/с;
в) w=0,3 рад/с; г) w=0,2 рад/с; д) w=0,1 рад/с.
4. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на Δℓ1=2 мм. На сколько сожмет пружину таже гиря, упавшая на конец пружины с высоты h=5 см (рис. 2)?
Ответ: а) Δℓ2=18,3 мм; б) Δℓ2=16,3 мм;
в) Δℓ2=14,3 мм; г) Δℓ2=12,3 мм; д) Δℓ2=10,3 мм.
5. Математический маятник длиной l=1 м и массой m=1 г отводят в горизонтальное положение и отпускают (рис. 3). Определить предельную высоту подъёма маятника после удара о гвоздь, вбитый на расстоянии ℓ1=50 см от точки подвеса на линии, образующей с вертикалью угол a=60о.
|
|
|
Ответ: а) hmax=0,95 м; б) hmax=0,75 м; в) hmax=0,55 м;
г) hmax=0,45 м; д) hmax=0,35 м.
6. Спутник Деймос планеты Марс находится на расстоянии 24000 км от центра Марса. Найти период обращения спутника вокруг Марса. Масса Марса составляет 0,108 массы Земли.
Ответ: а) Т=23,2 ч; б) Т=25,2 ч; в) Т=27,2 ч; г) Т=29,2 ч;
д) Т=31,2 ч.
7. Найти длину стоячей волны l, если расстояние между первой и четвертой её пучностями l=15 см.
Ответ: а) l=0,2 м; б) l=0,1 м; в) l=0,3 м; г) l=0,4 м; д) l=0,01 м.
Вариант № 5
1. Автомобиль массой 2000 кг движется в гору. Уклон горы равен 4 м на каждые 100 м пути. Коэффициент трения равен 0,08. Найти работу, совершаемую двигателем автомобиля на пути в 3 км.
Ответ: а) А=7,1×106 Дж; б) А=8,1×106 Дж; в) А=9,1×106 Дж;
г) А=10,1×106 Дж; д) А=11,1×106 Дж.
2. Тело массой 5 кг поднимают вертикально вверх на высоту h=10 м, с помощью силы 120 Н. Воспользовавшись законом сохранения энергии, найти конечную скорость тела. Начальная скорость тела равна нулю.
Ответ: а) v=13 м/с; б) v=15 м/с; в) v=17 м/с; г) v=19 м/с;
д) v=21 м/с.
3. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой 5 кг каждая. Расстояние от каждой гири до оси вращения ℓ1=70 см. Скамья вращается с частотой ν1=1 с-1. Определить частоту вращения скамьи, если человек сожмет руки так, что расстояние от каждой гири до оси вращения уменьшится до ℓ2=20 см? Момент инерции человека и скамьи относительно той же оси 2,5 кгм2 (рис. 1).
Ответ: а) n=2,75 с-1; б) n=2,65 с-1; в) n=2,55 с-1;
г) n=2,45 с-1; д) n=2,35 с-1.
4. Боек свайного молота массой 600 кг падает с некоторой высоты на сваю массой 150 кг. Найти КПД бойка, считая удар неупругим. Полезной считать энергию, пошедшую на углубление сваи.
Ответ: а) h=0,90; б) h=0,85; в) h=0,80; г) h=0,75; д) h=0,70.
5. Абсолютно упругий шар массой m=1,8 кг сталкивается с покоящимся шаром большей массы M. В результате прямого удара шар потерял 36% своей кинетической энергии. Определить массу большего шара.
Ответ: а) M=7,1 кг; б) M=6,1 кг; в) M=5,1 кг; г) M=4,1 кг;
д) M=3,1 кг.
6. Для осуществления всемирной телевизионной связи достаточно иметь три спутника Земли, вращающихся по круговой орбите в плоскости экватора с запада на восток и расположенных друг относительно друга под углом 120о. Период обращения каждого спутника 24 часа. Определить радиус орбиты и линейную скорость такого спутника.
Ответ: а) R0=52×106 м, v=4,1×103 м/с; б) R0=62×106 м, v=5,1×103 м/с; в) R0=32×106 м, v=2,1×103 м/с; г) R0=22×106 м, v=1,1×103 м/с; д) R0=42×106 м, v=3,1×103 м/с.
7. Два поезда идут навстречу друг другу. Скорость первого поезда v1=72 км/ч, скорость второго поезда v2=54 км/ч. Первый поезд подает свисток с частотой n=600 Гц. Найти частоту n' колебаний звука, который слышит пассажир второго поезда перед встречей поездов. Скорость распространения звука в воздухе c=340 м/с.
|
|
|
Ответ: а) n'=666 Гц; б) n'=766 Гц; в) n'=566 Гц; г) n'=466 Гц;
д) n'=866 Гц.
Вариант № 6
1. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа 621 Дж. Длина стержня 2 м, площадь поперечного сечения 1 мм2, модуль Юнга для алюминия Е=69 ГПа.
Ответ: а) e=9,5×102; б) e=8,5×102; в) e=7,5×102; г) e=6,5×102;
д) e=5,5×102.
2. Неподвижное тело массой m опускается плавно на массивную плиту (M>>m), движущуюся со скоростью v0=4 м/с. Сколько времени тело будет скользить по плите? Коэффициент трения m=0,2. Задачу решить, воспользовавшись законом сохранения энергии.
Ответ: а) t=1 c; б) t=2 c; в) t=3 c; г) t=4 c; д) t=5 c.
3. На скамье Жуковского стоит человек держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью 4 рад/с (рис. 1). С какой угловой скоростью будет вращаться скамья с человеком, если стержень повернуть так, чтобы он занял горизонтальное направление? Суммарный момент инерции человека и скамьи 5 кгм2. Длина стержня ℓ=1,8 м, масса 6 кг. Считать, что центр масс стержня с человеком находится на оси вращения платформы.
Ответ: а) w2=3,0 рад/с; б) w2=3,2 рад/с; в) w2=3,4 рад/с;
г) w2=3,6 рад/с; д) w2=3,8 рад/с.
4. Шар массой m1=2 кг движется со скоростью v1=4 м/с и сталкивается с покоящимся шаром массой m2=5 кг (рис. 2). Определить скорость второго шара после прямого центрального удара. Удар считать абсолютно упругим.
Ответ: а) u2=2,49 м/с; б) u2=2,39 м/с; в) u2=2,29 м/с;
г) u2=2,19 м/с; д) u2=2,09 м/с.
5. Из двух соударяющихся абсолютно упругих шаров больший шар покоится. В результате прямого удара меньший шар потерял три четверти своей кинетической энергии. Определить отношение масс шаров.
Ответ: а) M/m=2,3; б) M/m=2,4; в) M/m=2,6; г) M/m=2,8;
д) M/m=3,0.
6. На какой высоте должен вращаться искусственный спутник Земли, чтобы он находился все время над одной и той же точкой земной поверхности?
Ответ: а) h=76×106 м; б) h=66×106 м; в) h=56×106 м; г) h=46×106 м; д) h=36×106 м.
7. Два поезда идут навстречу друг другу. Скорость первого поезда v1=72 км/ч, скорость второго поезда v2=54 км/ч. Первый поезд подает свисток с частотой n=600 Гц. Найти частоту n' колебаний звука, который слышит пассажир второго поезда после встречи поездов. Скорость распространения звука в воздухе c=340 м/с.
Ответ: а) n'=142 Гц; б) n'=242 Гц; в) n'=342 Гц; г) n'=442 Гц;
д) n'=542 Гц.
Вариант № 7
1. Камень массой 200 г брошен с горизонтальной поверхности под углом к горизонту и упал на нее обратно на расстоянии S=5 м через t=1,2 с. Найти работу бросания. Сопротивлением воздуха пренебречь.
Ответ: а) А=6,2 Дж; б) А=5,2 Дж; в) А=4,2 Дж; г) А=3,2 Дж; д) А=2,2 Дж.
2. Неподвижное тело массой m опускается плавно на массивную плиту (M>>m), движущуюся со скоростью v0=4 м/с. Какое расстояние оно пройдет за время движения по плите? Коэффициент трения m=0,2. Задачу решить, воспользовавшись законом сохранения энергии.
Ответ: а) S= 5 м; б) S= 4 м; в) S= 3 м; г) S= 2 м; д) S= 1 м.
3. Платформа в виде диска диаметром d=3 м и массой M=180 кг может вращаться вокруг вертикальной оси (рис. 1). С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой m=70 кг со скоростью v=1,8 м/с относительно платформы?
Ответ: а) w=0,515 рад/с; б) w=0,525 рад/с;
в) w=0,535 рад/с; г) w=0,545 рад/с;
д) w=0,555 рад/с.
4. Абсолютно упругий шар массой 1,8 кг сталкивается с покоящимся упругим шаром большей массы (рис. 2). В результате центрального прямого удара шар потерял 36% своей кинетической энергии. Определить массу большего шара.
Ответ: а) m2=10 кг; б) m2=12 кг; в) m2=14 кг; г) m2=16 кг;
д) m2=18 кг.
5. Какую максимальную часть своей кинетической энергии может передать частица массой m1=2×10-22 г, сталкиваясь упруго с частицей массой m2=6×10-22 г, которая до столкновения покоилась?
Ответ: а) W2'/W1=0,90; б) W2'/W1=0,85; в) W2'/W1=0,80;
г) W2'/W1=0,75; д) W2'/W1=0,70.
6. Какая работа будет совершена силами гравитационного поля при падении на Землю тела массой 2 кг с высоты 1000 км?
Ответ: а) А=22×106 Дж; б) А=20×106 Дж; в) А=18×106 Дж;
г) А=16×106 Дж; д) А=14×106 Дж.
7. Найти частоту n основного тона струны, натянутой с силой F=6 кН. Длина струны l=0,8 м, ее масса m=30 г.
Ответ: а) n=250 Гц; б) n=350 Гц; в) n=450 Гц; г) n=550 Гц;
д) n=650 Гц.
Вариант № 8
1. Молот массой 1,5 т ударяет по раскаленной болванке, лежащей на наковальне, и деформирует болванку. Масса наковальни вместе с болванкой равна 20 т. Определить коэффициент полезного действия при ударе молота, считая удар неупругим. Считать работу, произведенную при деформации болванки, полезной, а работу сотрясения фундамента – бесполезной.
Ответ: а) h=0,73; б) h=0,93; в) h=0,63; г) h=0,83;
д) h=0,53.
2. На общем валу сидят маховик с моментом инерции 0,86 кг×м2 и цилиндр с радиусом 5 см, массой которого можно пренебречь. На цилиндр намотана нить, к которой подвешена гиря массой 6 кг. За какое время гиря опустится на h=1 м? Начальную скорость считать равной нулю (рис. 1).
Ответ: а) t=5,5 с; б) t=4,5 с; в) t=3,5 с; г) t=2,5 с; д) t=1,5 с.
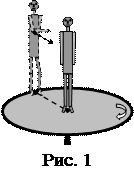
3. Платформа в виде диска может вращаться около вертикальной оси. На краю платформы стоит человек (рис. 2). На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную на платформе точку? Масса платформы 280 кг, масса человека 80 кг.
Ответ: а) j1=2020; б) j1=2040; в) j1=2060;
г) j1=2080; д) j1=2100.
4. Тележка с укрепленным на ней бруском общей массой M=1 кг стоит на горизонтальной плоскости (рис. 3). В брусок ударяет пуля, летевшая горизонтально в направлении возможного движения тележки. Пуля, пробив брусок, уменьшает свою скорость с v1=500 м/с до v2=400 м/с. Масса пули m=10 г. Какую скорость приобретает тележка с бруском?
Ответ: а) v=1,6 м/с; б) v=1,4 м/с; в) v=1,2 м/с; г) v=1,0 м/с; д) v=0,8 м/с.
5. Частица обладает импульсом p1=5×10-20 кг×м/с. Масса частицы m1=10-25 кг. Определить, какой максимальный импульс p2 может передать эта частица, сталкиваясь упруго с частицей, масса которой m2= 4×10-25 кг. Вторая частица до удара покоилась.
Ответ: а) p2=6×10-20 кг×м/с; б) p2=6,5×10-20 кг×м/с;
в) p2=7×10-20 кг×м/с; г) p2=7,5×10-20 кг×м/с; д) p2=8×10-20 кг×м/с.
6. Из бесконечности на поверхность Земли падает метеорит массой 30 кг. Определить работу, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения у поверхности Земли и ее радиус считать известными.
Ответ: а) А=1,27×109 Дж; б) А=1,47×109 Дж; в) А=1,67×109 Дж;
г) А=1,87×109 Дж; д) А=2,07×109 Дж.
7. Какую длину ℓ/ должна иметь стальная струна радиусом r=0,05 см, чтобы при силе натяжения F=0,49 кН она издавала тон с частотой n=320 Гц? Плотность стали r=7,8×103 кг/м3.
Ответ: а) ℓ'=0,15 м; б) ℓ'=0,25 м; в) ℓ'=0,35 м; г) ℓ'=0,45 м;
д) ℓ'=0,55 м.
Вариант № 9
1. На вращающейся платформе стоит человек и держит на вытянутых руках на расстоянии l1=150 см друг от друга две гири (рис. 1). Столик вращается с частотой n1=1 с-1. Человек сближает гири до расстояния l2=80 см, и частота вращения увеличивается до n2=1,5 с-1. Определить работу, произведенную человеком, если каждая гиря имеет массу m=2 кг. Момент инерции человека относительно оси платформы считать постоянным.
Ответ: а) А =42 Дж; б) А =45 Дж; в) А =48 Дж;
г) А =51 Дж; д) А =54 Дж.
2. На общем валу сидят маховик с моментом инерции 0,86 кг×м2 и цилиндр с радиусом 5 см, массой которого можно пренебречь. На цилиндр намотана нить, к которой подвешена гиря массой 6 кг. Какова будет ее конечная скорость? Начальную скорость считать равной нулю (рис. 2).
Ответ: а) v=0,28 м/с; б) v=0,38 м/с; в) v=0,48 м/с;
г) v=0,58 м/с; д) v=0,68 м/с.
3. Человек массой 60 кг находится на неподвижной платформе массой 100 кг. Какое число оборотов в минуту будет делать платформа, если человек пройдет по платформе, описывая окружность радиусом 5 м и с постоянной скоростью 4 км/ч относительно платформы (рис. 3)? Радиус платформы 10 м.
Ответ: а) n=1,4 об/мин; б) n=1,2 об/мин;
в) n=0,8 об/мин; г) n=0,6 об/мин; д) n=0,4 об/мин.
4. Тележка с укрепленным на ней бруском общей массой M=1 кг стоит на горизонтальной плоскости (рис. 4). В брусок ударяет пуля, летевшая горизонтально в направлении возможного движения тележки. Пуля, пробив брусок, уменьшает свою скорость с v1=500 м/с до v2=400 м/с. Масса пули m=10 г. Какое количество механической энергии теряет пуля?
Ответ: а) DW=410 Дж; б) DW=420 Дж; в) DW=430 Дж;
г) DW=440 Дж; д) DW=450 Дж.
5. Частица массой m1=10-24 г имеет кинетическую энергию W1=9×10-12 Дж. В результате упругого столкновения с покоящейся частицей массой m2=4×10-24 г она сообщает ей кинетическую энергию W2=5×10-12 Дж. Определить угол a, на который отклонится частица от своего первоначального направления.
Ответ: а) a=1040; б) a=1140; в) a=1240; г) a=1340; д) a=1440.
6. По круговой орбите вокруг Земли обращается спутник с периодом 90 мин. Определить высоту спутника. Ускорение свободного падения у поверхности Земли и ее радиус считать известными.
Ответ: а) h=0,22×106 м; б) h=0,32×106 м; в) h=0,42×106 м;
г) h=0,52×106 м; д) h=0,62×106 м.
7. Найти собственную частоту колебаний стальной струны, длина которой l=50 см, а диаметр – 1 мм, если натяжение струны равно 2,45×10-2 Н. Плотность стали r=7,8×103 кг/м3.
Ответ: а) n=5 с-1; б) n=4 с-1; в) n=3 с-1; г) n=2 с-1; д) n=1 с-1.
Вариант № 10
1. Шарик, диаметр которого d=6 см, катится по полу и останавливается через t=2 с, пройдя расстояние S=70 см. Определить коэффициент трения качения, считая его постоянным.
Ответ: а) k=1,3×10-3; б) k=1,4×10-3; в) k=1,5×10-3; г) k=1,6×10-3;
д) k=1,7×10-3.
2. Два груза массами m1=2 кг и m2=3 кг подвешены на нитях длиною l=2 м, так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол j=600 и выпущен (рис. 1). На какую высоту h поднимутся оба груза после удара? Удар грузов считать неупругим.
Ответ: а) h=0,38 м; б) h=0,48 м;
в) h=0,58 м; г) h=0,68 м; д) h=0,78 м.
3. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с частотой 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири (рис. 2). Какое число оборотов в минуту будет делать платформа с человеком, если человек, опустив руки, уменьшит свой момент инерции от 2,94 кгм2 до 0,98 кг×м2? Считать платформу круглым однородным диском.
Ответ: а) n2=13 об/мин; б) n2=15 об/мин;
в) n2=17 об/мин; г) n2=19 об/мин; д) n2=21 об/мин.
4. Тонкий стержень длиной ℓ=0,60 м прикреплен к горизонтальной оси, проходящей через конец стержня. Стержень отвели в сторону так, что он занял горизонтальное положение, и затем отпустили (рис. 3). Чему будет равна линейная скорость нижнего конца стержня в момент прохождения стержнем положения равновесия?
Ответ: а) v=9,2 м/с; б) v=9,0 м/с;
в) v=8,8 м/с; г) v=8,6 м/с; д) v=8,4 м/с.
5. На покоящийся шар налетает со скоростью v1=2 м/с другой шар, одинаковый с ним массы (рис. 4). В результате столкновения шар изменил направление движения на угол a=300. Определить угол b между вектором скорости второго шара и первоначальным направлением движения первого шара.
Ответ: а) b=600; б) b=500; в) b=400; г) b=300; д) b=200.
6. На какую высоту над поверхностью Земли поднимется ракета, запущенная вертикально вверх, если начальная скорость ракеты будет равна первой космической скорости?
Ответ: а) h=8,4×103 км; б) h=7,4×103 км; в) h=6,4×103 км;
г) h=5,4×103 км; д) h=4,4×103 км.
7. Найти собственную частоту колебаний воздушного столба в закрытой с обоих концов трубе, имеющей длину l=3,4 м. Скорость звука в воздухе с=340 м/с.
Ответ: а) n=10 с-1; б) n=20 с-1; в) n=30 с-1; г) n=40 с-1; д) n=50 с-1.
Вариант № 11
1. Точка совершает гармонические колебания, уравнение которых имеет вид x=5sin2pt. В момент, когда на точку действовует возвращающая сила 5×10-3 Н, точка обладает потенциальной энергией 0,1×10-3 Дж. Найти этот момент времени.
Ответ: а) t=0,06 с; б) t=0,09 с; в) t=0,12 с; г) t=0,15 с; д) t=0,18 с.
2. Тело массой 2 кг, движущееся со скоростью 3 м/с, нагоняет второе тело массой 3 кг, движущееся со скоростью 1 м/с. Каково должно быть соотношение между массами тел, чтобы при упругом ударе второе тело после взаимодействия остановилось (рис. 1)?
Ответ: а) m1/m2=5; б) m1/m2=4,5;
в) m1/m2=4; г) m1/m2=3,5; д) m1/m2=3.
3. На катере, масса которого составляет 2×105 кг, установлен водометный двигатель, выбрасывающий ежесекундно в направлении, противоположном движению катера, 200 кг воды со скоростью 5 м/с (относительно катера). Определить скорость катера через 5 мин после начала движения. Сопротивлением воды пренебречь.
Ответ: а) vk=1,7 м/с; б) vk=1,1 м/с; в) vk=1,3 м/с; г) vk=1,2 м/с; д) vk=1,5 м/с.
4. Человек стоит на скамейке Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня (рис. 2). Скамейка неподвижна, колесо вращается, делая 10 об/с. С какой угловой скоростью будет вращаться скамейка, если человек повернет стержень на угол 90о? Суммарный момент инерции скамейки и человека 6 кгм2, радиус колеса 20 см. Массу колеса в 3 кг считать равномерно распределенной по ободу.
Ответ: а) w2=1,24 рад/с; б) w2=1,34 рад/с; в) w2=1,44 рад/с;
г) w2=1,54 рад/с; д) w2=1,64 рад/с.
5. Карандаш, опирающийся заточенным концом на го 
ризонтальную плоскость, удерживается в вертикальной плоскости (рис. 3). После того, как убрали удерживающую силу, он падает на плоскость. Определить скорость, приобретенную незаточенным концом карандаша, к моменту его удара о плоскость. Карандаш рассматривать как тонкий стержень длиной ℓ=15 см. Сопротивлением воздуха пренебречь.
Ответ: а) v=2,7 м/с; б) v=2,5 м/с; в) v=2,3 м/с; г) v=2,1 м/с;
д) v=1,9 м/с.
6. Скорость, которую необходимо сообщить телу, чтобы оно покинуло гравитационное поле Земли, равна примерно 11 км/с. Если межпланетный корабль двигался при выходе из атмосферы со скоростью 12 км/с, какова будет его скорость на расстоянии 106 км от Земли?
Ответ: а) v=5,4×103 м/с; б) v=4,4×103 м/с; в) v=3,4×103 м/с;
г) v=2,4×103 м/с; д) v=1,4×103 м/с.
7. Над цилиндрическим сосудом высотой 1 м звучит камертон, имеющий собственную частоту колебаний n0=340 с-1. В сосуд медленно наливают воду. При каких положениях уровня воды в сосуде звучание камертона значительно усиливается?
Ответ: а) l0=0,25 м; l1=0,75 м; б) l0=0,35 м; l1=0,65 м;
в) l0=0,15 м; l1=0,65 м; г) l0=0,35 м; l1=0,85 м; д) l0=0,45 м; l1=0,95 м.
Вариант № 12
1. Точка совершает гармонические колебания, уравнение которых имеет вид x=5sin2pt. В момент, когда на точку действовала возвращающая сила 5×10-3 Н, точка обладает потенциальной энергией 0,1×10-3 Дж. Найти фазу колебаний.
Ответ: а) j=0,63 рад; б) j=0,73 рад; в) j=0,83 рад; г) j=0,93 рад; д) j=1,03 рад.
2. Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно ℓ=1 м. Найти скорость пули, если известно, что стержень с шаром отклонился после удара пули на угол α=10о (рис. 1).
Ответ: а) v=576 м/с; б) v=566 м/с; в) v=556 м/с; г) v=546 м/с;
д) v=536 м/с.
3. Определить скорость ракеты после выгорания полного заряда, если начальная масса ракеты 0,1 кг, масса заряда 0,09 кг, начальная скорость ракеты равна нулю, относительная скорость выхода продуктов сгорания из сопла 25 м/с. Сопротивление воздуха и ускорение силы тяжести не учитывать.
Ответ: а) v=18 м/с; б) v=28 м/с; в) v=38 м/с; г) v=48 м/с;
д) v=58 м/с.
4. Платформа в виде диска радиусом R=1,5 м и массой 180 кг вращается по инерции около вертикальной оси с частотой 10 мин-1 (рис. 2). В центре платформы стоит человек массой 60 кг. Какую линейную скорость перемещения относительно пола будет иметь человек, если он перейдет на край платформы?
Ответ: а) v=1,0 м/с; б) v=0,9 м/с; в) v=0,8 м/с; г) v=0,7 м/с;
д) v=0,6 м/с.
5. Молот массой 10 кг ударяет по небольшому куску мягкого железа, лежащему на наковальне. Масса наковальни 400 кг. Определить КПД удара молота при данных условиях. Удар считать неупругим. Полезной в данном случае является энергия, пошедшая на деформацию куска железа.
Ответ: а) h=0,95; б) h=0,96; в) h=0,98; г) h=0,94; д) h=0,97.
6. Радиус малой планеты R=100 км, средняя плотность вещества планеты r=3×103 кг/м3. Определить вторую космическую скорость у поверхности этой планеты.
Ответ: а) v=119 м/с; б) v=129 м/с; в) v=139 м/с; г) v=149 м/с;
д) v=159 м/с.
7. Реактивный самолет пролетел со скоростью 500 м/с на расстоянии 6 км от человека. На каком расстоянии от человека был самолет, когда человек услышал его звук?
Ответ: а) l=11 км; б) l=9 км; в) l=7 км; г) l=5 км; д) l=3 км.
Вариант № 13
1. Найти кинетическую энергию велосипедиста, едущего со скоростью 9 км/ч. Масса велосипедиста вместе с велосипедом 78 кг, причем суммарная масса колес велосипеда 3 кг. Колеса считать обручами.
Ответ: а) Wk=213 Дж; б) Wk=223 Дж; в) Wk=233 Дж;
г) Wk=243 Дж; д) Wk=253 Дж.
2. Пуля, летящая горизонтально, попадает в шар, подвешенный на жестком стержне массой 0,1 кг, и застревает в нем. При какой предельной длине стержня шар от удара пули сделает полный оборот вокруг оси вращения? Масса пули 5 г, масса шара 0,5 кг. Скорость пули 500 м/с. Размерами шара пренебречь.
Ответ: а) lпр=0,24 м; б) lпр=0,34 м; в) lпр=0,44 м; г) lпр=0,54 м;
д) lпр=0,64 м.
3. Две одинаковые лодки массами m=200 кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу. Скорости лодок одинаковы и равны v=1 м/с. Когда лодки поравнялись, то с первой лодки во вторую и со второй на первую одновременно перебрасывают грузы массами m1=20 кг. Определить скорости u1 и u2 лодок после перебрасывания грузов.
Ответ: а) u1=u2=0,5 м/с; б) u1=u2=0,6 м/с; в) u1=u2=0,7 м/с;
г) u1=u2=0,8 м/с; д) u1=u2=0,9 м/с.
4. Человек, стоящий на краю горизонтальной платформы, вращается по инерции вокруг неподвижной вертикальной оси с частотой 10 мин-1, переходит к ее центру (рис. 1). В результате частота вращения платформы с человеком становится равной 26 мин-1. Считая платформу круглым однородным диском, человека – точечной массой, определить массу человека. Масса платформы 100 кг
Ответ: а) m1=100 кг; б) m1=90 кг; в) m1=80 кг; г) m1=70 кг; д) m1=60 кг.
5. В баллистический маятник массой M=3 кг, висящий на нити длиной ℓ=2,5 м, попадает пуля массой m=9 г и застревает в нем, вследствие чего система отклоняется на угол α=18о (рис. 2). Найти скорость пули.
Ответ: а) v=505 м/с; б) v=515 м/с; в) v=525 м/с; г) v=535 м/с; д) v=545 м/с.
6. Две планеты обращаются вокруг Солнца по орбитам, принимаемым приближенно за круговые с радиусами R1=150×106 км (Земля) и R2=108×106 км (Венера). Найти отношение их линейных скоростей.
Ответ: а) v1/v2=0,55; б) v1/v2=0,65; в) v1/v2=0,95; г) v1/v2=0,75;
д) v1/v2=0,85.
7. Радиолокатор работает в импульсном режиме. Частота повторения импульсов n=1700 Гц, длительность импульса t=0,8 мкс. Найти максимальную дальность обнаружения цели данным радиолокатором.
Ответ: а) lmax=100 м; б) lmax=110 м; в) lmax=120 м; г) lmax=130 м; д) lmax=140 м.
Вариант № 14
1. Математический маятник длиной 24,7 см совершает затухающие колебания. Через сколько времени энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента колебаний l=0,01.
Ответ: а) Dt=121 c; б) Dt=119 c; в) Dt=117 c; г) Dt=115 c;
д) Dt=113 c.
2. Шарик из пластмассы, падая с высоты 1 м, несколько раз отскакивает от пола. Чему равен коэффициент восстановления при ударе шарика о пол, если с момента падения до второго удара о пол прошло 1,3 с? Коэффициент восстановления – отношение скорости шарика после удара к скорости до удара.
Ответ: а) k=0,90; б) k=0,92; в) k=0,94; г) k=0,96; д) k=0,98.
3. Доска массой m=10 кг свободно скользит по поверхности льда со скоростью v1 =3 м/с. На доску с берега прыгает мальчик массой 50 кг. Скорость мальчика перпендикулярна к скорости доски и равна v2=5 м/с. Определить скорость v доски с мальчиком. Силой
|
|
|
