Алгебраические действия над тензорами.

До сих пор рассмотрение векторов проводилось в некой обобщенной косоугольной системе координат. На практике обычно пользуются частным случаем прямоугольных декартовых координат e ₁^ e ₂^ e ₃. В этом случае коэффициенты a _i^k, b _kⁱ имеют смысл направляющих косинусов, и длины радиус-векторов выражаются по теореме Пифагора наиболее простым образом как сумма квадратов координат, обозначаемых как x, y, z. Отсутствие тензорных индексов у компонент вектора здесь не случайность. Дело в том, что декартова система координат привлекательна не только простотой определения длин векторов, но и совпадением взаимных базисов. Благодаря этому пропадает необходимость различать контра- и ковариатные координаты. Соответственно нет смысла говорить о верхних и нижних тензорных индексах. Иными словами, разграничение понятий ковариантного и контравариантного тензоров правомерно только в аффинной косоугольной системе координат.

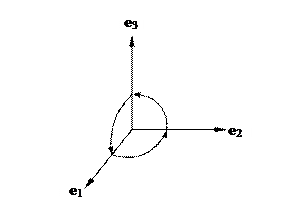
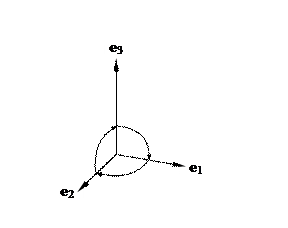
Для доказательства сказанного уточним вначале определение декартовой системы координат. Уточнения будут касаться особенностей взаимной ориентации базисных векторов. Имеются, собственно говоря, две возможности, когда они образуют правую (рис. 7а) и левую (рис. 7б) тройку.

 

Рис. 7а. Правая тройка векторов базиса.	Рис. 7б. Левая тройка векторов базиса.

 

Для правой тройки поворот вектора базиса некоторого номера до его совмещения с вектором базиса следующего (по циклической перестановке 1,2,3®2,3,1®3,1,2) номера происходит против хода часовой стрелки, т.е. подчиняется правилу правого винта. С учетом того, что векторы базиса декартовой системы представляют собой орты – единичные векторы, взаимно перпендикулярные друг другу, для них принимается:

e ₁´ e ₂= e ₃, e ₂´ e ₃= e ₁, e ₃´ e ₁= e ₂, тогда как e ₁´ e ₁= e ₂´ e ₂= e ₃´ e ₃º0. В этой связи векторное произведение некоторых двух векторов a´b представляет собой вектор c (рис. 8), перпендикулярный плоскости, в которой лежат вектора-сомножители и направленный так, чтобы поворот от вектора a к вектору b совершался против часовой стрелки, если смотреть с конца вектора c. Длина вектора c определяется при этом площадью параллелограмма, сторонами которого являются вектора-сомножители.

 

Рис. 8. Векторное произведение.	Рис. 9. Зеркальные отражения полярного (сверху) и аксиального (снизу) векторов.

 

В левой декартовой системе координат (рис. 7б) поворот любого вектора базиса до его совмещения со следующим по циклической перестановке номеров вектором базиса происходит по часовой стрелке (правило левого винта). Соответственно, направление вектора c изменится на рис. 8 на противоположное, т.е. этот вектор будет направлен вдоль штриховой прямой за плоскость. Таким образом, векторы, образующиеся в результате векторного произведения, оказываются чувствительными к выбору ориентации базисных векторов. Такие векторы называют аксиальными (т.е. осевыми) векторами или псевдовекторами. К указанному типу векторов принадлежат, например, момент силы и момент импульса, угловые скорость и ускорение. В отличие от них существуют векторы, направление которых определяется только физическим смыслом и не зависит от принимаемой правой или левой ориентации базисных векторов системы координат. Векторы этого класса (например, сила, линейная скорость и т.д.) называют полярными векторами.

Если заранее не известно, что какой-либо вектор c определяется векторным произведением некоторых других векторов, то существует простой способ для установления его принадлежность к аксиальному типу. Для этого следует воспользоваться процедурой зеркального отражения вектора (см. рис. 9.). Аксиальный вектор при зеркальном отражении не меняет своего направления. Напротив, полярный вектор вследствие такой операции меняет свое направление на противоположное.

По общему правилу используется обычно правая система декартовых координат. Пусть e ₁, e ₂, e ₃ – орты правой декартовой системы координат. Орты взаимной к ней системы координат e ¹, e ², e ³ (пока еще сохраняем для их записи контравариантную запись индексов) можно найти по формулам (4)-(6). Согласно тому, что для правой декартовой системы координат имеет место равенство e ₂´ e ₃= e ₁, формула (4) примет вид . Теперь замечая, что вследствие единичности ортов | e ₁|=1, приходим к выводу, что e ₁= e ¹. Аналогичным образом из (5) вытекает e ²= e ₂, а из (6), что e ³= e ₃. Совпадение базисов исходной и взаимной к ней декартовой системы координат можно считать доказанным.

Установленная особенность прямоугольных декартовых координат и их широкое распространение на практике не могут не затронуть вопроса о целесообразности их обобщения на случай косоугольных аффинных систем координат и значении взаимного базиса. Соответственно возникает сомнение и в практической необходимости разграничения понятий ковариантного и контравариантного тензоров. Здесь следует заметить, что даже в декартовых координатах исходный и взаимный базисы, несмотря на их совпадения, приводят к различным формам геометрических представлений. Прежде всего, если в исходном базисе координаты имеют размерность длины L, то во взаимном базисе – это обратная размерность L^-1 (обнаружить такое различие позволяет тот факт, что каждый орт взаимного базиса получается из одноименного орта исходного базиса нормировкой на квадрат модуля последнего). Поэтому исходный базис задает привычное пространство радиус-векторов, тогда как взаимный базис – пространство обратных радиус-векторов. В физике твердого тела и динамике кристаллической решетки [3] на этой основе наряду с понятием кристаллической решетки вводят понятие обратной решетки. В частности, именно на основе представления об обратной решетке в физике твердого тела формулируются фундаментальные характеристики твердого тела – зоны Бриллюэна.

Аффинная косоугольная система координат удобна в том отношении, что позволяет наиболее общим образом выразить изменения тензорных величин при преобразованиях базиса. Однако сами по себе законы преобразования тензоров (22) ничего не говорят о происходящих изменениях пространственных масштабов геометрических объектов. Для этих целей используются специальные метрические тензоры.

Рассмотрим некоторый вектор A с контра- и ковариантными компонентами Aⁱ = A×e ⁱ, A_i = A×e _i. Связи между ними можно получить, если учесть в свою очередь разложения A= A^k e _k, A= A_k e ^k:

 

, . (23)

 

Девять величин g ^ik = e ⁱ × e ^k (или g _ik = e _i × e _k) образуют тензор второго ранга, который является метрической характеристикой пространства в заданном базисе. Действительно, если рассмотреть квадрат длины дуги ds для двух бесконечно близких точек xⁱ и xⁱ + dxⁱ в исходном базисе, то будем иметь

 

. (24)

 

Точно также получим ds ²= g^ikdx_idx_k. В декартовых координатах имеем, очевидно

 

, . (25)

 

С подстановкой выражений (25), где d ^ik и d _ik – единичные тензоры, в (24) имеем, как и следовало ожидать, равенства ds ²= dxⁱdxⁱ = dx_idx_i, которые, в силу суммирования по повторяющемуся индексу, представляют теорему Пифагора.

Согласно (24) компоненты тензора g_ik определяют собой относительную долю смешанных вкладов элементарных приращений радиус-вектора по отдельным координатам в длину дуги испытываемого им результирующего перемещения. Задавая метрические свойства пространства, метрические тензоры g^ik, g_ik позволяют выражать в различных системах отсчета параметры различных геометрических элементов (длину дуги в формуле (24), элемент площади поверхности, кривизну и т.д.). Из выражений (23), например, следует, что их посредством можно осуществлять такие операции, как "подъем" и "опускание" тензорного индекса у соответствующей величины. В отношении общих свойств метрических тензоров можно также заметить, что они являются симметричными тензорами: g_ik = g_ki, g^ik = g_ik.

После того, как метрика пространства установлена, можно определить основные алгебраические операции, выполняемые над тензорами. Это сложение тензоров, умножение тензора на число, произведение тензоров, свертка или скалярное умножение тензоров. Рассмотрим их в указанной последовательности.

 

1) Сложение тензоров. Данную операцию можно производить только с тензорами одинакового вида и валентности (ранга). Подразумевается, что компоненты слагаемых тензоров имеют также одинаковую физическую размерность. Если требуется найти сумму тензоров A_ik и B_ik, то, обозначая ее как новый тензор с такими же индексами, что у слагаемых тензоров, напишем: C_ik = A_ik + B_ik. Если слагаемые тензоры есть S_ikl^pq и T_ikl^pq, имеем в качестве результата U_ikl^pq = S_ikl^pq + T_ikl^pq. Слагаемые тензоры можно брать в любой очередности. При этом фактическому сложению подвергаются компоненты тензоров с одинаковыми наборами индексов. Например, компонента U ₂₁₃¹¹ определяется равенством U ₂₁₃¹¹ = S ₂₁₃¹¹+ T ₂₁₃¹¹.

2) Умножение тензора на число. Любой тензор после умножения на число l имеет каждую компоненту, возросшую в l-раз. Ранг и тип тензора при этом не меняются. Например, при умножении тензора второго ранга R^ik на число l получаем тензор W^ik =l R^ik, матрица которого имеет вид

 

.

3) Разность тензоров можетбыть определена для тензоров одинакового вида иранга. Фактически эта операция сводится к двум первым (второй из слагаемых тензоров предварительно умножается на -1). Например, при определении разности U_ikl^pq тензоров S_ikl^pq и T_ikl^pq имеем U_ikl^pq = S_ikl^pq +(-1)× T_ikl^pq, т.е. U_ikl^pq = S_ikl^pq - T_ikl^pq.

4) Произведение тензоров. Произведением нескольких тензоров называется тензор, компоненты которого образуются произведениями компонент тензоров-сомножителей. Ранг произведения тензоров при этом равен сумме рангов тензоров-сомножителей. Например, имеем два тензора 2-го ранга A_ik и B_ik. Произведением этих тензоров будет тензор 4-го ранга C_iklm, компоненты которого имеют вид C_iklm = A_ikB_lm. Заметим, что до произведения мы могли использовать одинаковые обозначения тензорных индексов у компонент тензоров-сомножителей. Образуя же их произведение, мы вынуждены для индексов компонент второго тензора-сомножителя использовать другие обозначения (l и m вместо i и k), так как все индексы компонент возникающего тензора должны быть свободным (не повторяться). Операция произведения тензоров некоммутативна. Это означает, что при перестановке местами тензоров-сомножителей получаются неодинаковые тензоры, т.е.

.

5) Скалярное умножение или свертка тензоров. Данная операция является обобщением скалярного произведения векторов. Она выражается суммированием компонент тензора по дважды или большее число раз встречающемуся индексу. При этом повторение индекса может быть как у компонент разных тензорных величин, например, C_jrw^zt, Q_fg^vx образующих свертку – новую тензорную величину D_in^m:

(повторяющиеся индексы s – верхний, p и q – нижние, показанными жирным шрифтом), так и у подвергаемого свертке (самосвертке) единственного тензора, например T_ij^k, свертываемого по какой-либо выделенной паре индексов, скажем, i и k. В последнем случае величина

образует, очевидно, ковариантный вектор.

Выше подразумевалось, что тензоры рассматриваются в аффинной косоугольной системе координат и для каждой пары повторяющихся индексов действует правило: один из индексов – ковариантен, другой – обязательно контравариантен. Если оно не соблюдается, то образующаяся величина, вообще говоря, не является тензором. Так, свертка T _pp ^k не образует вектора. Действительно, если ее раскрыть, то имеем нумерованную величину

,

закон преобразования которой, как следует из формулы (22), имеет вид

,

явно отличающийся от закона преобразования истинного контравариантного вектора T' _pp ^k =b _j^kT _pp ^j =b _j^k (T ₁₁ ^j + T ₂₂ ^j + T ₃₃ ^j).

Свертывание можно проводить над тензорами, ранг которых не менее двух. При свертывании по двум индексам тензора ранга n образуется тензор ранга n -2. Операцию свертывания можно применять к тензору несколько раз, до тех пор, пока его ранг не станет меньше двух. По этой причине тензор четного ранга можно свернуть до скаляра, а тензор нечетного ранга, как в приведенном выше примере, – только до вектора.

Свертки по нескольким тензорам называют иногда внутренним произведением тензоров. Общим признаком тензорной свертки является понижение ранга тензора, образующегося в результате свертки по сравнению с исходным. В случае скалярного умножения или внутреннего произведения тензоров под исходным рангом подразумевается сумма рангов тензоров, входящих в свертку.

1. Свойства симметрии тензоров. Главные оси и инварианты

Тензора. Псевдотензоры.

Выше при рассмотрении метрического тензора отмечалась его симметричность. Свойство симметрии, и обратно – свойство антисимметрии, можно распространить на любые тензоры рангом не менее двух. Принято считать тензор симметричным по паре ковариантных или только контравариантных индексов i и k, если его компоненты не меняют своих значений при перестановке местами этих индексов. Математически это выразится равенствами

, (26)

которые показывают, что тензор A_ikj^m является симметричным по паре ковариантных индексов i и k. Второй тензор B_ik^lmnp симметричен уже по первой паре контравариантных индексов l и m. Что же касается тензора C_iklm^jp, то он симметричен одновременно по паре ковариантных индексов i и l, и по паре контравариантных индексов j, p.

Антисимметричность тензора подразумевает, что в результате парной перестановки однотипных индексов компоненты тензора меняют знак, т.е. вместо равенств (26) имеем

. (27)

Может показаться, что в последнем из равенств (27) пропущен знак минус в правой части. Однако все правильно, если учесть что для тензора C_iklm^jp фактически выполняются сразу две перестановки и обе перестановки относятся к антисимметрическому типу. Особенностью всякого антисимметрического тензора является равенство нулю компонент, которые соответствуют равным значениям перестановочных индексов. Действительно, если допустить обратное, то для первой такой компоненты антисимметрического тензора T_ik (i = k º1)следует написать T ₁₁=- T ₁₁. Единственная возможность выполнения этого равенства реализуется, если только T ₁₁º0.

Следствием симметричности или антисимметричности тензора является уменьшение числа его независимых компонент по сравнению с общим случаем. Если, например, общее число компонент тензора второго ранга равно 9, то, как видно из матриц (28), у симметричного тензора таких независимых компонент будет 6, а у антисимметрического – 4 (к трем ненулевым недиагональным компонентам следует добавить 0-компоненту его диагональных элементов).

 

. (28)

 

Свойства симметрии или антисимметрии тензоров не зависят от выбора системы координат. Представляется, что в общем случае отсутствие симметрии или антисимметрии тензора можно рассматривать как следствие наложения некоторых других тензоров с указанными качествами. Проще всего это положение иллюстрируется для тензоров второго ранга, допускающих единственную парную перестановку индексов. Так, мы можем написать

.

Величина очевидно удовлетворяет определению симметричного тензора S_ik, а – определению антисимметрического тензора A_ik. Таким образом, заключаем, что любой тензор можно рассматривать как сумму симметричного и антисимметрического тензоров.

Способность тензора складываться из симметричной и антисимметричной частей необходимо дополнить рецептом построения этих частей. Компоненты симметричного S_ik и антисимметрического A_ik тензоров наряду с компонентами T_ik исходного тензора содержат также компоненты тензора с переставленными индексами. Из сопоставления матриц тензоров

,

следует, что они переходят друг в друга заменой "строка«столбец". Тензоры T_ik и T_ki неодинаковы. Для того, чтобы из произвольного заданного тензора получить тензор, симметричный или антисимметрический, существуют специальные процедуры симметрирования и альтернирования. Симметрированием называется операция перестановки индексов пары с последующим сложением полученного тензора с исходным. В результате получается тензор, симметричный относительно выделенной пары индексов. Альтернирование (от англ. alternate – чередоваться) состоит уже не в сложении, а вычитании из полученного перестановкой индексов тензора исходного тензора. Итоговый тензор оказывается антисимметрическим тензором относительно выделенной пары индексов.

Антисимметрический тензор в (28) имеет только 3 независимых ненулевых компоненты и возникает соблазн сопоставить их некоторому вектору. Закон преобразования тензора A_ik задается первой из формул (22). С привлечением условия антисимметричности тензора A_lm =- A_ml ее можно привести к виду

, (29)

где индексы l и m в сумме правой стороны принимают циклические перестановки: 12, 23, 31. Переобозначая далее компоненты тензора как A ₁₂=- A ₂₁º A ₃, A ₃₁=- A ₁₃º A ₂, A ₂₃=- A ₃₂º A ₁ или сокращенно A_lm º A_n (индексы l, m и n составляют циклические перестановки), имеем аналогичное представление и в новой системе, т.е. A'_ik º A'_r, где i, k, r также составляют циклические перестановки. Формулу (29) можно, поэтому, переписать следующим образом

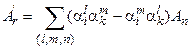. (30)

Сумма в правой стороне (30) осуществляется по циклическим перестановкам индексов, т.е. содержит только три слагаемых.

В тензорной форме разложение (12) векторов базиса e '_i новой системы координат по базису e _l старой системы координат имеет вид e '_i =α _i^l e _l. Поэтому для величин, содержащихся под знаком суммы формулы (30) в круглых скобках получим представление

. (31)

При выводе равенства (31) подразумевалось, что старая система координат была правой. Допуская, что это качество сохранится и в новой системе координат, имеем в силу цикличности перестановки в (30) индексов i, k, r: (e ' _i ´ e ' _k)= e ' _r. Формула (30) в итоге преобразуется в равенство

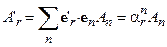. (32)

Если бы старая система координат была правой, а новая оказалась левой, то векторное произведение получалось бы со знаком минус, т.е.(e ' _i ´ e ' _k)=- e ' _r, и вместо (32) имело бы место равенство

. (33)

Выражения (32), (33) показывают, что компоненты антисимметрического тензора (обозначены как A_r) удовлетворяют закону преобразования векторных величин, т.е. действительно образуют вектор. При этом вектор меняет знак, если правая (левая) система координат меняется на левую (правую) систему координат. Такую чувствительность к взаимной ориентации базисных векторов демонстрируют аксиальные векторы или псевдовекторы. Таким образом, антисимметричному тензору второго ранга всегда можно сопоставить аксиальный вектор.

Антисимметрический тензор второго ранга можно классифицировать как псевдотензор. Естественно распространить это понятие на тензоры более высоких и более низких рангов. Подкласс псевдотензоров объединяет все величин, формулы преобразования компонент которых меняют знак при преобразованиях, переводящих правую (левую) систему координат в левую (правую).

При любых линейно-ортогональных преобразованиях координат фундаментальное свойство демонстрирует определитель D матрицы (13) коэффициентов α _i^k прямого преобразования. Именно, D=±1. Чтобы убедиться в этом учтем возможность не различать ковариантные и контравариантные индексы тензоров в случае прямоугольных систем координат, по отношению к которым только и имеет смысл понятие линейно-ортогонального преобразования. Условию же ортогональности преобразования в силу (25) можно будет придать вид тензорного равенства

, (34)

где d _ik – единичный тензор. По теореме умножения определителей [1] имеем согласно (34), что det||d _ik ||=det||α _il ||×det||α _lk || и поскольку, по определению det||α _lk ||= det||α _il ||ºD, а

,

приходим к равенству D²=1, которое и доказывает сделанное выше утверждение.

Существование двух значений инварианта[1] D=±1 объясняется нашей способностью различать в пространственном восприятии геометрических объектов "правое" и "левое". Можно показать, что значение D=1 соответствует классу непрерывных преобразований системы координат в виде сдвигов и вращений, при которых не происходит замена правой системы координат на левую или наоборот. В простейшем случае можно говорить о тождественном преобразовании x' ₁= x ₁, x' ₂= x ₂, x' ₃= x ₃, когда значение D=1 очевидно. Другим примером является преобразование x' ₁= x ₂, x' ₂=- x ₁, x' ₃= x ₃, описывающее поворот системы координат на угол p/2 вокруг оси x ₃ (см. рис. 10).

	x' 2
Рис. 10. Преобразование вращением.	Рис. 11. Преобразование отражением.

 

Второе значение инварианта D=-1 соответствует классу преобразования, связанного с зеркальным отражением – процедурой уже обсуждавшейся (рис. 9) для пояснения разницы между полярными и аксиальными векторами. В этом классе преобразования никакие две системы координат не могут совместиться друг с другом в результате только непрерывного движения. При достижении совмещения двух их одноименных осей третьи оси уложатся вдоль общей прямой, но будут иметь противоположные направления. Преобразование зеркального отражения обеспечит, как раз, взаимное обращение направлений этих третьих осей и возможность перехода из одной системы координат в другую. Пример преобразования отражением x' ₁=- x ₁, x' ₂= x ₂, x' ₃= x ₃, для которого имеем

,

показан на рис. 11.

В зависимости от закона преобразования компонент по отношению к выделенным двум классам линейно-ортогональных преобразований все тензорные величины разделяют на истинные тензоры, или просто тензоры, и псевдотензоры. Общее определение псевдотензора P _{ikl …}состоит в задании закона преобразования его компонент формулой

, (35)

где D=det||α _im || – определитель матрицы коэффициентов линейно-ортогонального преобразования координат. В тех операциях, которые не используют преобразование отражения Dº1, и закон преобразования компонент псевдотензора (35) совпадает с законом преобразования компонент истинных тензоров, даваемого формулой

.

В этой связи договоренность пользоваться в физике только правыми системами координат означает, по сути, возможность единообразного описания тензорных величин, избегая их подразделения на истинные тензоры и псевдотензоры. Следует, впрочем, заметить, что для понимания отдельных явлений (оптическая активность, магнитная гиротропия, электродинамика "леворуких" сред [4]) невозможно обойтись без сопоставления правого и левого. В этих условиях разграничение тензоров и псевдотензоров становится неизбежным.

В качестве примера псевдотензора первого ранга можно рассматривать любой аксиальный вектор, например момент силы или орбитальный момент импульса. Из аналитической геометрии также известно, что смешанное – скалярно-векторное произведение трех радиус-векторов (r ₁´ r ₂)× r ₃ определяет объем V параллепипеда, построенного на этих векторах (рис. 12). По своему смыслу V есть скаляр, но в данном случае

мы видим, что скалярное произведение образуется полярным вектором r3и аксиальным вектором в виде векторного произведения (r1´r2). Последний сомножитель будет, очевидно, чувствителен к выбору правой или левой системы координат. Соответственно закон преобразования объема, рассуждая формально строго, должен подчиняться правилу (35), т.е. иметь вид (см. также [5], стр. 123) . (36) Действительно, если r1 и r2 на рис. 12 поменять местами, то V' по отношению к V поменяет знак.

Рис. 12. Параллепипед с векторной тройкой в качестве ребер.

Таким образом, объем V является псевдотензором нулевого ранга, иначе – псевдоскаляром. В геометрии, во избежание отрицательности объемов, оговаривается, что только модуль скалярно-векторного произведения характеризует объем.

Цепочку примеров псевдотензоров замыкает специальный антисимметрический тензор третьего ранга e _ikl =(e _i ´ e _k)× e _l, компоненты которого образуются скалярно-векторным произведением ортов e ₁, e ₂, e ₃ координатных осей декартовой системы координат и называются символами Леви-Чивита. Этот псевдотензор является аналогом единичного тензора d _ik и с его помощью можно образовывать псевдотензоры различных рангов. Так, если T_ikl – истинный тензор третьего ранга, то величина P=e _iklT_ikl представляет собой псевдоскаляр, а если T_ik – истинный тензор второго ранга, то величины P _i = e _iklT_kl образуют псевдовектор, причем в случае, когда T_kl = A_kB_l, его компонентами являются компоненты векторного произведения (A ´ B). В явном виде символы Леви-Чивита определяются формулой

Алгебра псевдотензоров аналогична алгебре обычных тензоров и, как вытекает из закона преобразования (35), характеризуется (по итоговому результату) следующими особенностями:

1. произведение двух псевдотензоров является истинным тензором, ранг которого равен сумме рангов сомножителей;
2. произведение псевдотензора и истинного тензора является псевдотензором;
3. свертывание псевдотензора дает псевдотензор низшего ранга.

Уравнения механики и физики можно было бы излагать, не используя такого "подозрительного" (зависимого от избираемого типа системы координат и в этом смысле противоречащего основной идее тензорного исчисления) понятия, как псевдотензор. Это, однако, искупается бóльшей наглядностью и простотой соотношений, основанных, в частности, на представлении об аксиальных векторах. С другой стороны, не видно и логических оснований для того, чтобы в математике отказаться от операции векторного произведения векторов.

В приложениях особенно часто встречаются тензоры второго ранга, например, тензоры деформаций и упругих напряжений (теория упругости), тензор диэлектрических и магнитных проницаемостей (кристаллофизика, физика плазмы), тензоры электрической проводимости, коэффициентов диффузии, теплопроводности [2] и т.д. Одна из распространенных задач при рассмотрении свойств этих тензоров заключается в выборе системы координат, в которой они имеют наиболее простой вид. Сообразно тому, что всякому симметрическому тензору T_ik второго ранга[2] можно сопоставить геометрический образ – характеристическую или тензорную поверхность

, (37)

можно говорить о задаче определения главных осей тензорной поверхности или просто – главных осей тензора.

Задача приведения тензора к главным осям напрямую связана с определением условий, при которых вектор B, образуемый в результате скалярного умножения тензора T_ik на некоторый вектор A, не меняет своей ориентации по отношению к вектору A. Иначе говоря, если B= l A (l – скаляр), то каковым должен быть вектор A, чтобы выполнялись равенства

. (38)

В общем случае аффинных косоугольных координат величины A_i, входящие в правую часть (38), можно представить согласно второй формуле (23) в виде A_i = g_ikA^k. Поэтому вместо (38) получим равенства

. (39)

Здесь g_ik – метрический тензор, свободный индекс i задает фактически номер уравнения в системе уравнений (39), индекс k, по которому ведется суммирование, устанавливает порядковый номер члена в каждом таком уравнении.

Распишем уравнения (39) в явном виде для ортогональной системы координат, когда g_ik= d _ik и можно опустить контравариантный индекс, заменяя A^k ® A_k. С учетом свойства диагональности единичного тензора d _ik (см. формулу (25)) имеем в итоге

 

(40)

 

Выражения (40) представляют однородную систему алгебраических уравнений для определения неизвестных компонент вектора A= (A ₁, A ₂, A ₃). Нетривиальное (A ¹0) решение системы (40), как известно [1], существует, если определитель системы равен нулю. Таким образом, получим уравнение

 

, (41)

 

которое называется характеристическим уравнением тензора T_ik. Нетрудно видеть, что оно является кубическим по параметру l и определяет в общем случае три различных корня l_1,2,3, представляющие собой главные (собственные) значения тензора.

При подстановке каждого из найденных главных значений тензора l_s в систему уравнений (40) искомые величины A_i в ней мы должны снабдить соответствующим номером s, который для отличия от тензорных индексов условимся писать сверху и заключать в круглые скобки. Это означает, что определяемые величины A_i ^{( s )} относятся только к избранному главному значению тензора. Таким образом, удается определить вектор A ^{( s )}, ставящий в соответствие этому главному значению определенное направление, которое называется главной осью тензора.

Следует подчеркнуть, что система уравнений (40) позволяя установить связи (отношения) между компонентами вектора A ^{( s )} в виде

 

, (42)

 

однозначно определяет только направление этого вектора. Неопределенность самой величины (длины) вектора обуславливается тем, что одну из его компонент, например A ₁^{( s )}, приходится выбирать по произволу, тогда как остальные пересчитываются через нее по формулам (42).

Определение главной оси тензора возможно только при вещественном значении l _s. Наиболее просто обстоит дело с вещественностью корней характеристического уравнения (41) в случае симметричного тензора. В линейной алгебре [1] для системы уравнений (40) с симметричным тензором T_ik имеется строгое доказательство того, что все три корня существуют и они вещественны. Следовательно, любой симметричный тензор T_ik имеет три главных оси, причем, как показывают уравнения (40) (доказательство см. в [5]), они взаимно перпендикулярны. Примечательно, что возможная кратность корней характеристического уравнения (41) не оказывает влияния ни на число главных осей тензора, ни на их взаимную ортогональность.

Из-за взаимной ортогональности главные оси тензора можно рассматривать в качестве осей новой системы координат x'_i. Тогда, определяя коэффициенты преобразования a _im для перехода в эту систему из некоторой исходной системы координат x_m, в соответствии с законом преобразования тензора T'_ik =a _im a _knT_mn можно показать, что в системе координат своих главных осей тензор примет вид

 

. (43)

 

При этом тензорная поверхность (37) для симметричного тензора имеет характерный вид эллипсоида (тензорный эллипсоид), вытянутого вдоль главной оси наименьшего главного значения (рис. 13) и отсекающего по координатны

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: