Дифференцирование тензоров.

В приложениях любая тензорная величина (условимся представлять ее тензором второго ранга T_ik) призвана характеризовать вполне определенное качество физической системы. Это может быть материальная характеристика среды, например, показатель преломления, или параметр, выражающий эффективность некоторого взаимодействия между частицами (частями) системы. Наконец, рассматривая поведение физической системы под внешним воздействием, соответствующему тензору целесообразно придавать смысл меры отклика системы на внешнее воздействие.

Существенно, что при любых попытках описания физической системы мы не вправе игнорировать ее пространственную протяженность и геометрическую конфигурацию слагающих частей. Точно также, само существование физической системы мы обязаны подразумевать как некий процесс, развивающийся (быстро, медленно или бесконечно медленно, применительно к "застывшим" состояниям системы) во времени t. Таким образом, становится очевидным, что помимо прочих возможных требований и условий соответствующую тензорную величину следует обязательно рассматривать как функцию радиус-вектора r точек системы и времени t. Данное обстоятельство можно математически выразить в виде равенств

 

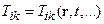, i,k =1,2,3, (46)

 

где область многоточий резервируются под аргументы (скаляры, векторы или тензоры), которыми характеризуются дополнительные связи, налагаемые на рассматриваемую тензорную величину конкретикой задачи.

Функциональные соотношения (46) представляют тензор-функцию вектора r, скаляра t и других аргументов, о которой говорят, что она задает тензорное поле T_ik в области состояний системы. В простейшем случае, когда система пространственно однородна, ее поведение во всех точках будет одинаковым и изучение системы можно свести к определению ее характеристик в отдельно взятой точке r=R ₀ºconst. Тогда, абстрагируясь от разного рода внешний влияний и связей вместо (46) получим тензор-функцию от скалярного аргумента

 

. (47)

 

Каждую из компонент тензора (47) можно рассматривать независимо от других как обычную функцию скалярного аргумента t. Соответственно, производную тензора по этому аргументу можно рассматривать как совокупность производных всех его компонент

 

. (48)

 

Иными словами, правила дифференцирования тензоров скалярного аргумента более высокого ранга, чем векторы, ничем не отличаются от правил дифференцирования векторов. Единственная требующаяся оговорка касается лишь того ограничения, что дифференциируемый тензор должен рассматриваться в не изменяющейся системе координат, т.е. системе координат, не зависящей от t. При этом мы подразумеваем, что область существования нового тензора V_ik совпадает с областью существования исходного тензора T_ik за вычетом всех интервалов аргумента t, в которых нарушаются условия существования производных всех отдельных функций. Согласно определению производной тензора по скалярному аргументу формулой (48) видно, что дифференциирование тензора по скалярному аргументу не меняет его ранг.

Наряду с тензор-функциями скалярного аргумента типа (47) большое место в приложениях занимают тензор-функции векторного аргумента

 

. (49)

 

Этот класс тензорных полей описывает установившееся (стационарное) состояние системы, начиная с некоторого момента времени t ₀, и представляет собой обобщение понятий скалярных и векторных полей классической физики, например, скалярного поля давления в атмосфере p = p (r) или электростатического потенциала j=j(r), векторного поля электрической напряженности E = E (r) и т.д. Простейшим случаем стационарного тензорного поля (49) является поле упругих напряжений T_ik, возникающих при деформировании упругой среды под действием внешних статических сил.

Основные ограничения, налагаемые на тензорные поля (49), заключаются в выполнении условий их пространственной непрерывности и однозначности, которые применительно к реальным физическим системам всегда выполняются. Математически это означает, что векторные функции, составляющие в своей совокупности тензор-функцию векторного аргумента, должны быть непрерывными и однозначными в общей области их определения. Очевидно, что все операции, производимые над тензорами, распространяются и на тензор-функцию при том единственном условии, что производятся в каждой точке поля. Так, сложение двух тензорных полей (по условию выполнения этой операции тензоры слагаемых полей должны иметь одинаковый ранг и одинаковую физическую размерность) приводит в каждой точке пространства к новому, суммарному тензорному полю того же ранга, тензор которого в каждой точке является суммой исходных тензоров в этой точке.

Поскольку точка пространства задается радиус-вектором, то, по сути, представление тензорного поля (49) будет неявным образом привязано к системе координат, которая используется для определения радиус-вектора. Поэтому при преобразованиях тензорного поля к новому базису наряду с самим тензором соответствующее преобразование будет претерпевать радиус-вектор – аргумент векторных функций, слагающих тензор поля в каждой точке.

Пространственная непрерывность тензорного поля подразумевает возможность дифференцирования тензор-функции вида (49). В отличие от случая тензор-функции скалярного аргумента (47) эта процедура имеет более сложный характер. Во-первых, требуется указать координату, по которой будет осуществляться дифференциирование, или определить комбинацию всего комплекса производных, выражающую то, что может быть названо производной тензора по радиус-вектору. Во-вторых, если пределы типа частных производных

 

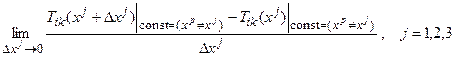(50)

 

существуют, то при этом предельном переходе базис системы координат должен оставаться постоянным. В-третьих, в выражении (50) контрвариантный (нумерует координаты) верхний индекс j выступает по отношению к тензорным индексам i и k как независимый (свободный). Следовательно, величины, образуемые предельным переходом по способу, указываемому формулой (50), будут уже зависеть не от двух (исходных) индексов i, k, а от трех – i, k, j.

В тензорном анализе [5] показано, что величины

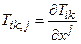, , (51)

образуемые в результате дифференцирования компонент ковариантного и контравариантного тензоров также составляют тензоры, но уже более высокого, на единицу большего третьего ранга. При этом выражения (51) имеют силу только в прямоугольных декартовых координатах, так как только в них удается соблюсти требование неизменности базиса в предельных переходах типа (50). Иллюстрацией сказанному служит рис. 15, на котором показаны плоскостные локальные базисы (базисы системы координат в точках определения тензорного поля) для некоторых двух близко расположенных точек I и II. В левой части рисунка картина дана для случая прямоугольной декартовой системы координат. В правой же стороне построение выполнено при выборе полярной системы координат. Несмотря на то, что ортогональность единичных векторов e _r и e _q в полярных координатах соблюдается, как и в декартовых, в каждой точки плоскости, видно, что переход от точки I к точке II вдоль штриховой кривой сопровождается поворотом локального базиса. В декартовых координатах (слева) такой переход не сопровождается поворотом (и, следовательно, изменением) локального базиса тензорного поля.

 

Рис. 15. Локальные базисы тензорного поля в декартовой (слева) и полярной (справа) системах координат

Обобщение формул (51) на случай произвольной системы координат проще всего продемонстрировать на примере векторного поля. Рассмотрим некоторый вектор A в системе координат x ¹, x ², x ³ с локальным базисом (e ₁, e ₂, e ₃), если вектор контравариантный и (e ¹, e ², e ³) – если он ковариантный. Каждый из векторов e _i или e ⁱ является вектор функцией координат, т.е. e _i = e _i (x ¹, x ², x ³), e ⁱ = e ⁱ (x ¹, x ², x ³). На этом основании напишем d A = d (A_k e ^k)= dA_k e ^k + A_kd e ^k, d A = d (A^l e _l)= dA^l e _l + A^ld e _l Вторые слагаемые здесь характеризуют изменение векторного поля в связи с изменением локального базиса при переходе от точки к точке.

В основных координатах и соответственно тому, что A= A^k e _k = A_k e ^k, напишем

(52)

 

Рассмотрим далее величины и . Первые из них представляют совокупность ковариантных[3] компонент векторов ¶ A /¶ x^m (это не один вектор, так как m =1,2,3) и образуют ковариантную производную ковариантного вектора.

Вторые величины представляют уже контравариантные компоненты указанных векторов – иначе говоря, образуют уже ковариантную производную контравариантного вектора.

Для явного представления A_{k ; m} воспользуемся второй из формул (52). В образующемся равенстве

немой индекс k в величинах, заключенных в скобки, мы вправе заменить любым другим, например j. Поэтому получим

.

Произведение (e ^j × e _k) – есть по аналогии с выражениями (24) метрический тензор g^j_k, который для ортогонального базиса аналогично (25) является единичным тензором. В таком случае очевидно, что

. (53)

Заметим также, что производная в силу постоянства компонент единичного тензора d ^j_k всегда тождественно равна нулю, т.е. . Второе слагаемое в выражении для A_{k ; m} можно тогда преобразовать к виду

,

где обозначенные как

(54)

величины (их всего 27 в трехмерном пространстве), называются символами Кристоффеля.

С учетом формул (53), (54) получим

. (55)

Аналогичным образом, привлекая первую из формул (52), можно сконструировать выражение

, (56)

определяющее ковариантную производную от контравариантного вектора. Формулы (55), (56) показывают, что ковариантная производная векторного поля учитывает не только изменения самого поля при перемещении вдоль координатных линий (первые слагаемые), но и изменения локального базиса (вторые члены). Как следствие того, что вторые члены выражений (55), (56) обязаны своим происхождением введению местного, подвижного координатного базиса, символы Кристоффеля должны выражаться через производные от компонент метрического тензора. Именно, можно показать [5], что если g^ik и g_ik – компоненты метрического тензора взаимного и исходного локального базисов, то

 

. (57)

 

Сами по себе символы Кристоффеля не образуют тензора. Однако их посредством осуществляется операция ковариантного дифференцирования вектора, превращающая его из тензора первого ранга в тензор второго ранга.

Формулы (55), (56) легко обобщаются на случай тензора второго ранга. Для этого в них на место компонент вектора A следует подставить компоненты соответствующего тензора T_ik или T^ik. Следует только помнить, что во вторых слагаемых формул (55), (56) свертка с символами Кристоффеля осуществляется только по одному индексу. Поэтому немыми должны стать поочередно вначале первый, а затем второй тензорные индексы и соответственно вторые члены уравнений (55), (56) подвергнутся следующим преобразованиям:

.

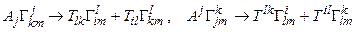В результате формулы ковариантного дифференцирования тензора второго ранга примут вид

(58)

 

К ним остается добавить формулу ковариантного дифференцирования смешанного тензора второго ранга T ⁱ_k, которая запишется следующим образом

. (59)

 

 

 

 

ЛИТЕРАТУРА

 

1. В.А.Ильин, Э.Г.Поздняк. Линейная алгебра. М.: Наука, 1978. 304 с.
2. Дж. Най. Физические свойства кристаллов. М.: Мир, 1967. 388 с.
3. А.М.Косевич. Основы механики кристаллической решетки. М.: Наука, 1972. 280 с.
4. В.Г.Веселаго. Электродинамика материалов с отрицательным коэффициентом преломления // УФН. 2003. Т. 173. № 7. С. 790-794.
5. А.И.Борисенко, И.Е.Тарапов. Векторный анализ и начала тензорного исчисления. М.: Высшая школа, 1966. 252 с.

* Здесь мы сталкиваемся с необходимостью принципиально иного обозначения (нумерации) векторов взаимного базиса, для чего поднимаем индексы вверх. Было бы, например, ошибкой применить для векторов взаимного базиса обозначение типа (e '₁ ,e '₂, e '₃) со старым размещением индексов, поскольку это значило просто переход к другой (штрихованной) аффинной системе координат без качественного преобразования структуры базиса. Как пример качественных изменений векторных величин при переходе от одного класса базисов к другому можно, чисто формально, указать на вектор с компонентами, представленными матрицей-столбцом и матрицей-строкой.

* Мы могли бы, например, записывать контравариантные компоненты векторов строчными латинскими буквами, а ковариантные – заглавными, или же обозначать последние готическим шрифтом.

[1] Инвариант здесь понимается как величина, сохраняющая свое значение при оговоренном типе преобразования координат.

[2] Почти все тензорные величины, встречающиеся в физике и механике, этому требованию удовлетворяют.

[3] Получаются в результате умножения на векторы обратного базиса e _k и, соответственно, пишутся с нижними индексами.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: