 |
Суть стохастической модели
|
|
|
|
ДЕТЕРМИНИРОВАННЫЕ И СТОХАСТИЧЕСКИЕ
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Постановка задачи
Детерминированные модели описывают процессы в детерминированных системах.
Детерминированные системы характеризуются однозначным соответствием (соотношением) между входными и выходными сигналами (процессами).
Если задан входной сигнал такой системы, известны ее характеристика y = F(x), а также ее состояние в начальный момент времени, то значение сигнала на выходе системы в любой момент времени определяется однозначно (рис. 2.1).
Существует два подхода к исследованию физических систем: детерминированный и стохастический.
Детерминированный подход основан на применении детерминированной математической модели физической системы.
Стохастический подход подразумевает использование стохастической математической модели физической системы.
Случайные факторы (шумы)
Внутренние факторы −
1) температурная и временная нестабильность электронныхкомпонентов;
2) нестабильность питающего напряжения;
3) шум квантования в цифровых системах;
4) шумы в полупроводниковых приборах в результате неравномерности процессов генерации и рекомбинации основных носителей заряда;
5) тепловой шум в проводниках за счет теплового хаотического движения носителей заряда;
6) дробовой шум в полупроводниках, обусловленный случайным характером процесса преодоления носителями потенциального барьера;
7) фликкер – шум, обусловленный медленными случайными флуктуациями физико-химического состояния отдельных областей материалов электронных устройств и т. д.
|
|
|
Внешние факторы –
1) внешние электрические и магнитные поля;
2) электромагнитные бури;
3) помехи, связанные с работой промышленности и транспорта;
4) вибрации;
5) влияние космических лучей, тепловое излучение окружающих объектов;
6) колебания температуры, давления, влажности воздуха;
7) запыленность воздуха и т. д.
Влияние (наличие) случайных факторов приводит к одной из ситуаций, приведенных на рис. 2.2:
 |
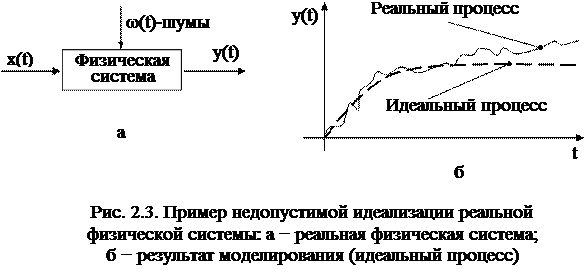
Следовательно, предположение о детерминированном характере физической системы и описание ее детерминированной математической моделью является идеализацией реальной системы. Фактически имеем ситуацию, изображенную на рис. 2.3.
Детерминированная модель допустима в следующих случаях:
1) влияние случайных факторов столь незначительно, что пренебрежение ими не приведет к ощутимому искажению результатов моделирования.
2) детерминированная математическая модель отображает реальные физические процессы в усредненном смысле.
В тех задачах, где не требуется высокой точности результатов моделирования, предпочтение отдается детерминированной модели. Это объясняется тем, что реализация и анализ детерминированной математической модели много проще, чем стохастической.
Детерминированная модель недопустима в следующих ситуациях: случайные процессы ω(t) соизмеримы с детерминированными x(t). Результаты, полученные с помощью детерминированной математической модели, будут неадекватными реальным процессам. Это относится к системам радиолокации, к системам наведения и управления летательными аппаратами, к системам связи, телевидению, к системам навигации, к любым системам, работающим со слабыми сигналами, в электронных устройствах контроля, в прецизионных измерительных устройствах и т. д.
|
|
|
В математическом моделировании случайный процесс часто рассматривают как случайную функцию времени, мгновенные значения которой являются случайными величинами.
Суть стохастической модели
Стохастическая математическая модель устанавливает вероятностные соотношения между входом и выходом системы. Такая модель позволяет сделать статистические выводы о некоторых вероятностных характеристиках исследуемого процесса y(t):
1) математическое ожидание (среднее значение):
(2.1)
2) дисперсия (мера рассеивания значений случайного процесса y(t) относительно его среднего значения):
(2.2)
3) среднее квадратичное отклонение:
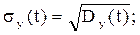(2.3)
4) корреляционная функция (характеризует степень зависимости – корреляции – между значениями процесса y(t), отстоящими друг от друга на время τ):
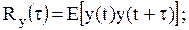(2.4)
5) спектральная плотность случайного процесса y(t) описывает его частотные свойства:
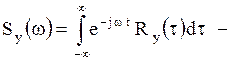(2.5)
преобразование Фурье.
Стохастическаямодель формируется на основе стохастического дифференциального либо стохастического разностного уравнения.
Различают три типа стохастических дифференциальных уравнений: со случайными параметрами, со случайными начальными условиями, со случайным входным процессом (случайной правой частью). Приведем пример стохастического дифференциального уравнения третьего типа:
, (2.6)
где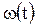 
– аддитивный случайный процесс – входной шум.
В нелинейных системах присутствуют мультипликативные шумы [x(t)·μ(t)].
Анализ стохастических моделей требует использования довольно сложного математического аппарата, особенно для нелинейных систем.
|
|
|
